蜗轮齿轮公差计算应用案例

[例] 已知蜗杆传动ZN10×90RZ/80，精度等级为传动7fGB/T 10089—1988，确定其蜗杆、蜗轮及传动的各项公差和极限偏差的步骤如下：

第一步，按蜗杆的端面模数m_t=10mm，分度圆直径d₁=90mm，得齿顶圆直径d_a1=d₁+2m_t=110mm。按蜗轮的端面模数m_t=10mm，齿数Z₂=80，得分度圆直径d₂=Z₂m_t=800mm；齿宽Z₁≤3时，b=0.75d_a1=82.5mm。中心距a=（90+800）/2mm=445mm。

第二步，确定蜗杆的公差或极限偏差。先按m_t＞6.3～10mm，精度等级为7级，查表8-13，得螺旋线公差f_h1=50μm、一转螺旋线公差f_h=25μm、轴向齿距极限偏差±f_px=±17μm、轴向齿距螺积公差f_px1=32μm、齿形公差f_f1=28μm。再按d₁＞80～125mm，m_t≥1～16，查表8-14得齿槽径向跳动公差f_r=20μm。根据齿厚上偏差E_SS1=-（j_nmin/cosα_n+E_SΔ），查表8-27，按α＞400～500mm，侧隙种类为f，得传动最小法向间隙j_nmin=40μm；再取齿形角α_n=20°，则cos20°=0.93969；并由表8-29查得齿厚上偏差中的误差补偿部分E_SΔ=95μm，于是，E_SS1=-（40/0.93969+95）μm=-138μm。然后，查表8-28得齿厚公差T_S1=71μm，最后得齿厚下偏差E_Si1=E_SS1-T_S1=-209μm。

第三步，确定蜗轮的公差或极限偏差。先按切向综合公差F′_i=F_p+f_f2，并取分度圆弧长L=πm_tZ₂/21256.6mm，查表8-15得F_p=140μm；再按d₂＞400～800mm，m_t＞6.3～10mm，查表8-20得f_f2=24μm。于是，得F′_i=（140+24）μm=164μm。然后，查表8-17得径向综合公差F″_i=112μm；查表8-15得齿距累积公差F_p=140μm；查表8-16得齿圈径向跳动公差F_r=80μm；查表8-19得f_pt=25μm，查表8-20得f_f2=24μm，于是，一齿切向综合公差f′_i=0.6×（f_pt+f_f2）=29μm；查表8-18得一齿径向综合公差f″_i=32μm；查表8-19得，齿距极限偏差±f_pt=±25μm；查表8-20得齿形公差f_f2=24μm；齿厚极限偏差E_Si2=E_SS2-T_S2，因E_SS2=0，查表8-30得齿厚公差T_S2=130μm，故E_Si2=-130μm。

第四步，确定传动的公差或极限偏差。先按传动切向综合公差F′_ic=F_p+f′_ic，其中f′_ic=0.7（f′_i+f_h），按次查表8-15得F_p=140μm，并由已知F′_i=29μm，查表8-13得f_h=25μm，则F′_ic=（140+38）μm=178μm；传动一齿切向综合公差f′_ic=38μm；查表8-21得接触斑点接触面积的百分比，即沿齿高不小于55%，沿齿长不小于50%，且接触斑点痕迹应偏于啮出端，但不允许在齿顶和啮入、啮出端的棱边接触；按a＞400～500mm，查表8-22得中心距极限偏差±f_a=±78μm，查表8-24得中间平面极限偏差，±f_x=±63μm；按b₂＞80～120mm，查表8-61得轴交角极限偏差±f_∑=±19μm；查表8-27得最小法向侧隙j_nmin=40μm。(www.xing528.com)

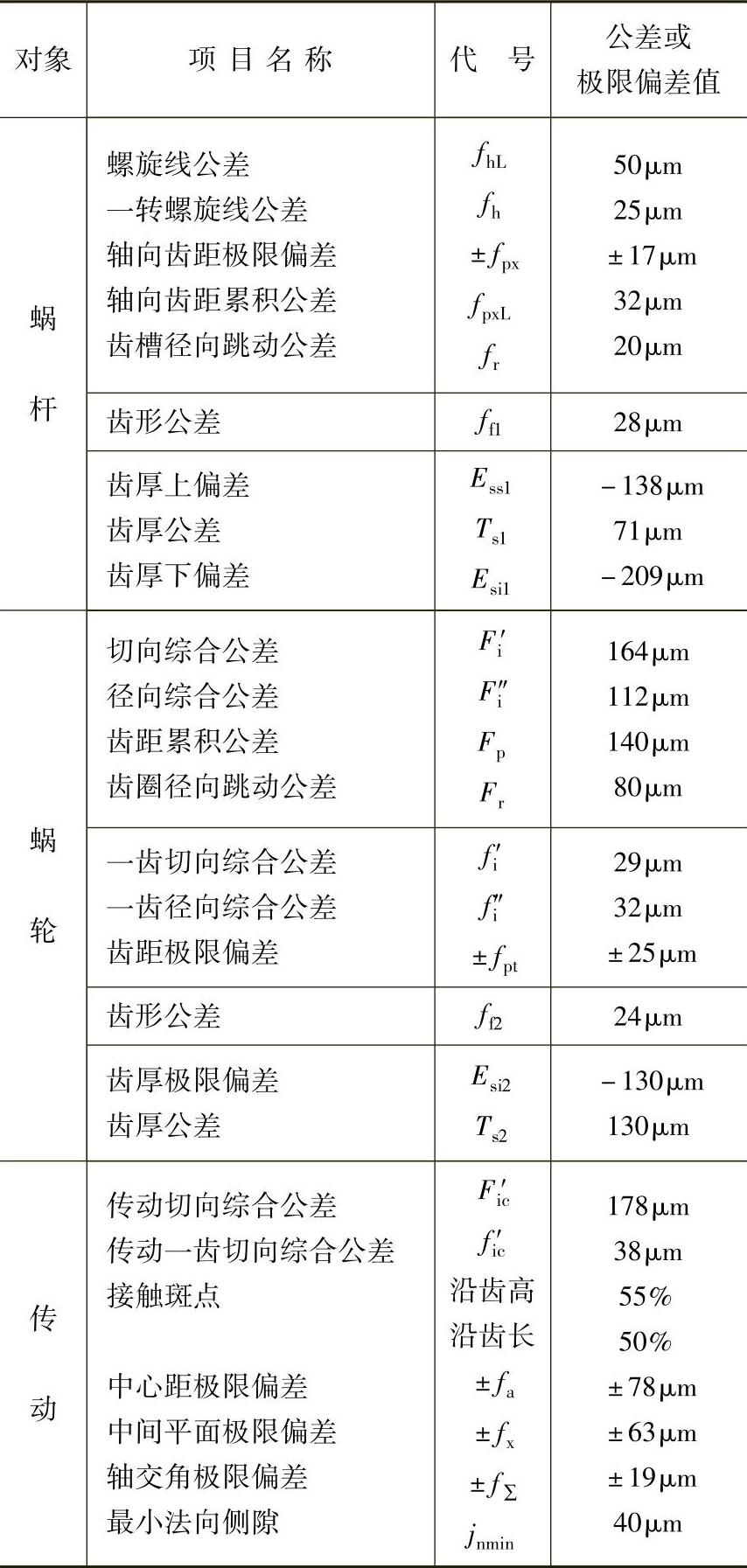
本例中蜗杆、蜗轮及蜗杆传动各项目的公差或极限偏差值如表8-36所示。

表8-36 应用示例的公差或极限偏差