基于正态分布的统计过程控制中标准差的置信区间

（1）统计参数的点估计：

1）过程能力指数C_p的点估计值：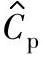

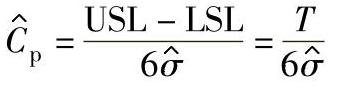
式中标准差点估计值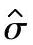可根据数据来源的控制图种类按下列三种表示方式之一计算

a.标准差的估计值基于不分组的数据。

统计过程控制中当样本大小n=1时，属于该情形。标准差的估计值用S或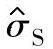表示：

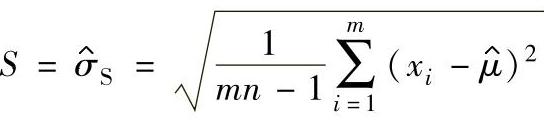
式中 n——子组大小；

mn——总观测值的数量；

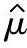——过程均值的估计值。

当采用来自控制图的数据且过程处于受控状态时，过程均值的估计值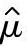可以用各子组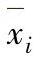均值的平均值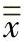表示：

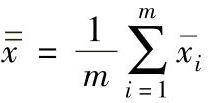
式中 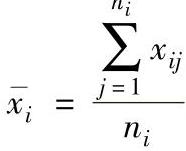，i=l，2，…，m，m为子组数。

b.标准差的估计值基于均值-标准差控制图的数据。

标准差的估计值用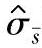表示：

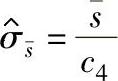
式中 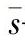——子组标准差的平均值；

c₄——和样本大小相关的系数（参见表1-129）。

c.标准差的估计值基于均值-极差控制图的数据

标准差的估计值用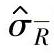表示：

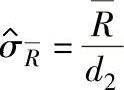
式中 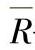——子组极差的平均值；

d₂——和样本大小相关的系数（参见表1-130）。

2）过程偏移相关参数k的点估计值。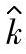

如果用总体均值的估计值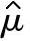（或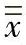）替代k的公式中的理论值μ，得到的估计值（或点估计）：

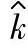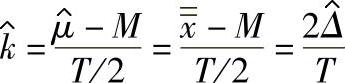
式中 M——公差带中心值；

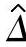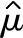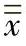——总体均值的估计值（或）对M的

偏移。

（2）基于给定置信水平的统计参数的置信区间：

1）基于给定置信水平100（1-α）%的过程均值μ的置信区间：

a.标准差已知情形。以一定的置信概率1-α得到总体均值μ的置信区间如下：

双侧100（1-α）%置信区间：

式中 z_α/2——标准正态分布的右侧α/2分位点。

单侧100（1-α）%置信区间下限μ_{1-α（min）}：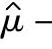

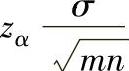
单侧100（1-α）%置信区间上限μ_{1-α（max）}：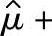

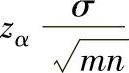
b.标准差未知情形。以一定的置信概率1-α得到总体均值μ的置信区间如下：

双侧100（1-α）%置信区间：

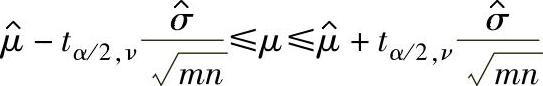
式中 ν——t分布的自由度；

t_α/2，ν——t分布的右侧α/2分位数。

单侧100（1-α）%置信区间下限μ_1-α（min）：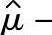

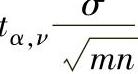
单侧100（1-α）%置信区间上限μ_1-α（max）：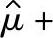

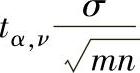
2）基于给定置信水平100（1-α）%的过程标准差σ的单侧置信区间：统计过程控制中，过程标准差σ是过程波动的度量，越小越好，通常更关注单侧100（1-α）%置信区间上限。

当过程应用统计过程控制，质量特性值服从正态分布，标准差的估计值用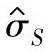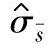，和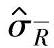分别表示时，基于1-α置信概率的标准差σ的单侧置信区间上限有三种表示方式。

a.标准差的估计值用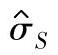表示时σ的100（1-α）%置信区间上限：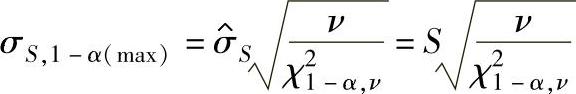

式中 ν=mn-1——χ²（ν）分布自由度；

χ²_1-α，ν——χ²（ν）分布的1-α分位数。

b.标准差的估计值用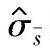表示时σ的100（1-α）%置信区间上限：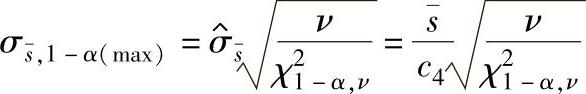

式中 ν=f_nm（n-1）——χ²（ν）分布自由度；

m——样本个数；

n——样本大小（容量）；

c₄——和样本大小相关的系数。

f_n和c₄数值见表1-128和表1-129。

表1-128 系数f_n数值表

表1-129 系数c₄数值表

c.标准差的估计值用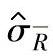表示时σ的100（1-α）%置信区间上限：

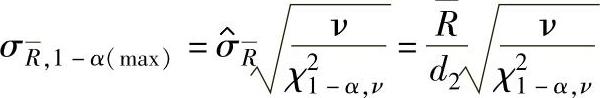
式中 ν=0.9m（n-1）——χ²（ν）分布自由度；

d₂——和样本大小相关的系数，数值见表1-130。(https://www.xing528.com)

表1-130 系数d₂数值表

3）基于给定置信水平100（1-α）%的过程能力指数C_p的置信区间

a.C_p的双侧100（1-α）%置信区间：

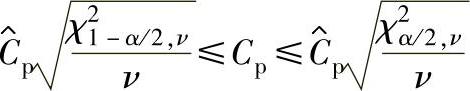
式中 χ²_1-α/2，ν和χ²_α/2，ν——分别为具有自由度ν的χ²分布的下侧α/2分位点和上侧α/2分位点。

自由度ν由计算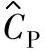时的标准偏差σ的估计值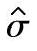确定，分别为：

对于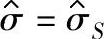，ν=mn-1；对于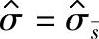，ν=f_nm（n-1）；对于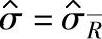，ν=0.9m（n-1）。

b.C_p的单侧100（1-α）%置信区间下限C_{p，1-α（min）}。

为了保证过程满足某个C_p目标值，C_p的实际值应大于等于C_p目标值。所以，应主要考虑单侧100（1-α）%置信区间的下限C_{p，1-α（min）}，计算公式如下：

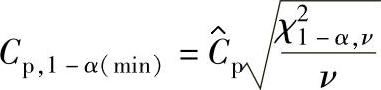
式中 χ²_1-α，ν——χ²分布的分位数。

自由度ν取值方法与上述a相同。

4）基于给定置信水平100（1-α）%的过程偏移参数k的置信区间：

a.k的双侧100（1-α）%置信区间：C_p已知时，偏移参数k的双侧100（1-α）%置信区间为：

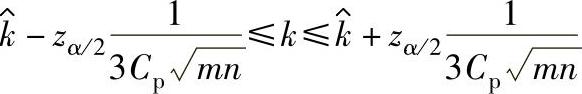
C_p未知时，偏移参数k的双侧100（1-α）%置信区间为：

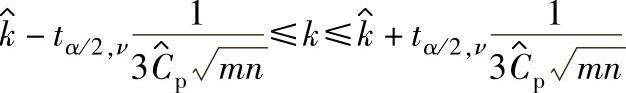
b.k的单侧100（1-α）%置信区间：用k_U，1-α表示k的单侧100（1-α）%置信区间上限，k_L，1-α表示k的单侧100（1-α）%置信区间下限，表1-131和表1-132给出k为正、负值时的单侧100（1-α）%置信区间上、下限。

表1-131 k为正值时的单侧100（1-α）%置信区间

表1-132 k为负值时的单侧100（1-α）%置信区间

对于偏移参数k，其绝对值越小越好，应主要考虑置信区间绝对值偏大方向的界限。即k为正值时其单侧置信区间上限和k为负值时的单侧置信区间下限。二者可统一为k_U，1-α。

C_p已知时，k的单侧100（1-α）%置信区间上限：

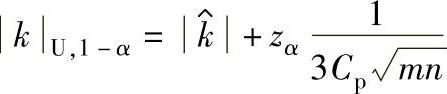
C_p未知时，k的单侧100（1-α）%置信区间上限：

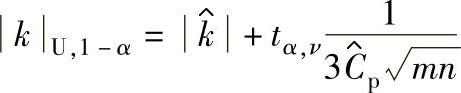
5）C_pk的100（1-α）%置信区间：

a.C_pk的双侧100（1-α）%置信区间：

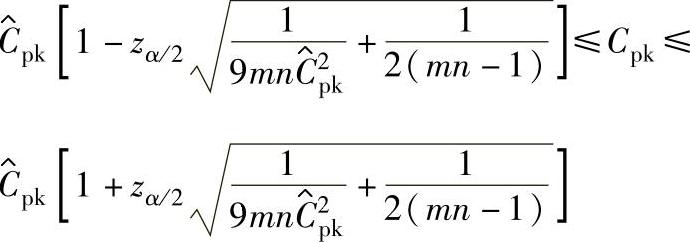
b.C_pk的单侧100（1-α）%置信区间下限C_{pk，1-α（min）}：为了保证过程满足某个C_pk目标值，C_pk的实际值应大于等于C_pk目标值。所以，应主要考虑单侧100（1-α）%置信区间的下限C_{pk，1-α（min）}，计算公式如下：

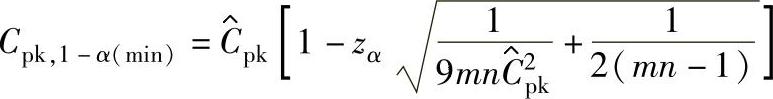
（3）估计值的统计公差：

1）基于给定置信水平100（1-α）%的标准差估计值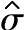的统计公差：

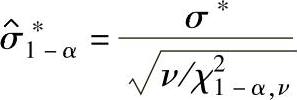
式中 σ^∗——预先设定的标准偏差的统计公差。

2）基于给定置信水平100（1-α）%的过程能力指数估计值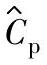的统计公差：根据质量目标确定的统计公差是以理论值的形式给出过程能力指数C^∗_p。当采用抽样数据以估计值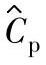评价过程能力时，以置信概率1-α满足C_p≥C^∗_p的估计值的统计公差用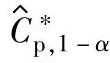表示：

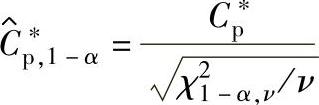
3）基于给定置信水平100（1-α）%的过程偏移相关参数估计值的统计公差：以给定置信水平100（1-α）%满足∣k∣≤k^∗的估计值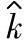的统计公差。

根据质量目标确定的统计公差是以理论值的形式给出过程偏移系数控制界限值k^∗。当采用抽样数据以估计值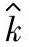评价过程偏移，以置信概率1-α满足控制条件∣k∣≤k^∗时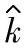，的统计公差为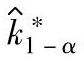，且：

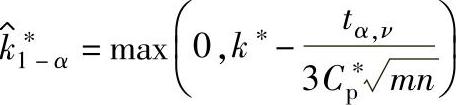
4）特定条件下估计值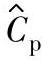和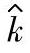的统计公差表（见表1-333和表1-134）。

为简化估计值的统计公差设定并为选择合适的子组大小n及子组个数m提供参考，按照12.4.3节的推荐α=0.1，即置信水平按90%给定。表1-133给出基于给定置信水平90%的过程能力指数估计值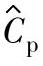的统计公差表。

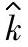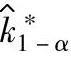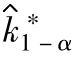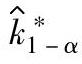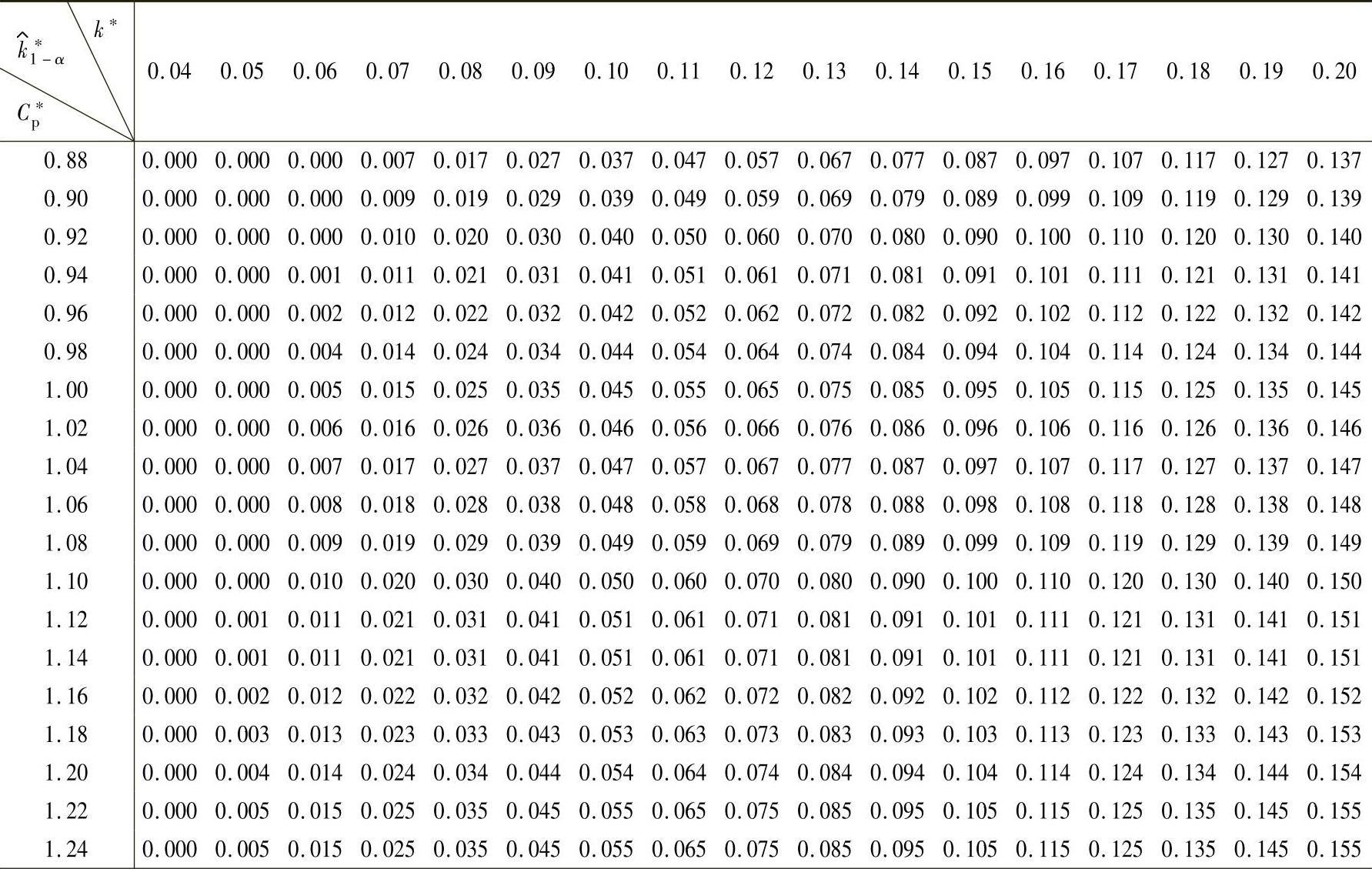
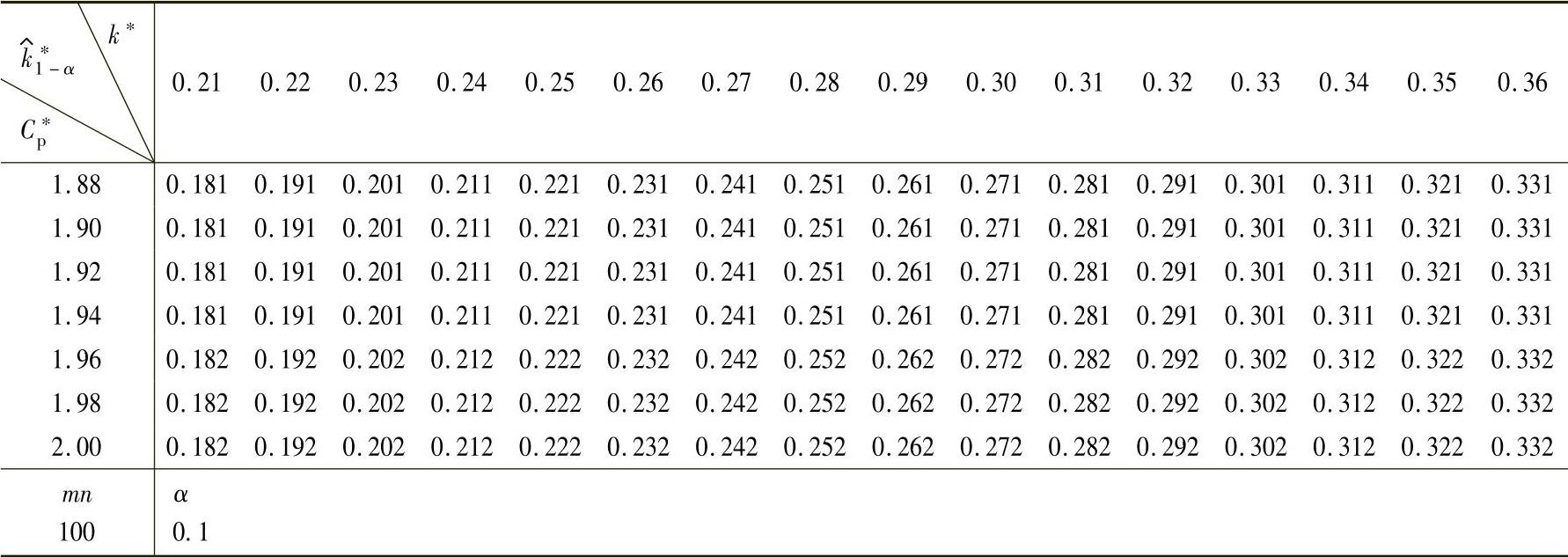
的统计公差取决于4个变量，即C^∗_p，k^∗，α和mn组合（自由度ν和总数据数N均由mn组合确定）。为简化计算，方便应用，推荐N=mn=100，α=0.1，自由度ν按N-1=99代入的计算公式，则仅取决于2个变量，即C^∗_p，k^∗。表1-134给出基于给定置信水平90%，mn=100的过程偏移参数估计值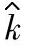的统计公差表。

表1-133 基于给定置信水平90%的过程能力指数估计值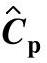的统计公差表

（续）

（续）

（续）

表1-134 基于给定置信水平90%，mn=100的过程偏移参数估计值k的统计公差表（以预定置信度及C_p计算k的估计值的统计公差表）

（续）

（续）

（续）