评估误判率对验收质量的影响

在GB/T 3177—2009的资料性附录中，提供了误判概率与验收质量的评估资料，对两种验收极限分别就验收工件时的误判概率，以工件尺寸遵循正态分布、偏态分布和均匀分布三种情况进行了分析和计算。

按验收原则规定，所用验收方法应只接收位于规定尺寸极限之内的工件。但是，由于计量器具和测量系统都存在误差，任何测量方法都可能发生一定的误判概率。因此应阐明由测量误差引起的误判概率的计算，并引用误判概率的大小来评估验收质量的高低。

（1）误判概率的计算

1）基本概念：验收工件时发生的误判有两类：误收与误废。误收是指把尺寸超出规定尺寸极限的工件判为合格；误废是指把处在规定尺寸极限之内的工件判为废品。误收影响产品质量，误废造成经济损失。误收概率（以下简称误收率）或误废概率（以下简称误废率）统称误判概率。

2）计算公式：

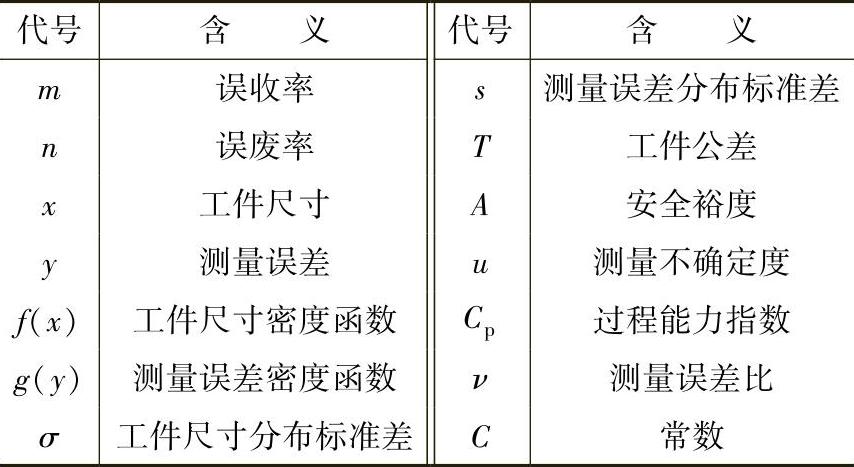
a.代号。见表1-23。

表1-23 计算公式的代号

b.公式。参看图1-36。

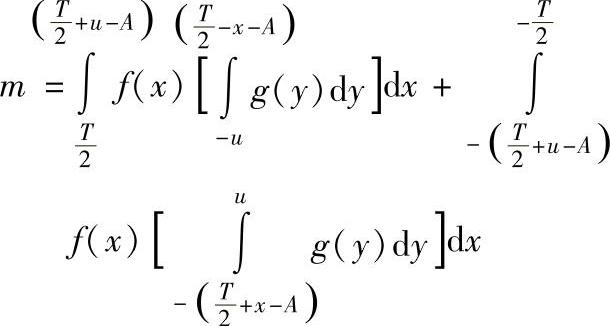
（等号右端第1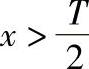项，第2项）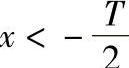

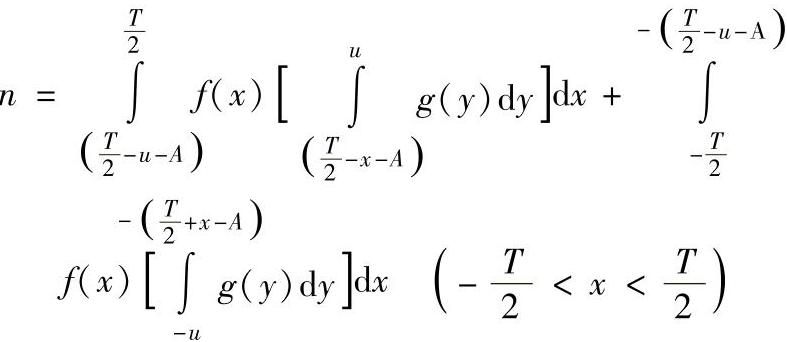
当f（x）为对称型分布函数时，以上二式可以简化为：

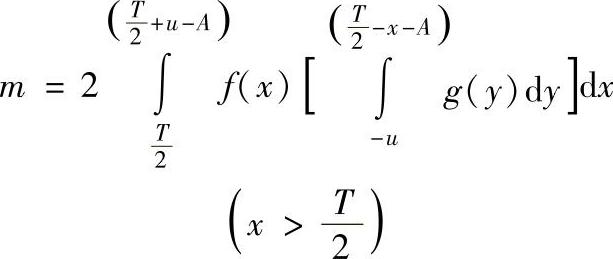
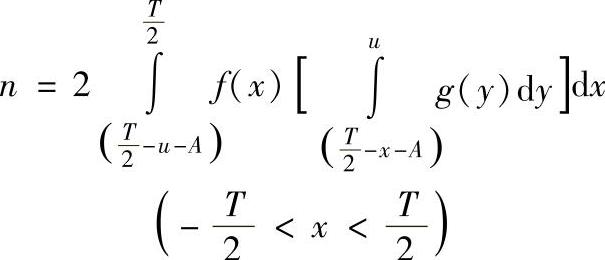
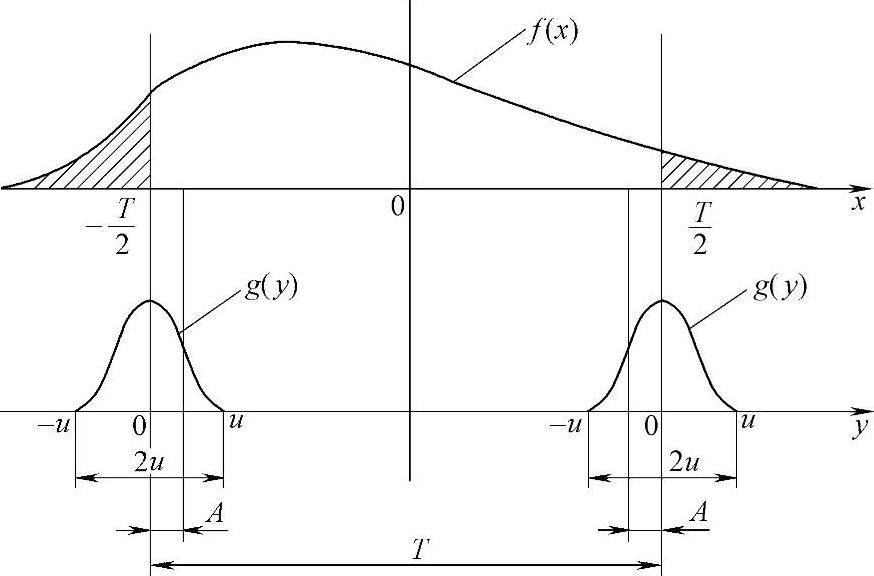
图1-36 工件尺寸与测量误差

3）决定误判概率的条件：由计算公式可见，m与n决定于x与y的分布形式及其积分界限。这里工件公差T以工件尺寸分布标准差σ为单位，测量不确定度u以测量误差分布标准差s为单位。引入过程能力指数C_p=T/Cσ，测量误差比ν=2u/T，于是误收率m与误废率n值决定于：f（x）、C_p、g（y）、ν及A。其中f（x）与C_p决定于过程条件，g（y）与ν决定于测量条件，A决定验收极限。

（2）按方式B决定验收极限验收工件时的误判概率：

1）工件尺寸遵循正态分布：验收极限按方式B决定，即A=0。工件尺寸遵循正态分布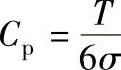，；测量误差遵循正态分布并取u=2s。这时m与n值见图1-37及表1-24。

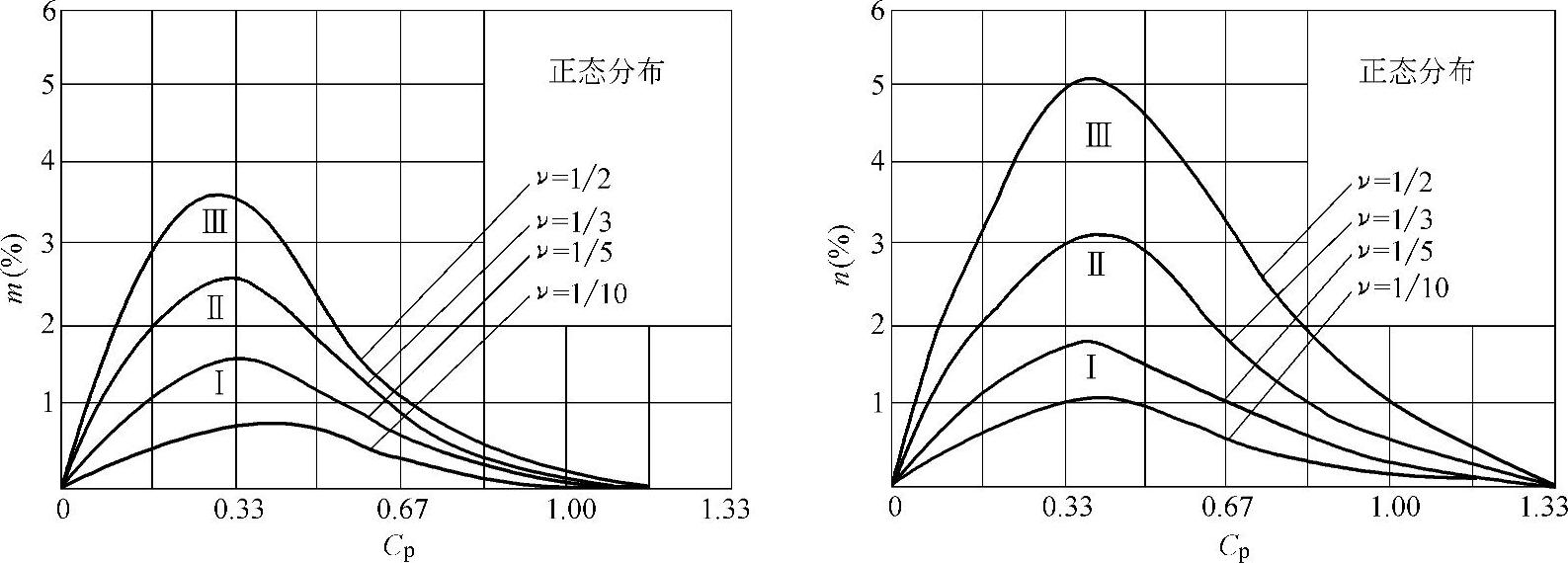
图1-37 正态分布时误收率m与误废率n

表1-24 正态分布时误收率m与误废率n

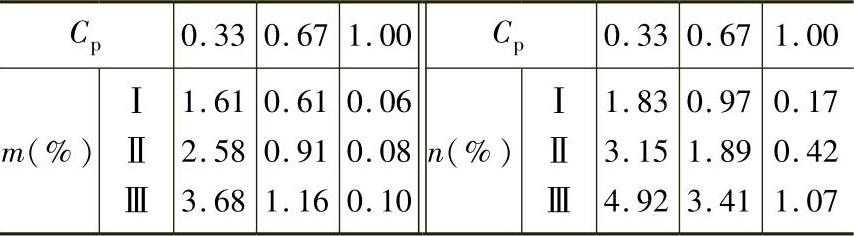
由图1-37或表1-24可见，工件尺寸与测量均遵循正态分布，通常m与n值都不大，例如：C_p=0.67，m约为1%，n约为2%；C_p=1，m约为0.08%，n约为0.4%。

工件尺寸遵循正态分布，而测量误差遵循均匀分布时，u=1.73s，这时m与n值均增加约10%。

2）工件尺寸遵循偏态分布：

偏态分布：在单件生产条件下，工件尺寸可能趋向偏态分布。现引用β分布描述偏态分布，其方程式为

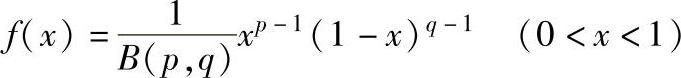
令p=1.5、q=3或反之p=3、q=1.5，得偏向不同的两种偏态分布，如图1-38所示。这时：

f（x）=6.5625x^0.5（1-x）²或

f（x）=6.5625x²（1-x）^1.5

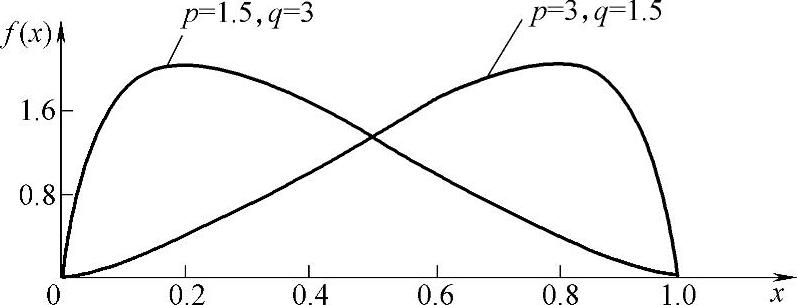
图1-38 偏态分布

该分布数学期望E（x）、标准差σ、相对不对称系数e、相对分布系数K分别为；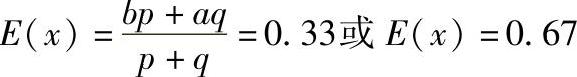

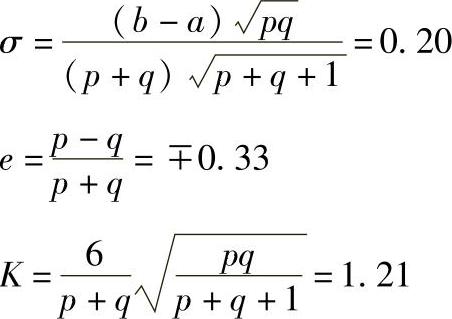
此处a=0，b=1，偏态分布及其参数如图1-39所示。

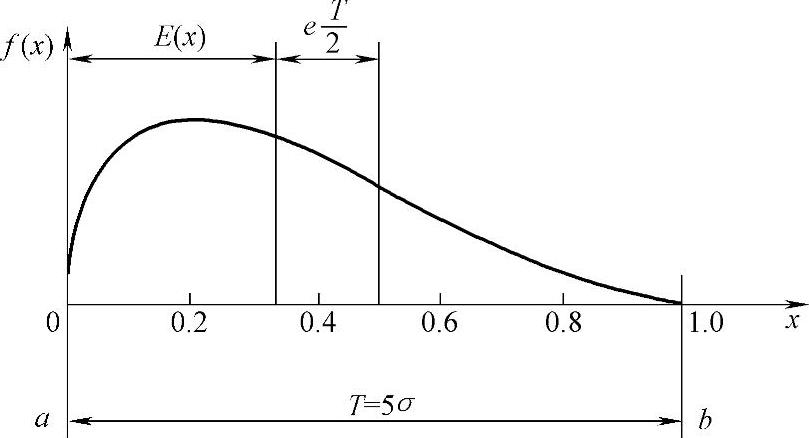
图1-39 偏态分布及其参数(www.xing528.com)

2）误判概率：验收极限按7.1.2节方式B决定，即A=0。工件尺寸遵循偏态分布，；测量误差遵循正态分布并取u=2s。这时m与n值见图1-40及表1-25。

表1-25 偏态分布时误收率m与误废率n

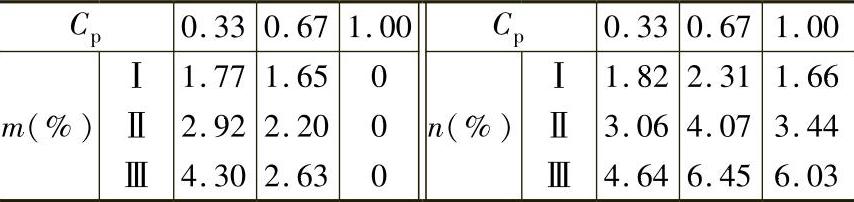
由图1-40或表1-25可见，工件尺寸遵循偏态分布时，m与n值均比正态分布时增加1倍多。例如：C_p=0.67，m约为2%，n约为4%；C_p=1，m=0，n约为3%。

工件尺寸遵循偏态分布，而测量误差遵循均匀分布时，u=1.73s，这时m与n值均增加约10%。

3）工件尺寸遵循均匀分布：验收极限按7.1.2节方式B决定，即A=0。工件尺寸遵循均匀分布，C_p=T/3.46σ；测量误差遵循正态分布并取u=2s。这时m与n值见图1-41及表1-26。

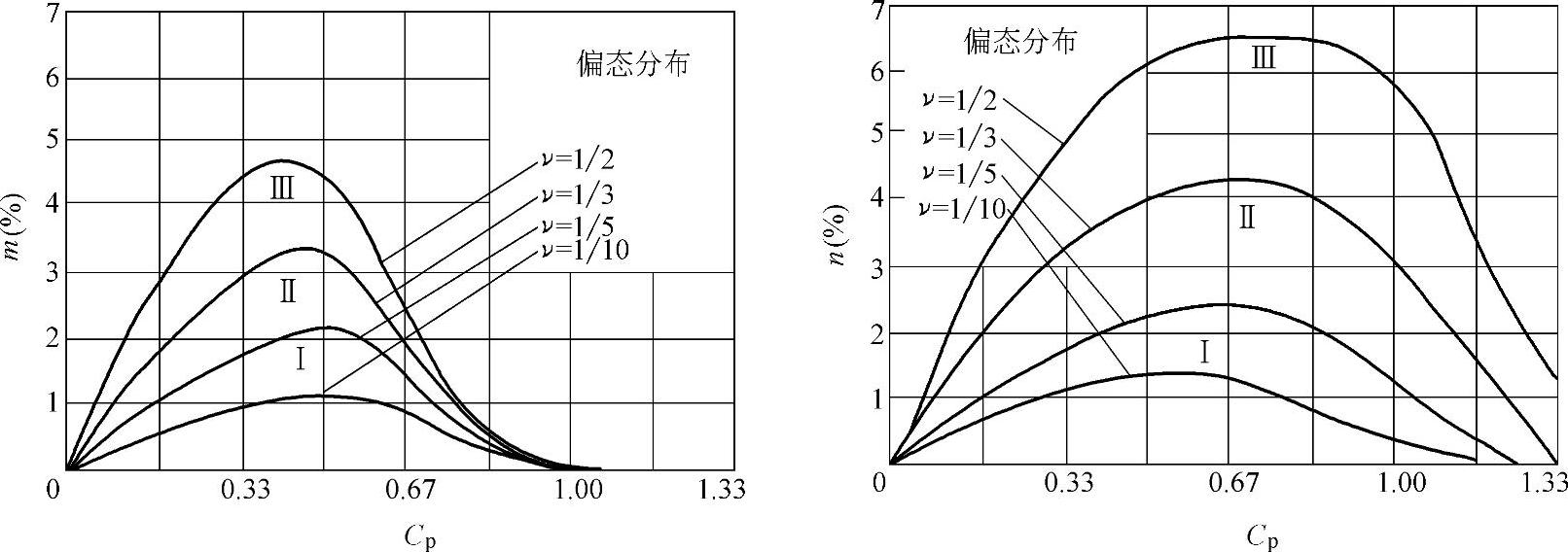
图1-40 偏态分布时误收率m与误废率n

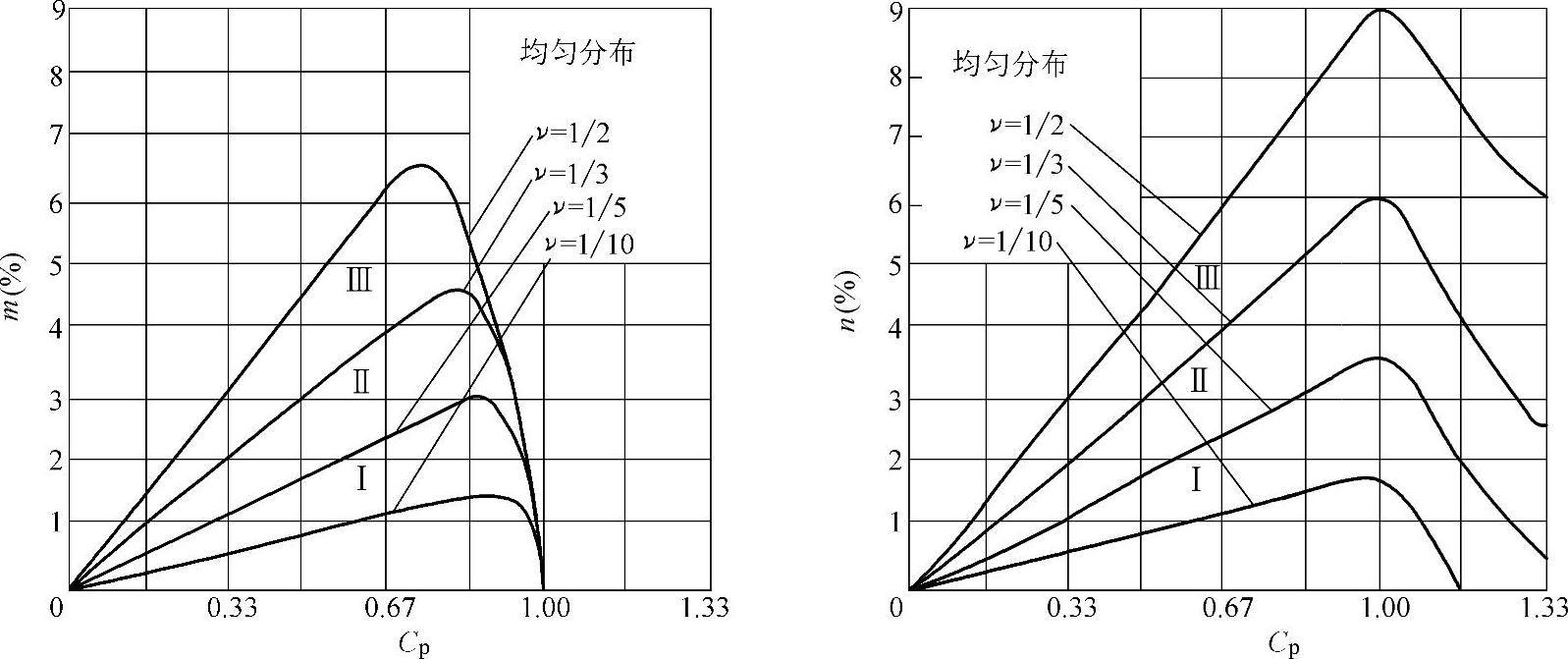
图1-41 均匀分布时误收率m与误废率n

表1-26 均匀分布时误收率m与误废率n

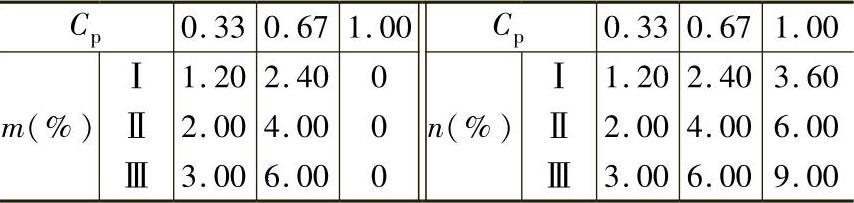
由图1-41或表1-26可见，工件尺寸遵循均匀分布时，m与n值均比正态分布时增加了1倍到2倍。例如：C_P=0.67，m与n值均为4%；C_p=1，m=0，n=6%。

工件尺寸遵循均匀分布，测量误差亦遵循均匀分布时，u=1.73s，这时m与n值均增加约30%。

（3）按方式A决定验收极限验收工件时的误判概率：令A=0、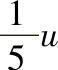、、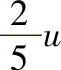、、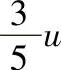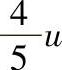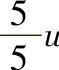，得不同的验收极限。取C_p=0.67时，工件尺寸在不同分布条件下，按不同验收极限验收工件时的误判概率。从图1-42～图1-44可见，随A值增大，m值迅速下降，n值急剧上升。

GB/T 3177—2009为使m值降到很小，n值又不致过大，采用多种验收极限：当C_p≥1时，Ⅰ、Ⅱ、Ⅲ各档均取A=0，即不内缩，以工件极限尺寸作为验收极限；当C_p＜1时，Ⅰ档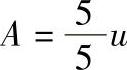，即100%内缩；Ⅱ档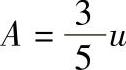，即60%内缩；Ⅲ档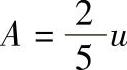，即40%内缩，按此决定各验收极限。

1）工件尺寸遵循正态分布：工件尺寸遵循正态分布时，不同验收极限得出的m与n值见图1-42及表1-27。由图1-42或表1-27可见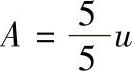，时，误收率m值为零，但误废率n值过大，甚至高达30%。按GB/T 3177—2009规定各验收极限的m与n值见表1-28。应当注意：配合尺寸只有当C_p≥1时，才允许用A=0。因此表1-28中m或n第1项数值，取自表1-24中C_p=1时的相应数值。

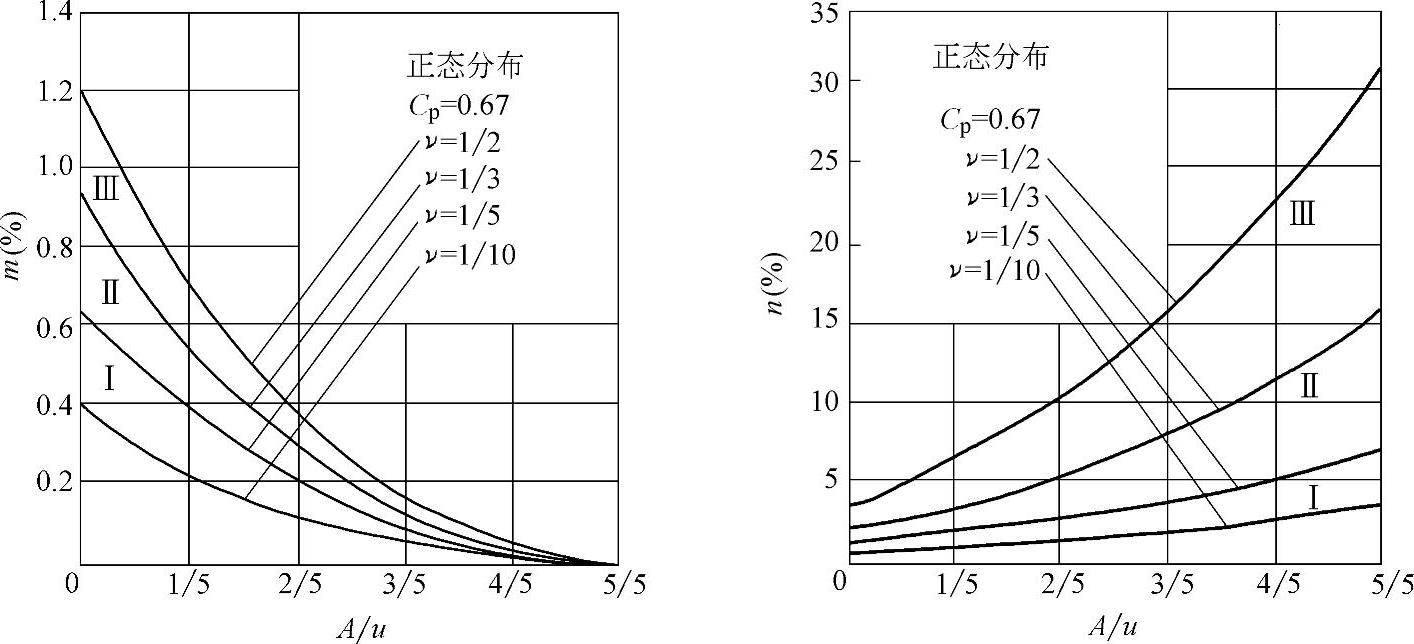
图1-42 正态分布时m、n值随A值的变化

表1-27 正态分布时m、n值随A值的变化

表1-28 正态分布时按GB/T 3177—2009规定各验收极限的m与n值

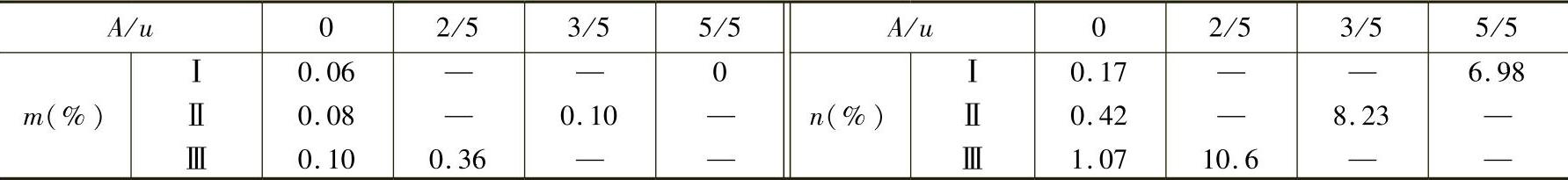
2）工件尺寸遵循偏态分布：工件尺寸遵循偏态分布时，不同验收极限得出的m与n值见图1-43及表1-29。由图1-43或表1-29可见，各m与n值均比正态分布时相应值大。按GB/T 3177—2009规定验收极限的m与n值见表1-30。表1-30中m或n的第1项数值取自表1-25中C_p=1时的相应数值。

表1-29 偏态分布时m、n值随A值的变化

表1-30 偏态分布时按GB/T 3177—2009规定各验收极限的m与n值

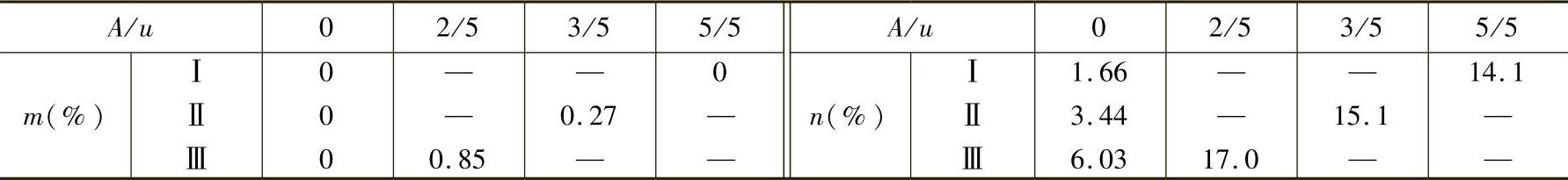
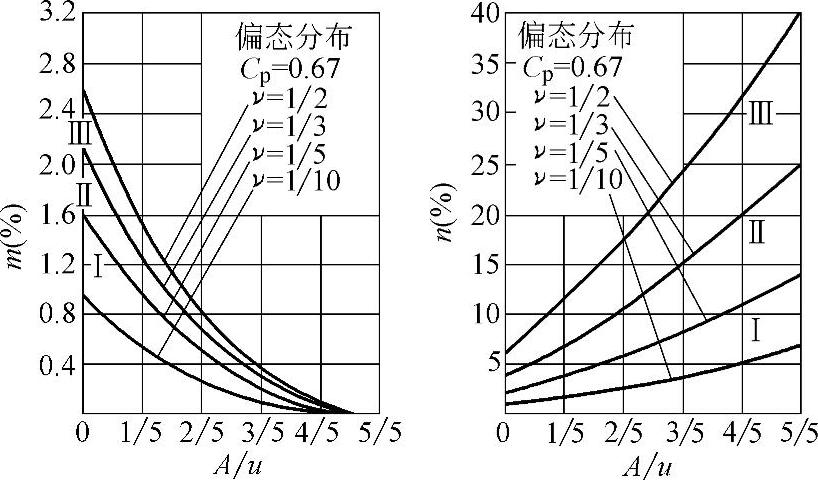
图1-43 偏态分布时m、n值随A值的变化

3）工件尺寸遵循均匀分布：工件尺寸遵循均匀分布时，不同验收极限得出m与n值见图1-44及表1-31。由图1-44或表1-31可见，各m与n值均比正态分布时相应值大，按GB/T 3177—2009规定验收极限的m与n值见表1-32。表1-32中的m或n的第1项数值，取自表1-26中C_p=1时的相应数值。

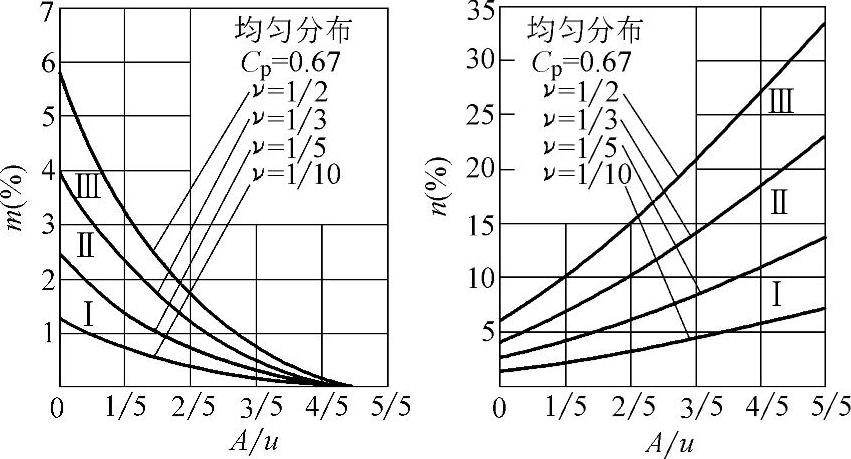
图1-44 均匀分布时m、n值随A值的变化

表1-31 均匀分布时m、n值随A值的变化（摘自GB/T 3177—2009）

表1-32 均匀分布时按GB/T 3177规定各验收极限的m与n值（摘自GB/T 3177—2009）

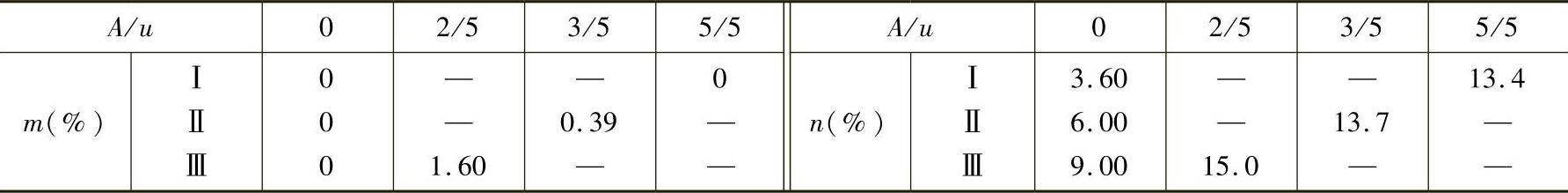
根据上述按方式B和方式A验收极限验收工件量的提高。时的误判概率的分析和计算可知，过程能力指数C_p当过程能力指数C_p大于等于1，工件尺寸近于的大小及工件尺寸的分布形式，是影响验收工件时正态分布时，误收率m接近于零，误废率n亦小，由测量误差引起的误判概率（误收率与误废率）的此时可按极限尺寸验收工件，不内缩。工件尺寸呈主要因素，测量误差的大小系非主要因素。因此，现偏态分布或均匀分布时，m为零，误废率n有一提高工件质量的基本措施应当是不断优化加工工艺定数量。过程，提高过程能力指数，尽量使工件尺寸趋近正当C_p小于1，误收率m和误废率n均较大，给态分布，是提高产品质量的保证；优化测量过程，予安全裕度时，可使m下降，但n上升。力求m控提高测量精度，有利于降低误判概率，促进产品质制在约千分之几，n控制在10%左右。