概率统计的基本原理与应用

（1）总体和样本

在一个具体的问题中，所考察对象的全体组成的集合称为总体。例如国家进行人口普查，那么总体就是全国人民；又如考察某一个航空公司的航班准点情况，那么每个航班的延误时间一起组成总体。很多时候考察总体比较麻烦或者没有必要，我们就从总体中抽出部分进行考察，那个抽出来的部分就称为样本，或者子样。考察航空公司的航班准点情况得到的数据永远是子样，除非这个航空公司关门了。

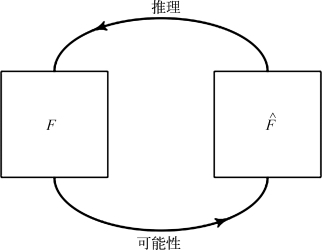
图2-30　推断与可能性互相影响

在统计分析中经常要根据样本来确定总体的情况，这个过程称为推理或者推断。我们用图2-30来解释可能性与推断的关系。左面的犉表示总体，右面的表示样本。从总体中选出一个样本是不确定事件，例如从一个有40人的班级中随机抽取5人去参加数学能力测试，那么犉就是这个班级的数学水平，而则是这5名学生的数学水平。要求从这5个人的测试结果去推断整个班级，这就是上方的弧线；显然抽取的人数越多推断就越可靠，在这个问题中抽取的人数就是下方的弧线，这里称为可能性。这里有两个问题，一个是推断的方法问题，怎样推理才算科学的？第二个是效率问题，怎样选取样本才能高效？这两个问题是本节讨论的对象。

（2）期望与方差

假如从A班选出的5名同学，他们测试成绩分别为97分，93分，80分，65分和50分；从B班选出的5名同学，他们测试成绩分别为92分，83分，78分，75分和60分。那么A班5名同学的平均成绩是（97＋93＋80＋65＋50）÷5＝77（分）。这个77分称为均值。一般，如果样本有n个元素，每个元素的值分别是x1，x2，…，xn，那么

就称为x1，x2，…，xn的均值，或者数学期望，简称期望值，期望也记成E（x）。类似地，可以求出B班5名同学成绩的均值是77.6。

顾名思义，均值代表的是平均水平，根据上面的计算，我们有理由认为B班的同学的数学成绩略高于A班，这个结论就是推断。显然每个班级选出的人数越多，那么根据均值比较得出哪个班级数学成绩好的推断就越有道理，这就是图2-29的意思。

思考：请结合A，B班的平均成绩谈你的具体想法？

我们用样本来推断总体时，需要考虑两个问题：科学性和效率。对此我们比较一下A班、B班的平均值和实际个案，发现两个样本的平均值仅相差0.6，但是实际样本情况却是完全不同的：B班5个同学的成绩最高分为92分，最低分为60分，相对集中在均值中；而A班5个同学成绩相差很大，最高分达97分，最低分却到50分，没有70左右的分数。这显然反映出A班B班截然不同的情况，而我们计算可知均值无法体现这种差异。那么是否存在一种方法能更好反映出这种特殊情况呢？

97-77表示了A班最好同学与平均成绩的差，这个值称为离差或者偏差。可以算出A班5位同学的偏差分别是20，16，3，-12，-27。为了消除正负号带来的影响，通常求取它们的平方后再求平均值，就是计算

DA称为A班5名同学成绩的方差。方差越大说明数据分布得越分散。用同样的方法可以求出B班5名同学成绩的方差，DB＝10.519，小于DA，这说明B班同学的水平比较均匀，这个事实也可以从得分情况直接看出。一般，如果选取的样本有n个元素，每个元素的值分别是x1，x2，…，xn，那么方差是

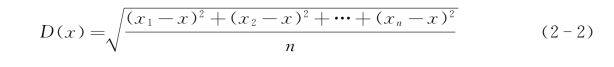
（3）随机变量及其分布

在上面的例子中，x1是A班抽出5个同学中数学测试的最好成绩。这个x1具有不确定性。首先从A班抽出哪5个同学是不确定的，其次即使5个同学选定了，谁的测试成绩最好也是不确定的，最后即使我们知道抽出的5个同学中张三的平时成绩最好，但这次测试得几分还是个未知数。这种取值不能确定的变量称为随机变量。完整地说：“从A班抽出5个同学进行数学测试，其中最好的成绩是一个随机变量。”类似地，E（x）和D（x）也都是随机变量。

设x是一个随机变量，x≤a就是一个随机事件，简称事件，例如上述的x1≤97就是一个随机事件，指A班抽出5个同学中数学测试的最好成绩不高于97分。类似地，x1＞90和90≤x1≤97都是随机事件，根据上面的叙述中读者不难明确这两个随机事件表达的意义。

x≤a是随机事件，我们用P（x≤a）表示这个随机事件发生的概率。继续前面的例子，如果取a＝-1，那么x1≤-1是不可能的，就称x1≤-1的概率是0，即P（x1≤-1）＝0；如果取a＝101，那么x1≤101是必然的，就称它的概率是1，记为P（x1≤101）＝1。这个例子表明P（x≤a）是a的函数，我们将这个函数记成F（a）＝P（x≤a），函数F（a）就称为是随机变量x的分布函数，简称分布。

为了与通常的记法一致，人们将x换成ξ，将a换成x，这样分布就可以表示为大家熟悉的形式F（x）了。分布是一个函数，那么就可以求导，已经证明分布函数是几乎处处可以求导的，记，这个f（x）称为随机变量ξ的密度函数。根据密度函数的定义，自然成立

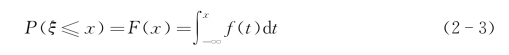
图2-31解释了式（2-3）的几何意义，图中的曲线就是密度函数，x是任意一个实数，图中的阴影部分面积就是P（ξ≤x）＝F（x）。

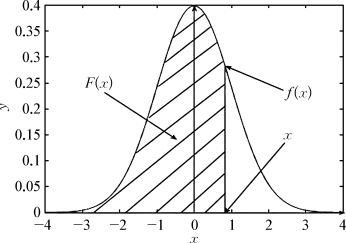
图2-31　密度函数与概率的关系

分布具有下列基本性质：(www.xing528.com)

F（x）≥0，对一切实数x成立；

如果x1≥x2，那么F（x1）≥F（x2）；

F（-∞）＝0，F（∞）＝1。

相应地，密度函数的性质是：

f（x）≥0，对一切实数x成立；

f（-∞）＝f（∞）＝0；

。

如果在n次试验中，随机事件ξ≤A出现m次，那么m／n称为ξ≤A出现的频率，概率论中的一个大数定律这样说：

大数定律　。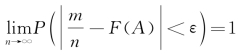

概率论中有多个大数定律，这个称为伯努利大数定律，它可以理解成只要试验的次数足够多，那么频率就会无限地逼近概率。

（4）正态分布

已知的分布有很多，像均匀分布、二项分布、泊松分布等，其中最常用的是正态分布（也称高斯分布），正态分布记成N（μ，σ2），其中μ是期望，σ是方差，σ是正数。随机变量ξ服从正态分布记成ξ～N（μ，σ2）。正态分布的密度函数f（x）如下：

f（x）的图象见图2-31。

图2-32给出均值相同方差不同的正态密度函数的图象。这个图象关于均值x＝μ对称，方差越小图形显得越尖，最大值也越大。正态分布的密度曲线也称高斯曲线或钟形曲线。

均值是0，方差是1的正态分布称为标准正态分布，记成N（0，1）。很多统计的书会附有标准正态分布表供大家查阅。对于ξ～N（μ，σ2），总可以通过变换

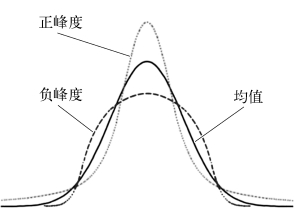
图2-32　正态分布密度函数的图象

转化成标准正态分布，即η～N（0，1）。

正态分布之所以重要是因为有下面的定理。

中心极限定理　如果ξ1，ξ2，…，ξn相互独立，并且都服从均值为μ，方差为σ的（任意一个）分布，那么当n充分大的时候，ξ1＋ξ2＋…＋ξn近似地服从N（nμ，nσ2）。

3σ准则　正态分布的另一个重要性质是所谓的3σ准则（图2-33）。对于任意一个正态分布，图2-33中-1σ～1σ部分面积就是F（μ-σ≤x≤μ＋σ）＝2×34.1%＝68.2%，就是说对于一个正态分布来说，任意抽样得值a，那么这个a有68.2%的可能落在区间（μ-σ，μ＋σ）中，有99.7%的可能落在（μ-3σ，μ＋3σ）中。因此近似地讲一个正态分布的值基本在（μ-3σ，μ＋3σ）中，这个事实称为3σ准则。

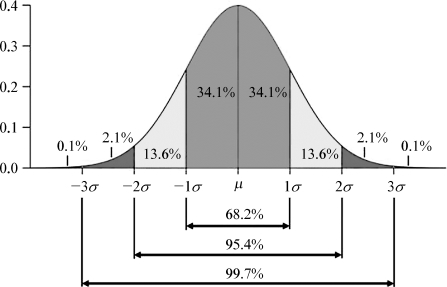
图2-33　3σ　准则