【摘要】：例如，对数转换，数据点y意味着我们定义新的数据点zz＝log我们想要进行转换的一个常见的例子就是数据全部都呈正，但接近零值。图2-25原始数据VS转换数据成图对比代码图2-26原始数据VS转换数据成图原始数据转换数据那么这样做会不会弄乱我们的数据呢？图2-27数据转换后飞机航班数据箱形图代码图2-28回顾成对比较图2-29转换后数据图
当数据呈现偏态分布的时候[8]，可能很难比较，因为有许多数据在一端聚拢，但当轴覆盖了值比较大的数据，而这些数据的比例相对较小时，我们的注意力也就常被比较大的值吸引。
解决这个问题的一个常见方法是转换该数据，这只是意味着我们选择一个函数来转换数据，而并非改变数据本身。例如，对数转换，数据点y意味着我们定义新的数据点z
z＝log（y）
我们想要进行转换的一个常见的例子就是数据全部都呈正，但接近零值。在这种情况下，如果是通常有很多数据都集中在零（因为该数据不能变得更小了），如果我们使用了log转换之后就会变得更加易于分析（图2-23，图2-24）。
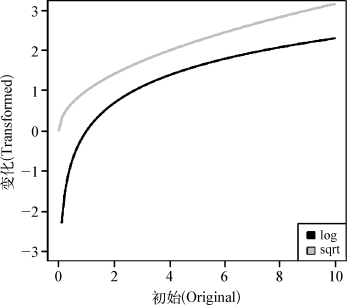
图2-24 转换数据函数图形展示
你可以看到原来被4分开的（6，10）的两个“数据”值，现在在变换后的比例上大约是1／2个单位，而两个“数据”曾经被4分隔的值（2，6）现在被1分开。而这个“拉伸”的数据在右边要分得更开一些，而左边则更近一些。在接下来的例子当中，我将会创造一些“假”的数据，使这个概念更加易于理解（图2-25，图2-26）。
图2-25 原始数据VS转换数据成图对比代码(www.xing528.com)
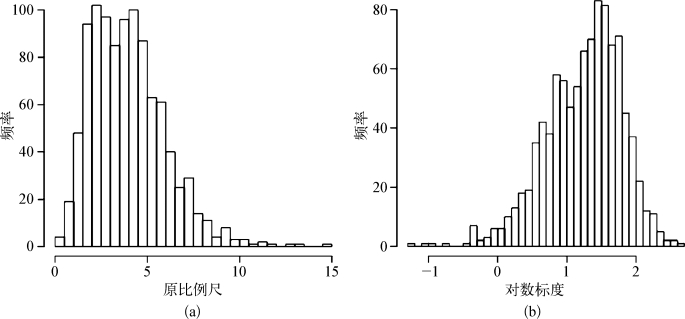
图2-26 原始数据VS转换数据成图
（a）原始数据 （b）转换数据
那么这样做会不会弄乱我们的数据呢？
需要注意一个重要的属性是这些“单一方程”，意味着所保留的是数据的排名，而并不是把原有数据的顺序也打乱了。也就是当你移动到对数刻度，请测试以下代码（图2-27）。
图2-27 数据转换后飞机航班数据箱形图代码
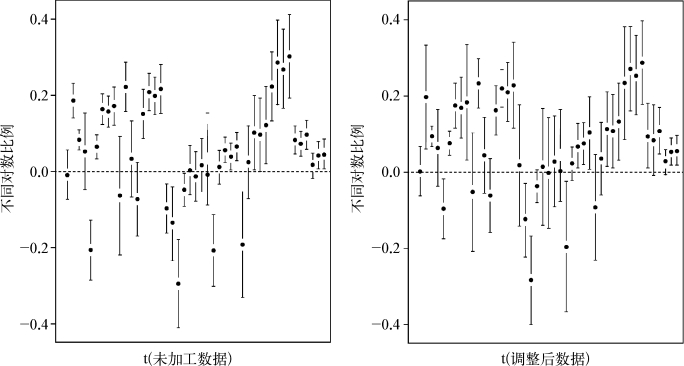
图2-28 回顾成对比较
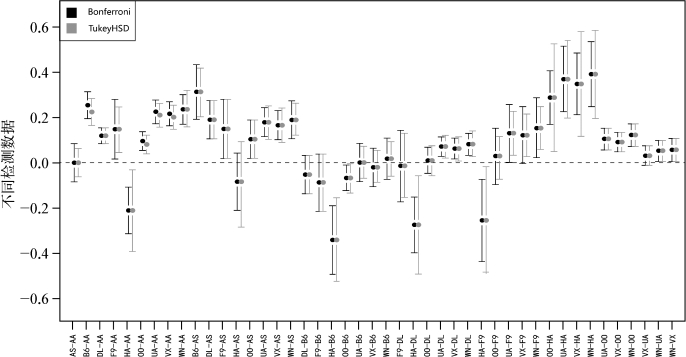
图2-29 转换后数据图
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
