在使用仪表测量工艺参数时,不仅需要知道仪表的指示值,还需要了解测量值的误差范围。由于所选用的仪表准确度的限制、实验手段的不完善、环境中各种干扰的存在以及检测技术水平有限,在检测过程中仪表测量值与真实值之间总会存在一定的差值。这个差值就是误差。
1.误差的种类
根据误差的性质不同,可分为三个大类。
(1)系统误差
在相同的条件下,对同一物理量进行多次测量,如果误差按照一定规律出现,则把这种误差称为系统误差,简称系差。系统误差可分为定值系统误差(简称定值系差)和变值系统误差(简称变值系差)。数值和符号都保持不变的系统误差称为定值系差。数值和符号均按照一定规律性变化的系统误差称为变值系差。变值系差按其变化规律又可分为线性系统误差、周期性系统误差和按复杂规律变化的系统误差。如图2-6所示,其中1为定值系统误差,2为线性系统误差,3为周期系统误差,4为按复杂规律变化的系统误差。

图2-6 系统误差示意图
系统误差的来源包括仪表制造、安装或使用方法不正确,测量设备的基本误差、读数方法不正确以及环境误差等。系统误差是一种有规律的误差,可以通过理论分析采用修正值或补偿校正等方法来减小或消除。
(2)随机误差
当对某一物理量进行多次重复测量时,若误差出现的大小和符号均以不可预知的方式变化,则该误差为随机误差。随机误差产生的原因比较复杂,虽然测量是在相同条件下进行的,但测量环境中温度、湿度、压力、振动、电场等总会发生微小变化。因此,随机误差是大量对测量值影响微小且又互不相关的因素所引起的综合结果。随机误差就个体而言并无规律可循,但其总体却服从统计规律,总的来说随机误差具有以下特性:
1)对称性:绝对值相等、符号相反的误差在多次重复测量中出现的可能性相等。
2)有界性:在一定测量条件下,随机误差的绝对值不会超出某一限度。
3)单峰性:绝对值小的随机误差比绝对值大的随机误差在多次重复测量中出现的机会多。
4)抵偿性:随机误差的算术平均值随测量次数的增加而趋于零。
随机误差的变化通常难以预测,因此也无法通过实验方法确定、修正和清除。但是通过多次测量比较可以发现随机误差服从某种统计规律(如正态分布、均匀分布、泊松分布等)。
(3)粗大误差
粗大误差指由于仪表产生故障、操作者疏忽大意或重大外界干扰而引起的显著偏离实际值的误差。这种误差对测量结果影响很大,应该尽量避免出现。多次测量中出现的粗大误差,应作为异常值去除。
2.误差处理
(1)减小系统误差的方法。
1)消除系统误差产生的根源。
为减小系统误差的影响,应该从测试系统的设计时入手。选用合适的测量方法以避免方法误差;选择最佳的测量仪表与合理的装配工艺,以减小工具误差;选择合适的测量环境以减小环境误差。此外,还需定期检查、维修和校正测量仪器以保证测量的准确度。
2)引入更正值法。
该方法主要用于消除定值系统误差。在测量之前,通过对测量仪表进行校准,可以得到更正值,将更正值加入测量值中,即得到被测量的真值。应该注意的是,更正值本身的误差应小于所要求的测量误差。由于更正值本身也存在误差,因此系统误差并没有完全消除,只是被大大地削弱了。
更正值一般用C表示,它是与测量误差的绝对值相等而符号相反的值。更正值给出的方式不一定是具体的数值,也可以是一条曲线、公式或数表。在某些自动检测系统中,预先将更正值储存于计算机的内存中,这样可对测量结果中的系统误差自动进行修正。
3)采用特殊测量方法消除系统误差。
①直接比较法。直接比较法即零位式测量法,用于消除定值系统误差。该方法的优点在于当指示器的灵敏度足够高时,测量的准确度取决于标准的已知量,而标准量具的误差是很小的。
②替代法。替代法主要用于消除定值系统误差。其操作方法为用可调的标准量具取代被测量x接入测量仪表,通过调节标准量具A的值使测量仪表的示值与被测量接入时相同,于是有x=A。
例如,测量某未知电阻Rx,要求误差小于0.1%。首先将它接入一个电桥中(见图2-7),该电桥的误差为1%。调整桥臂电阻R1、R2使电桥平衡;然后取下Rx,换上标准电阻箱Rs(电阻箱为0.01级)。保持R1、R2不动,调节Rs的大小,使电桥再次平衡,此时被测电阻Rx=Rs。只要测量灵敏度足够,根据这种方法测量的Rx的准确度与标准电阻箱的准确度相当,而与检流计和电阻R1、R2的恒值误差无关,因此可以满足测量要求。

图2-7 替代法测电阻
替代法的特点是被测量与标准量具通过测量装置进行比较,测量装置的系统误差不带给测量结果,它只起辨别有无差异的作用。因此测量装置的灵敏度应该足够高,否则不能得到期望的结果。
③交换法。这种方法是指当测量仪表内部存在固定方向的误差因素时,将测量中的某些条件(如被测物的位置或被测量的极性等)相互交换,使产生系差的原因对先后两次测量结果起反作用,将这两次测量结果加以适当的数学处理(通常取其算术平均值或几何平均值),即可消除系统误差。
例如,用等臂天平测量质量时,由于天平左右两臂长的微小差别,会引起测量的定值系统误差。如果将被称物与砝码在天平左右两盘上分别各称量一次,取两次测量平均值作为被称物的质量,这时测量结果中就不含有因天平不等臂引起的系统误差。
④微差法。这种方法是将被测量与已知的标准量进行比较,取其差值,然后用测量仪表测量这个差值。微差法只要求标准量与被测量相近,而用指示仪表测量其差值。这样,指示仪表的误差对测量的影响会大大减弱。

图2-8 线性系统误差
⑤等时距对称观测法。等时距对称观测法用于消除线性系统误差。由于线性系统误差按照图2-8所示的斜线规律变化,其特点为对称于中点t3的各系统误差的算术平均值彼此相等,即

利用上述关系,将测量对称安排,取两次对称测量值的平均值作为测量结果即消除系统误差。由于多数变值系统误差在短时间内均可认为是按线性规律变化的,即使按复杂规律变化的误差,其一次近似亦为线性误差。因此,在许多精密测量场合,均可采用等时距对称观测法消除变值系差。
⑥半周期观测法。半周期观测法用于消除周期性的系统误差。设周期性系统误差的变化规律为

式中,θ为决定周期性误差的自变量;T为周期性系统误差的变化周期。
在某一时刻,如θ=θ0,周期性误差为

经过半个周期后, ,周期性误差为
,周期性误差为

可见,如果在某处测得一个数据后,在与该点相隔半个周期处再测量一个数据,取两次测量的平均值作为测量结果,即可消除周期性系统误差。
(2)随机误差的估算
1)标准差。
标准差σ定义为

式中,xi为每次测量的测量值;x0为被测量的真值。
σ是一定测量条件下随机误差最常用的估计值。其物理意义为随机误差落在(-σ,+σ)区间的概率为68.3%,区间(-σ,+σ)称为置信区间,相应的概率称为置信概率。显然,置信区间扩大,则置信概率提高。置信区间取(-2σ,+2σ)时,置信概率为95.4%;置信区间取(-3σ,+3σ)时,置信概率为99.7%。
定义3σ为极限误差,其概率含义是在1000次测量中只有3次测量的误差绝对值会超过3σ。由于在一般测量中次数很少超过几十次,因此,可以认为测量误差超出±3σ范围的概率是很小的,故称为极限误差,一般可作为可疑值取舍的判定标准。
由上面分析知,在一定的置信概率下,真值m一定落在以测得值x0为中心,以误差限±kσ(k为置信系数)为区间的一个范围内,即m=x±kσ。
比如,置信系数k=3,则置信概率为99.7%,故可以认为真值落在±3σ范围内的可信程度为99.7%。
2)单次测量值的标准差的估计。
由于真值未知时,随机误差Δxi不可求,可用各次测量值与算术平均值之差——剩余误差 来代替误差Δxi来估算有限次测量中的标准差,得到的结果就是单次测量的标准差,用
来代替误差Δxi来估算有限次测量中的标准差,得到的结果就是单次测量的标准差,用 表示,它只是一个估算值,有误差理论可以证明单次测量的标准差的计算式为
表示,它只是一个估算值,有误差理论可以证明单次测量的标准差的计算式为

这一公式称为贝塞尔公式。
同理,按ν2i计算的极限误差为 ,
,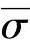 的物理意义与σ的相同。当n→∞,有n-1→n,则
的物理意义与σ的相同。当n→∞,有n-1→n,则 。在一般情况下,对于
。在一般情况下,对于 和σ的符号并不加以严格的区分,但是n较小时,必须采用贝塞尔公式计算σ的值。(https://www.xing528.com)
和σ的符号并不加以严格的区分,但是n较小时,必须采用贝塞尔公式计算σ的值。(https://www.xing528.com)
3)算术平均值的标准差的估计。
在测量中用算术平均值作为最可信赖值,它比单次测量得到的结果可靠性高。由于测量次数有限,因此 也不等于x0。也就是说,
也不等于x0。也就是说, 还是存在随机误差的,可以证明,算术平均值的标准差
还是存在随机误差的,可以证明,算术平均值的标准差 是单次测量值的标准差
是单次测量值的标准差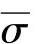 的
的 倍,即
倍,即
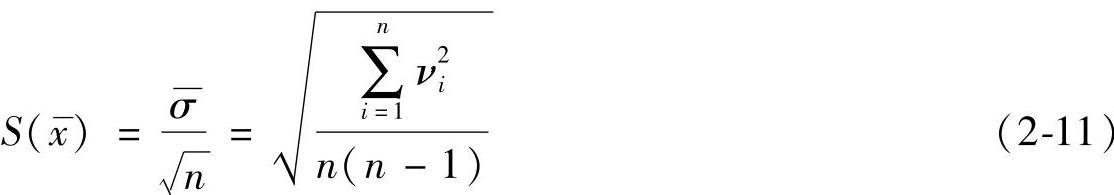
式(2-11)表明,在n较小时,增加测量次数n,可明显减小测量结果的标准差,提高测量的准确度。但随着n的增大,减小的程度越来越小;当n大到一定数值时 就几乎不变了。
就几乎不变了。
(3)粗大误差的判别和剔除
由于随机误差具有有界性,因此,测量结果明显不同于期望值的测量值含粗大误差(疏失误差),应该予以剔除。判别粗大误差的准则很多,下面介绍两种。
1)拉依达准则(3σ准则)。
当测量结果中仅含有随机误差,其测量数据呈正态分布时,误差的绝对值大于3σ的概率仅为0.00270,为小概率事件。由概率统计理论可知,小概率事件不易发生,因此,当测量次数为有限次时,若有剩余误差为
|νi|>3σ (2-12)
即可判定该测量数据含有粗大误差,应予以剔除。该准则简单、实用,但不适合于测量次数不大于10的情况,因为当n≤10时,剩余误差总是小于3σ。
2)格罗布斯准则。
当测量数据中,某数据xi的剩余误差满足
|νi|>g(a,n)σ (2-13)
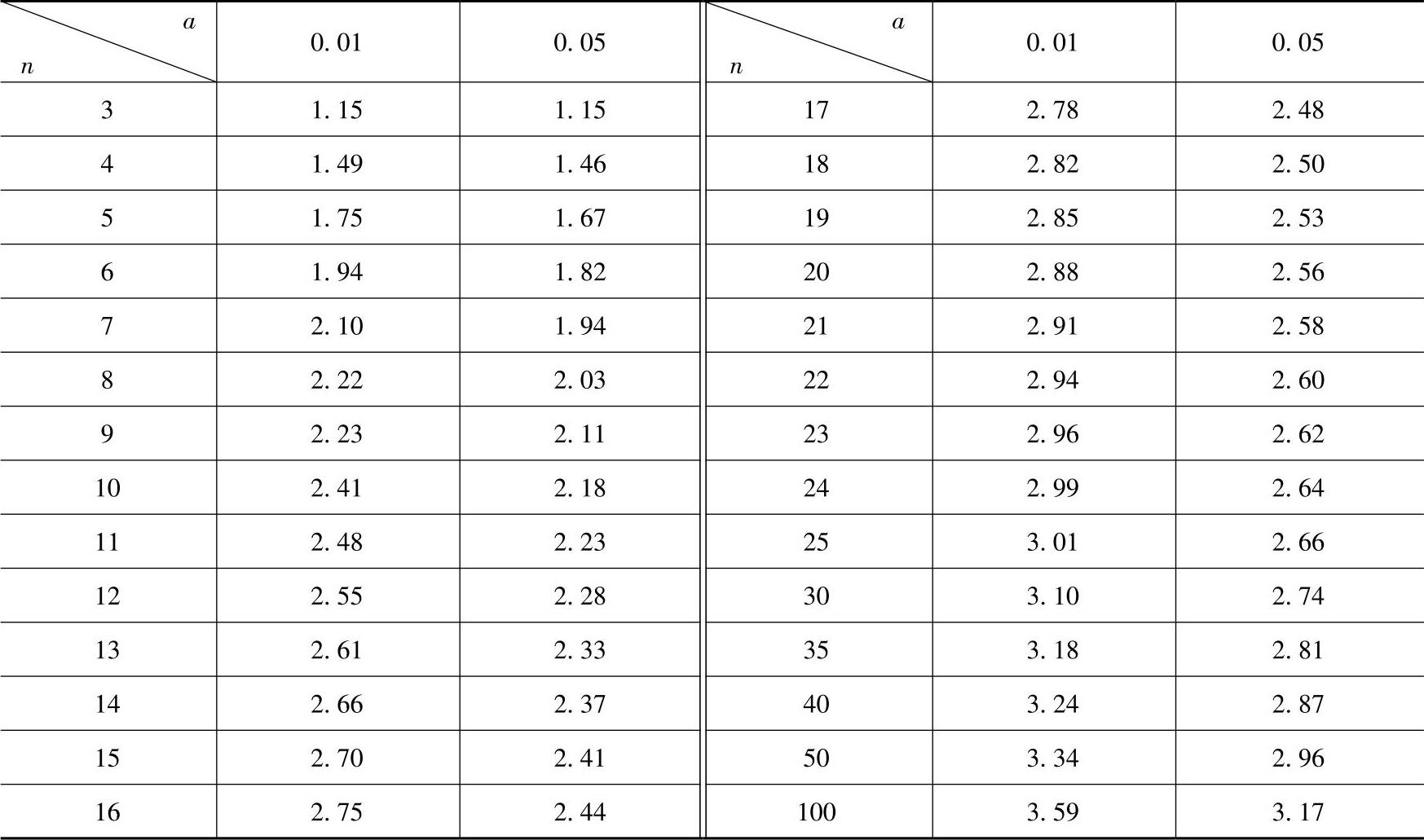
则该数据含有粗大误差,应予以剔除。式中,g(a,n)σ为格罗布斯准则鉴别值,g(a,n)为格罗布斯准则鉴别系数,它与测量次数n和显著性水平a有关,见表2-3,显著性水平a一般取0.01或0.05,置信概率p=1-a。
表2-3 格罗布斯准则鉴别值g(a,n)数值表
【例2-1】 对某被测量进行了15次重复测量,测量的数据为:10.01、10.02、9.98、10.03、10.02、9.97、9.99、10.01、10.03、10.27、9.97、10.02、9.99、10.01、9.98。试用拉依达准则和格罗布斯准则判定测量数据中是否存在粗大误差。解:将各测量值x,剩余误差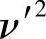 及ν2计算出来后填于表2-4中。
及ν2计算出来后填于表2-4中。
(1)用拉依达准则判断
因为3σ′=3×0.021=0.063,所以3σ=3×0.0722=0.2166由于第10个数据的剩余误差为0.25>3σ,说明该数据含有粗大误差应剔除。在剔除了第10个数据后重新计算 =10.002,并计算新的剩余误差ν′和ν′2填于表中。
=10.002,并计算新的剩余误差ν′和ν′2填于表中。
计算

由表2-4数据可知,所有14个测量数据的剩余误差的绝对值均小于0.063,所以不存在含有粗大误差的数据。
表2-4 测量结果计算表

3.误差的表示形式
测量误差按其表示方式可分为绝对误差和相对误差。
(1)绝对误差
绝对误差指测量值与被测量真值之间的差值,即
Δx=x-A (2-14)
式中,Δx为绝对误差;x为测量值;A为被测量真值。
在实际应用中,被测量的真值是无法得到的。因此,在一台仪表的量程范围内,各点读数的绝对误差是指用标准仪表(准确度较高)和该表对同一被测量测量时得到的两个读数的差值。即将式(2-14)中的被测量真值用标准仪表的读数来替代。
绝对误差不能确切地反映测量结果的准确程度,为此在实际测量中引入了相对误差,而绝对误差一般只适用于标准器具的标准,但它是相对误差表述的基础。
(2)相对误差
相对误差是仪表的绝对误差Δx与被测量真实值A之比,用百分比表示。但被测量的真值是无法得到的。通常有三种表示方法,即实际相对误差、示值相对误差和引用相对误差(又称满度相对误差)。
1)实际相对误差。实际相对误差γA是用绝对误差Δx与被测量的实际值A0的百分比值来表示的相对误差,即

2)示值相对误差。示值相对误差γx是用绝对误差Δx与被测量的示值(即测量值)x的百分比值表示的相对误差,即

实际相对误差和示值相对误差都是用来衡量测量值准确程度的。
3)引用(满度)相对误差。引用相对误差是用绝对误差Δx与仪表量程范围(Amax-Amin)的百分比值表示的相对误差,即

引用误差可用于判断仪表的质量,因为两只仪表如果绝对误差相同,但仪表量程不同时,显然量程范围大的那只仪表准确度更高些。
在采用引用误差来判断仪表质量时,我们会发现,对于同一个仪表,其量程范围固定,但是测量不同的点时,每个点的绝对误差会有所不同,这样我们就无法具体判定仪表的质量好坏。因此,人们引入了最大引用(满度)相对误差。它是用量程中最大绝对误差Δxmax与仪表量程范围(Amax-Amin)的百分比值表示,即

4.仪表的允许误差及准确度等级
根据仪表的使用要求,在正常使用条件下允许仪表具有的误差最大值,称为允许误差。允许误差一般用相对百分误差来表示,即一台仪表的允许误差是指在规定的正常情况下允许的相对百分误差的最大值。实际上,允许误差等同于最大引用(满度)相对误差,其表示形式为

式中,γ允max为仪表的允许误差;Δxmax为仪表允许的最大绝对误差;Amax-Amin为仪表的量程。
仪表的准确度等级又称精度等级或精度,是表示仪表测量结果可靠程度最重要的指标。仪表准确度可分为若干等级,其等级可用去掉允许误差中的正负号及百分符号后的数值确定。例如某台压力仪表的允许误差为2.5%,则认为该仪表的准确度等级为2.5级。
根据自动化仪表行业的规定,仪表准确度等级可分为:0.001级、0.005级、0.02级、0.05级、0.1级、0.2级、0.4级、0.5级、1.0级、1.5级、2.5级、4.0级、5.0级等。等级数越小,准确度越高。另外,我国模拟仪表有下列7种等级:0.1级、0.2级、0.5级、1.0级、1.5级、2.5级、5.0级。
通常,科学实验室用的仪表准确度等级小于0.05;工业检测用仪表的等级数多为0.1~2.5,其中校验用的多为0.1或0.2;现场用仪表多为0.5~2.5;我国生产的DDZ-Ⅲ型仪表的准确度等级为0.5级。
【例2-2】 某台压力仪表的测温范围为0~500kPa,校验该表得到的最大绝对误差为±3kPa,试确定该仪表的准确度等级。
解:该仪表的允许误差为

如果将仪表的允许误差去掉正负号和百分符号,其数值为0.6。由于仪表规定的准确度等级中没有0.6级仪表,同时,该仪表的允许误差超过了0.5级(±0.5%)。所以该压力仪表的准确度等级为1.0级。
【例2-3】 某台测温仪表的测温范围为100~1100℃,根据工艺要求,温度指示值的最大绝对误差不得超过±7℃。试问怎样选择仪表的准确度等级才能满足以上要求?
解:根据工艺要求,仪表的允许误差
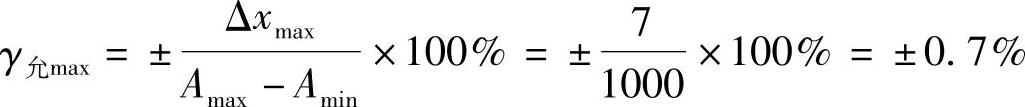
如果将仪表的允许误差去掉正负号及百分符号,其数值为0.7。此数值介于0.5~1.0之间。如果选择准确度等级为1.0级的仪表,其允许误差为±1.0%,超过了工艺上允许的数值,故应选择0.5级仪表才能满足工艺要求。
由以上两个例题可以看出,根据仪表的校验数据来确定仪表准确度等级和根据工艺要求来选择仪表的准确度等级,情况是不一样的。根据仪表的校验数据来确定仪表的准确度等级,仪表的允许误差应该大于(至少等于)仪表校验所得的最大相对百分误差;根据工艺要求来选择仪表准确度等级时,仪表的允许误差应小于(至多等于)工艺上所允许的最大相对百分误差。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




