转子侧变流器的矢量控制优化方案

转子侧变流器的控制目的是通过改变励磁电流的幅值和频率，实现变速恒频系统有功功率和无功功率的调节。

变速恒频风电机组的一个主要特点是发电机转速跟随风速的变化而变化，要保证并网侧的恒频恒压输出，必须从发电机的结构形式、电磁关系入手，制定控制策略。适用于绕线转子双馈式变速恒频风力发电机组的控制策略有矢量控制（FOC）、直接转矩控制（DTC）、直接功率控制（DPC）等。

由于双馈发电机的电路存在着磁路上的耦合，双馈发电机在三相坐标下的数学模型是非线性、时变的高阶系统，为了实现励磁电流和转矩电流（即有功功率和无功功率）的解耦控制，双馈发电机一般都采用矢量控制技术。

矢量控制的基本思想是，利用坐标变换将三相系统转换为二相系统，再通过按转子磁场定向的同步旋转变换实现了定子磁链分量与转矩电流分量的解耦，从而达到对交流电机的磁链与电流分别控制的目的。这样一来，交流电机可以等效为直流电机，控制转矩电流，获得与直流电机同样优良的静动态性能。

首先，讨论双馈发电机空间矢量模型。与前文相量模型一样，将转子侧参数都折算到定子侧（为了书写方便，这里不再加“’”），折算后的每相匝数都相等。

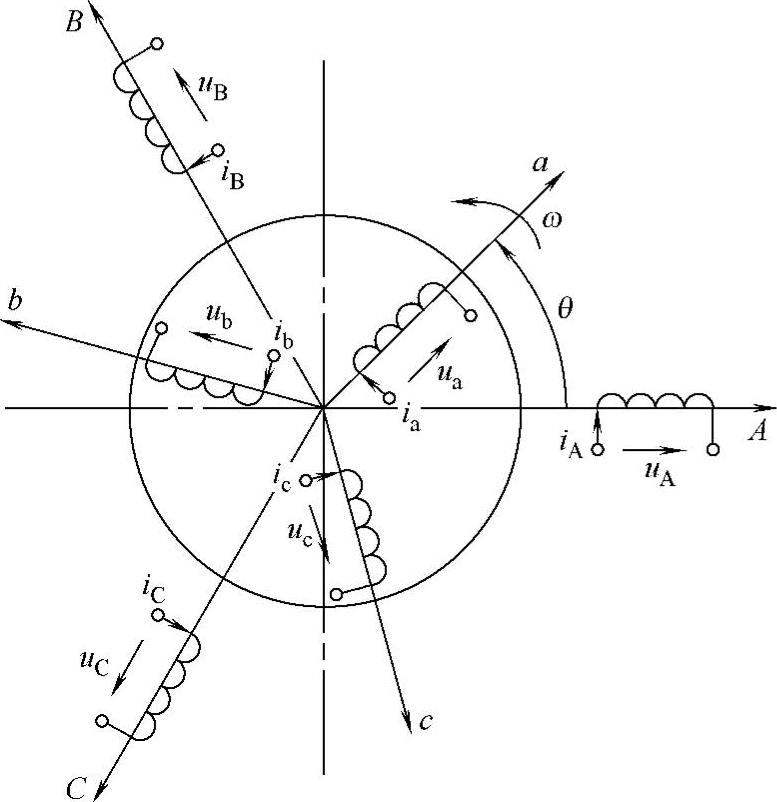
图8-25 三相异步电动机的物理模型

1.三相静止坐标系下电机模型

沿用本章第一节进行相量分析中的一些基本假设，并设定子三相绕组A、B、C在空间是固定的，以A轴为参考坐标轴，转子绕组轴线a、b、c随转子旋转，转子a轴和定子A轴间的电角度θ为空间角位移变量，规定各绕组电压、电流磁链的正方向符合电动机惯例。将双馈发电机等效为图8-25所示的三相异步电动机的物理模型。

经推导，三相静止坐标系下电机电压方程、磁链方程、运行方程和转矩方程如下：

（1）定子三相绕组（ABC）和转子三相绕组（abc）的电压方程

式中 u_A、u_B、u_C、u_a、u_b、u_c——定子三相绕组（ABC）和转子三相绕组（abc）的电压分量；

R₁、R₂——定、转子电阻；

i_A、i_B、i_C、i_a、i_b、i_c——定子三相绕组（ABC）和转子三相绕组（abc）的电流分量；

ψ_A、ψ_B、ψ_C、ψ_a、ψ_b、ψ_c——定子三相绕组（ABC）和转子三相绕组（abc）的全磁链；

p——微分算子d／dt。

（2）定、转子绕组的磁链方程

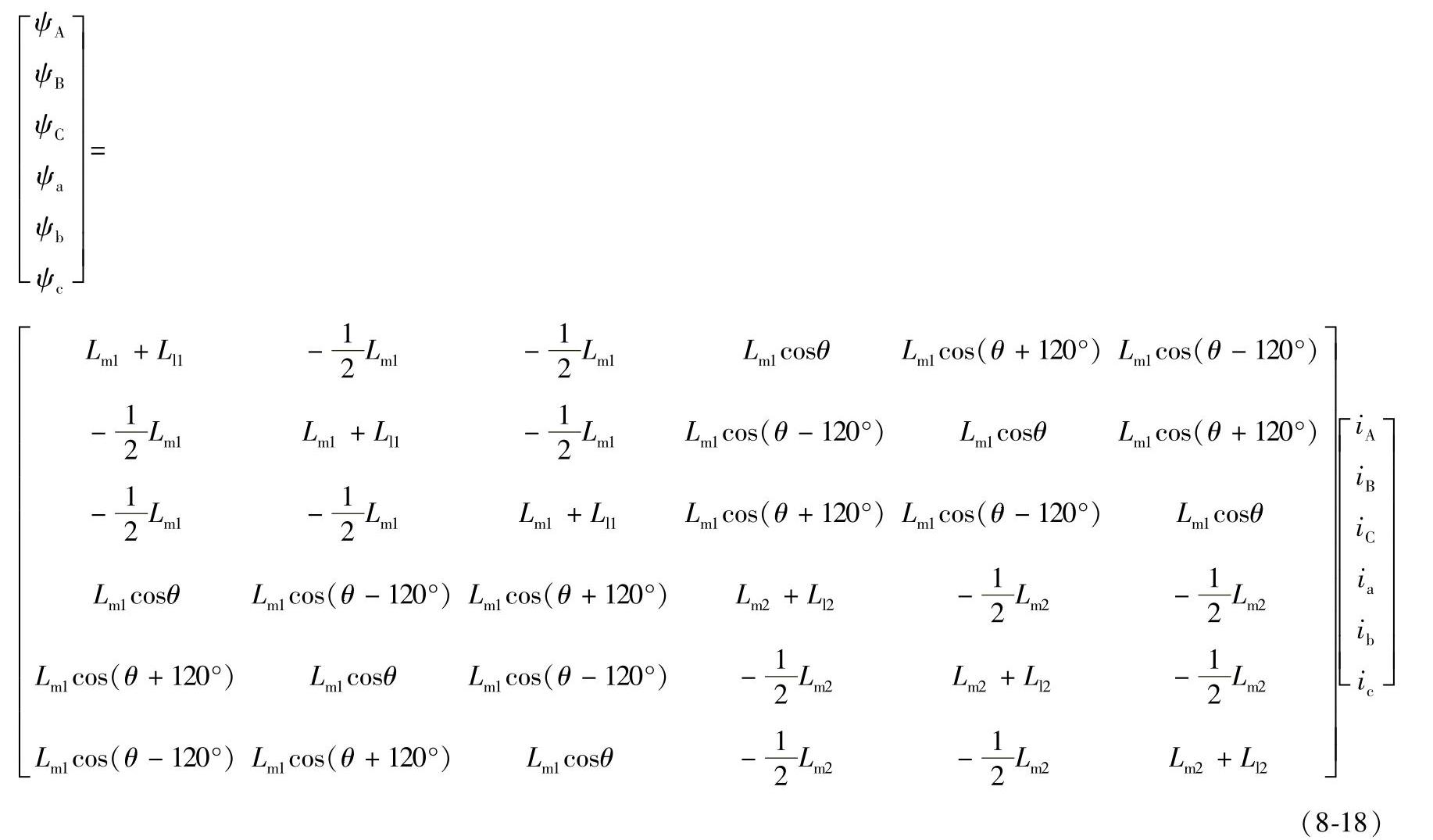
式中 L_m1——与主磁通对应的与定子一相绕组交链的最大互感磁通所对应的定子互感值；

L_m2——与主磁通对应的与转子一相绕组交链的最大互感磁通所对应的转子互感值，折算后有L_m1＝L_m2；

L_l1、L_l2——分别为定子漏感和转子漏感；

（3）转矩方程。电磁转矩的表达式为

M_e＝－pL_m1［（i_Ai_a＋i_Bi_b＋i_Ci_c）sinθ＋（i_Ai_b＋i_Bi_c＋i_Ci_a）sin（θ＋120°）＋（i_Ai_c＋i_Bi_a＋i_Ci_b）sin（θ－120°）］ （8-19）

（4）运动方程。应用电动机惯例，规定旋转方向为转矩的正方向，电机的运动方程是

式中 M_L——负载阻转矩，发电状态代之以驱动力矩M_m，单位为N·m；

M_e——电磁转矩，单位为N·m；

J——电机转子转动惯量，单位为kg·m²；

D——阻尼系数，单位为N·m·s；

p——电机极对数；

ω——转子电角速度，单位为rad／s，且有

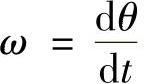
式（8-17）～式（8-20）是三相异步电机在相静止坐标下的数学模型。由于它具有非线性、时变、强耦合的特点，分析和求解困难。为了简化分析和应用矢量变换控制，可以通过坐标变换的方法简化DFIG的数学模型。

2.两相同步旋转坐标系上的数学模型

将三相静止坐标系下电机模型转化为两相同步旋转坐标系上的数学模型的等效原则是：在不同的坐标系下产生的磁动势相同。可以有两种方法进行变换，一种是在功率不变的约束条件下进行，另一种是在绕组匝数不变的约束条件下进行，两种方法的变换矩阵不同，变换后基本方程的形式大致相同（参数数值大小不同），区别是电磁转矩表达式的系数不同，采用功率不变的约束条件时，电磁转矩表达式的系数是1，采用绕组匝数不变的约束条件时，电磁转矩表达式的系数是1.5。本书采用绕组匝数不变的约束条件（见第一章第四节）。

基于坐标变换，建立两相同步旋转坐标系上的双轴数学模型为（依然按电动机惯例，见图8-26）。

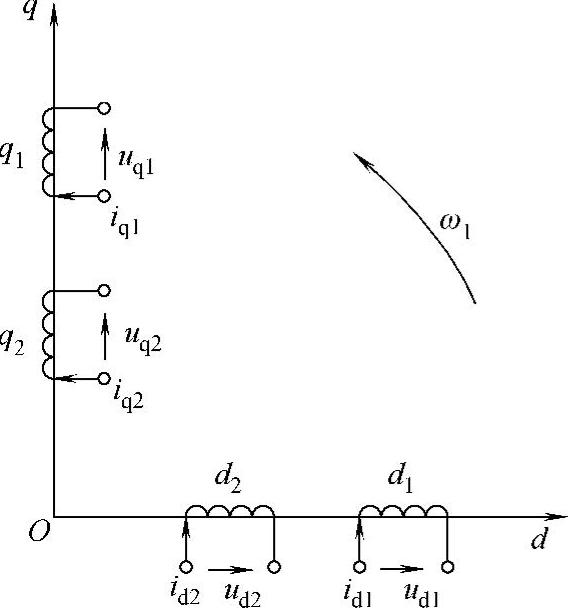
图8-26 两相同步旋转d-q坐标系下双馈发电机的物理模型

（1）电压方程式

式中 u_d1、u_q1、u_d2、u_q2——定、转子上d-q轴的电压分量；

i_d1、i_q1、i_d2、i_q2——定、转子上d-q轴的电流分量；

ψ_d1、ψ_q1、ψ_d2、ψ_q2——定、转子上d-q轴的磁链分量；

ω₁——定子旋转磁场角速度；

ω_s——转差角速度，且有

ω_s＝sω₁ （8-22）

（2）磁链方程式

式中 L₁——d－q坐标系等效两相定子绕组的自感；

L₂——d－q坐标系等效两相转子绕组的自感；

L_m——d－q坐标系同轴等效定子与转子绕组间的互感。(www.xing528.com)

把磁链方程的表达式带入电压方程表达式，得出矩阵形式

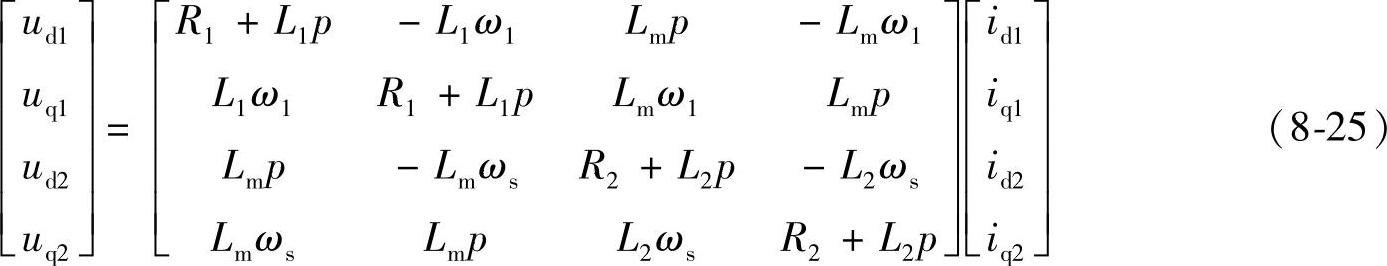
（3）转矩方程。经坐标变换后化简得

M_e＝1.5pL_m（i_q1i_d2－i_d1i_q2） （8-26）

（4）运动方程。与三相静止坐标系下相同。

式（8-21）、式（8-23）、式（8-26）和运动方程是电动机在两相同步旋转坐标系上的数学模型。由于d-q坐标系两轴互相垂直，之间没有互感的耦合关系，当三相静止坐标系中的电压和电流是对称正弦交流时，等效的两相变量是直流，便于控制。

将发电机定子上的有功功率P₁和无功功率Q₁用d-q坐标系上的分量表示，则有

3.定子磁链定向矢量控制

在矢量控制技术中，常采用定子磁链定向、转子磁链定向（用于感应电动机）和气隙磁链定向（用于同步电动机）等方法，为了简化有功功率和无功功率的计算，双馈发电系统采用定子磁链定向技术，控制系统相对简单。定向矢量图见图8-27。

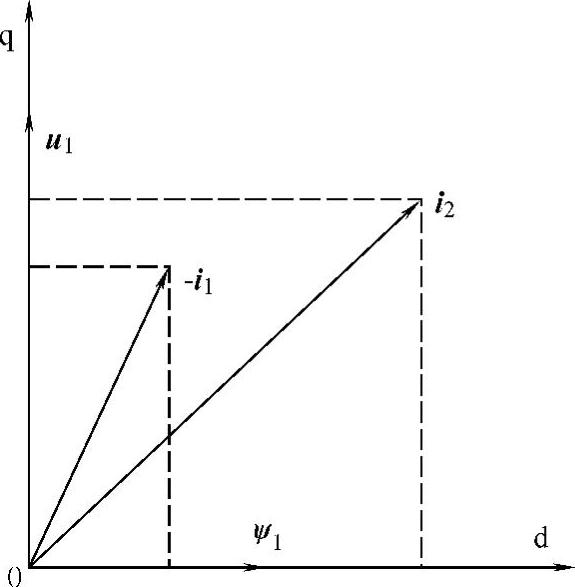
图8-27 定子磁链定向矢量图

按定子磁链定向规则，有

由式（8-23）可得：

于是得

忽略定子电阻（R₁≈0），对电动机惯例来说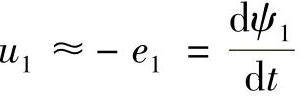，。那么相电压矢量将比磁链矢量超前90°，正好落在q轴的正方向上。由于定子接于恒定的电网上，电压综合矢量将是常数，保持不变的。所以有

则电压方程变为

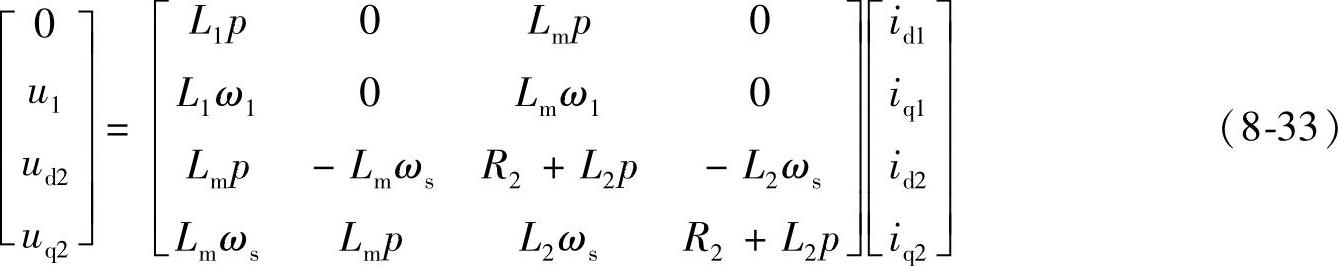
由式（8-29）和式（8-33）可得

pψ₁＝0 （8-34）

可见定子磁链也是恒定不变的。

根据转矩方程M_e＝1.5pL_m（i_q1i_d2－i_d1i_q2），把式（8-30）、（8-31）代入得

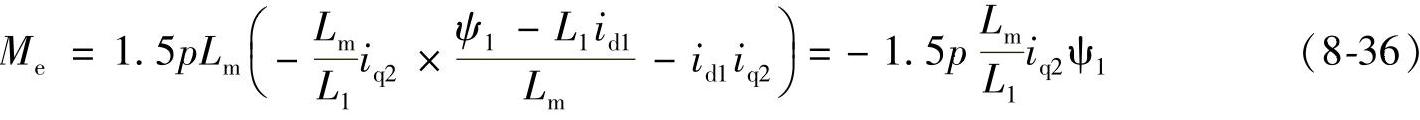
由式（8-36）可看出，在定子磁势保持不变的情况下，电磁转矩只与转子电流q轴分量有关。

将电压和电流的计算结果代入式（8-27）可得

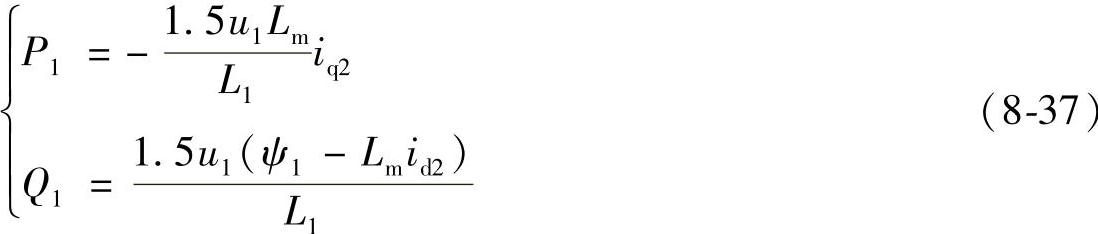
当风力发电机并入电网后，定子电压u₁恒定，ψ₁也不变。由式（8-37）可知，定子有功功率P₁只与转子励磁电流分量i_q2有关，无功功率Q₁只与转子励磁电流分量i_d2有关。这就实现了有功功率和无功功率的解耦控制。

由式（8-30）、（8-31）和转子侧电压方程，得

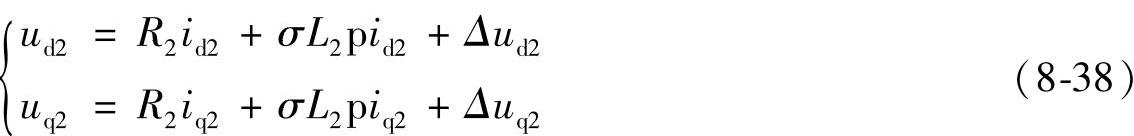
其中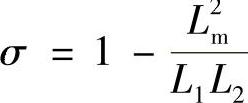

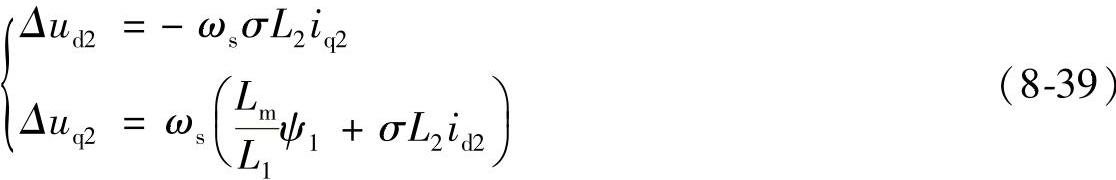
式（8-38）中的前两项为实现转子电压、电流解耦控制的解耦项，Δu_d2和Δu_q2为消除转子电压、电流交叉耦合的补偿项。这样将转子电压分解为解耦项和补偿项后，既简化了控制，又能保证控制的精度和动态响应的快速性。

4.定子磁链定向中的坐标变换和磁链观测

简化为同步旋转坐标系后的表达式虽然简单，但坐标变换和磁链观测也是很重要的一部分。通过静止两相坐标系下的测量值，估算定子磁链ψ₁的分量为

ψ_α1＝L₁i_α1＋L_mi_α2

ψ_β1＝L₁i_β1＋L_mi_β2 （8-40）

再通过矢量分析器得到旋转坐标系角度θ₁，计算公式如下

用旋转编码器可以检测到电机转子旋转角速度，积分后得到转子静止坐标系位置角θ₂，(θ₁－θ₂)与转子转差频率有关。

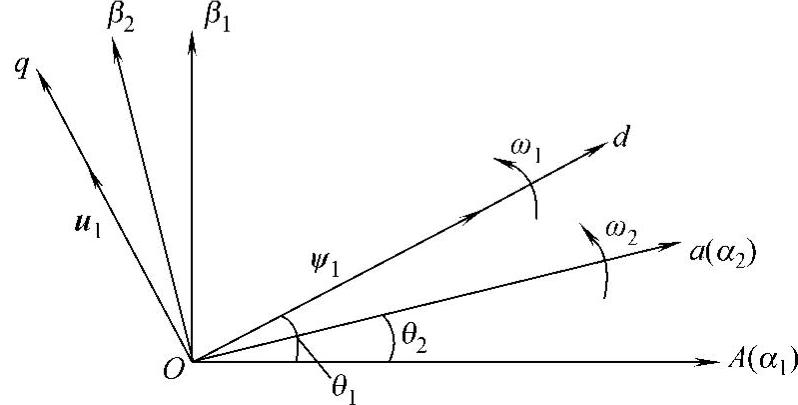
图8-28 坐标变换示意图

检测到的定子瞬时电流电压值，通过三相／两相静止坐标变换后，观测出定子磁链和旋转坐标系角度θ₁，检测到的转子瞬时电流值，通过三相／两相静止坐标变换后，变化角度为(θ₁－θ₂)，输送到控制单元（坐标变换示意图见图8-28）。

双馈发电机可以实现有功、无功功率的调节，按照风力发电机的转速功率输出曲线，给定不同的风速、发电机转速情况下的功率输出目标，额定风速以下以最佳叶尖速度比运行，额定风速以上，以限制功率输出方式运行。有功功率决定于转子侧励磁电流q轴分量大小，无功功率决定于转子侧励磁电流d轴分量大小，经过控制算法，给定转子侧励磁电流、电压大小d、q轴分量，经过旋转坐标系变换后，转换为静止坐标系下a、b、c分量，再通过PWM输出，控制框图如图8-29所示。