外转子永磁风力发电机数学模型解析

为分析简化起见，略去一些次要因素，作如下假设：

（1）忽略铁心饱和效应；

（2）不计涡流和磁滞损耗；

（3）转子上没有阻尼绕组，永磁体也没有阻尼作用；

（4）反电动势是正弦的。

根据以上假设，由永磁体产生的电动势E_g为

E_g＝2πf_eΦ （7-1）

式中 Φ——转子永磁体在定子相产生的磁通；

f_e——电频率，单位为Hz。

电频率计算公式为

f_e＝pf_m （7-2）

式中 p——极对数。

f_m——机械频率，单位为Hz。

在d－q轴坐标系中建立旋转坐标轴d－q轴数学模型，取永磁体基波磁场方向（即永磁体转子极中心线）为d轴，q轴为沿转子旋转方向超前d轴90°电角度。永磁励磁磁链与d轴重合，i为转子等效励磁电流，二极永磁发电机示意图如图7-9所示。

永磁同步发电机的电压和电磁转矩在d—q轴旋转坐标系下的数学关系为（按电动机惯例）

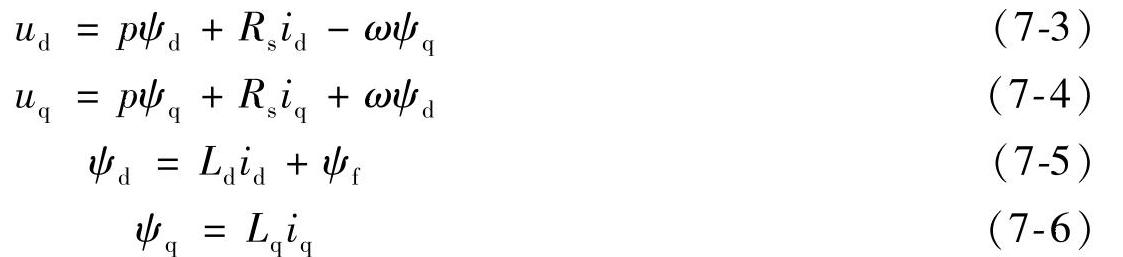
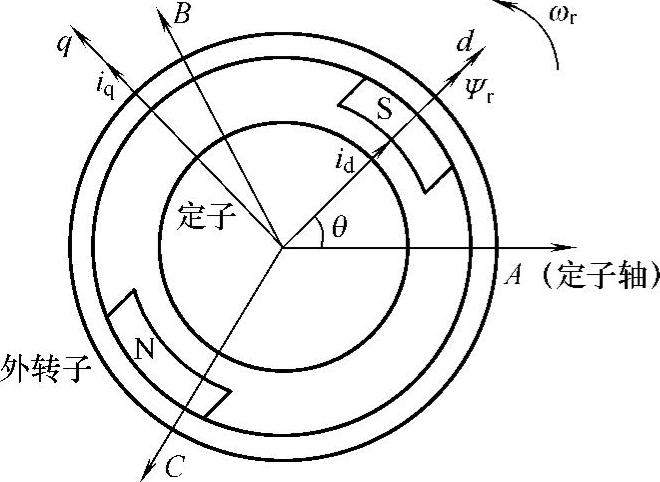
图7-9 二极永磁发电机示意图

式中 u_d、u_q——分别为d、q轴电压分量；

i_d、i_q——分别为d、q轴电流分量；

L_d、L_q——分别为d、q轴电感分量；(www.xing528.com)

ψ_α、ψ_a——分别为d、q轴磁链分量；

R_s——定子相电阻；

ψ_f——永磁体基波励磁磁场对定子绕组磁链；

ω——电气角速度；

p——微分算子。

发电机电磁转矩方程为

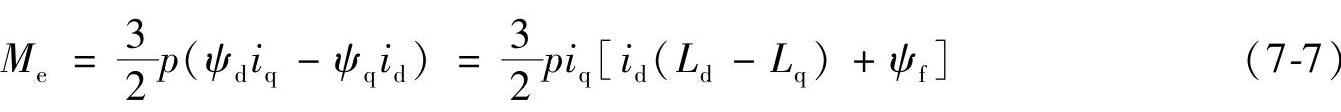
运动方程为（以转子旋转方向为正）

式中 M_m——风力机的机械转矩；

M_e——永磁电机电磁转矩；

J——永磁电机转动惯量；

Ω_m——机械角速度；

p——极对数。

在转子参考坐标系中，若取d轴的反方向为虚轴，取q轴为实轴，则在这个复平面内，可将定子电流空间矢量i_g表示为

i_g＝i_q－ji_d （7-10）

i_g与d轴间角度为β，于是i_d＝i_gcosβ，i_q＝i_gsinβ代入式（7-7）得到

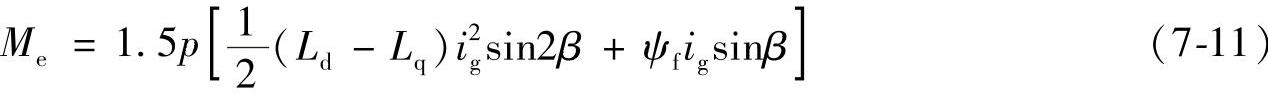
实际上，采用外转子结构与传统的内转子电机的工作原理是一致的，从式（7-11）可以看出，发电机的电磁转矩取决于定子电流空间矢量i_g。即对i_g控制来实现对发电机的控制。