折算法及求法分析

根据前面的分析，可以列出变压器负载运行时的基本方程组如下

利用这组联立方程式，便能对变压器进行定量计算。例如，当给定U₁，知道变压器的变比k和参数Z₁、Z₂、Z_m以及负载阻抗Z_L时，就能从上述六个方程式中解出六个未知量：I₁、I₂、I_m，E₁、E₂和U₂。但是，解联立复数方程组（2-10）是相当繁杂的；并且，由于电力变压器的电压比k较大，使一、二次电流、电压、阻抗等相差很大，计算时不方便，也不便于比较，特别是画相量图更是困难，因此引入了折算法。这是一种处理问题的方法，其目的是为了简化定量计算和得出变压器一、二次侧有电的联系的等效电路。

在变压器中，常常是把二次绕组折算到一次绕组，当然也可以相反。所谓把二次绕组折算到一次绕组是指：在进行定量计算时，把二次绕组的匝数变换成一次绕组的匝数，而不改变其电磁本质。这时变压比k等于1，主磁通感应于一、二次绕组的电动势相等，因而，使计算大为简化，并便于导出等效电路。这种折算后，二次侧各物理量的数值称为二次侧折算到一次侧的折算值，用原来的二次侧各物理量的符号加上一个“′”来表示。

在变换中，应做到把二次绕组的匝数变换成一次绕组的匝数，而不改变其电磁本质。从全电流定律，即从电流产生磁场的基本规律来看，只要在实行变换后，二次绕组的磁动势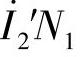及其空间分布情况和原来的磁动势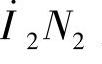完全一样，则变压器中的主磁通以及一、二次绕组的漏磁通的数量和空间分布的情况将和变换前的完全一样，因此，就不会改变变压器中的电磁本质。显然，这种折算对一次侧各物理量将毫无影响。一次侧将仍从电源吸取同样大小的功率和电流，并有同样大小的功率传给二次侧。下面根据上述概念导出折算值的求法。

1.二次电流的折算值

根据折算前后二次磁动势F₂不变的原则，可得

即

于是，式（2-4）变成了

上式表明，本来是磁路中的磁动势方程式F_m＝F₁＋F₂，经折算后，变成了电路中的电流方程式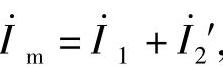，这样，电路和磁路之间通过电磁感应紧密联系在一起的变压器转化成纯电路来研究。

2.二次电动势的折算值

由于折算前后主磁场和漏磁场都没有改变，根据电动势和匝数成正比关系，便得

即

3.二次阻抗的折算值(www.xing528.com)

根据漏电抗定义可得

4.二次绕组电阻的折算值

由于折算后二次绕组的匝数从N₂变为N₁，但不改变其空间位置和几何尺寸，则每节导线的断面积应变为原来的N₂／N₁倍，而绕组导线总长度则变为原来的N₁／N₂倍，这样根据导线电阻与其长度成正比，而与其断面积成反比，可得

随之可得

5.二次侧电压的折算

从折算后二次绕组的端电压仍应等于主磁通感应的电动势减去二次绕组的漏阻抗电压降，可得

6.负载阻抗的折算值

从阻抗为电压和电流之比可得

综合以上所述可见，当把二次侧各物理量折算到一次侧时，凡是单位为V的物理量（电动势、电压等）的折算值等于其原来的数值乘以k；凡是单位为Ω的物理量（电阻，电抗，阻抗）的折算值等于其原来的数值乘以k²；电流的折算值等于其原来的数值乘以1／k。

从能量关系看，折算后绕组的铜耗为

输出的视在功率为

仍和折算前一样，没有改变。这是由于折算时保证了二次磁动势F₂不变，随之，F₁也不变，故主磁通和一、二次绕组的漏磁通都不变，因而能量关系不会改变。折算后，方程组（2-10）便成为