变压器与交流电机中的基本方程式

在变压器和交流电机中，电压、电流、电动势和磁通等物理量的大小及方向都随时间改变，为了正确地表示它们之间的数量和相位关系，在列方程式时，必须首先规定各物理量的正方向。正方向原则上可以任意规定，但是正方向规定的不同，同一电路内所列方程式中各物理量的正负符号不同。为了避免出错，采取下述的统一规定。

1）在作为负载的电路里（相当于电动机），外加电压是电源，在外加电压的作用下，电路内才产生电流，所以，先规定外加电压的正方向，再取电流的正方向与电压的正方向一致；对纯电阻负载来说，就是正电压产生正电流。

2）当电流产生磁通时，磁通的正方向和电流的正方向符合右手螺旋关系，就是说，正电流产生正磁通。

3）在电磁感应中，磁通的正方向和由它感应的电动势的正方向符合右手螺旋关系，这时电磁感应定律的表达式是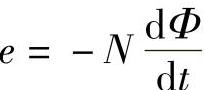。把第二条和第三条规定结合在一起便得：在电流产

图2-14 变压器的负载运行

生磁通，磁通感应电动势的情况下，电动势的正方向和电流的正方向取得一致。

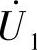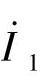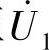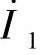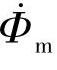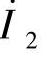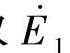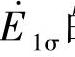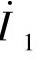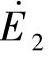按上述的正方向规定原则，可得变压器负载时各物理量的正方向的规定法，如图2-14所示。对于电源来说，一次绕组是负载，因此，首先选定一次电压的正方向，即由A点至X点：电流的正方向取得与电压的正方向一致，即由A点经一次绕组至X点。从电流的正方向，按右手螺旋关系确定主磁通的正方向为顺时针方向；再从主磁通正方向，按右手螺旋关系定出二次绕组电流的正方向，由a点经二次绕组至x点；于是，利用上述的电流和电动势正方向取得一致的原则，可取和的正方向和的一致，和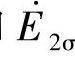的正方向则和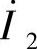的一致。这时，从变压器二次侧来看，二次绕组是“电源”，阻抗Z_L是“负载”，在电动势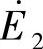的作用下，二次侧才产生电流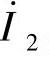，其正方向从x点经负载至a点，由此二次电压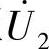的正方向应为从x点至a点。

上述正方向的规定方法，也适合于变压器中能量传递规律。由于u₁和i₁正方向一致，当u₁和i₁同时为正或负时，一次侧都从电源输入电功率u₁i₁。由于u₂和i₂的方向一致，当u₂和i₂同时为正或负时，二次侧都向负载输出电功率u₂i₂。

1.磁动势平衡方程式

在变压器中，由于一次磁动势F₁和二次磁动势F₂都作用在同一磁路上，在图2-14中，按全电流定律，可得变压器负载运行时的磁动势方程式为

F₁＋F₂＝F_m （2-3）

上式表明，负载运行时，变压器的合成磁动势F_m是一次磁动势F₁和二次磁动势F₂的矢量和。负载时的主磁通是由合成磁动势F_m建立的。如果用一次绕组的电流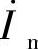所产生的磁动势来代替合成磁动势，即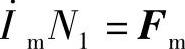，则磁动势方程式可写成

式中 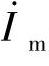——励磁电流。(www.xing528.com)

将式（2-4）两边除以N₁，便得

或

式中 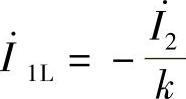——一次电流的负载分量。

上式表明，变压器负载运行时，一次电流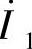有两个分量，一个是励磁电流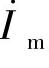，用于建立变压器负载运行时的主磁通；一个是负载分量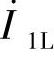，产生磁动势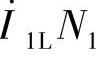，用于抵消二次侧磁动势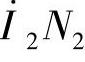，即

这与分析变压器负载运行时的物理情况所得结论相同。

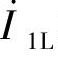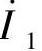式（2-6）称为磁动势平衡关系，是分析变压器性能时经常用到的一个重要关系式。在忽略励磁电流时，式中的就用代替。

顺便指出：由于变压器一次绕组的漏抗电压降很小，故从空载到额定负载时，E₁变化很小，与之相对应的主磁通和产生主磁通的合成磁动势F_m变化也很小，所以，负载时的励磁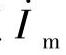电流与空载电流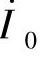相差很小，可以近似地认为相等。

2.电动势平衡方程式

变压器负载运行时，除了主磁通在一、二次绕组中感应的电动势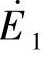和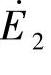外，还有仅与一次绕组交链的漏磁通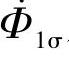所感应的漏磁电动势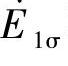和仅与二次绕组交链的漏磁通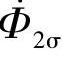所感应的漏磁电动势。

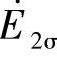一次侧漏磁电动势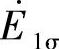可用漏电抗电压降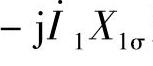来代替，其中X_1σ是一次绕组的漏电抗，是一常数。同样，二次侧漏磁电动势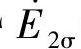也可用漏电抗电压降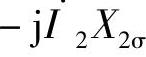来代替，式中X_2σ称为二次绕组漏电抗，也是常数。再考虑到一、二次绕组有电阻R₁和R₂，按图2-14所规定的各物理量的正方向，利用电路定律，便可写出变压器负载运行时一、二次电动势平衡方程式如下

式中 Z₁＝R₁＋jX_1σ、Z₂＝R₂＋jX_2σ是一、二次绕组的漏阻抗，均为常数，与电流大小无关。

上述的磁动势平衡方程式和电动势平衡方程式概括了变压器中的电磁关系，称为变压器的基本方程式。