K-S检验法（D检验法）及其应用

当试验次数n较少时，可以采用K-S检验法进行分布的拟合优度检验。K-S检验法是通过将样本的经验分布函数Fn（x）（或者F′n（x），通常选择为累积分布函数）与指定的分布函数Fn（x）进行比较，计算它们在垂直方向上的最大距离Dn。若Dn小于某一给定的值，说明Fn（x）与F0（x）吻合得较好，否则说明Fn（x）与F0（x）之间存在较大的差异。K-S检验法的原理如图4-4所示。

图4-4　K-S检验法的原理

运用K-S检验法进行分布拟合优度检验的过程如下：

（1）将样本试验结果的观测值按照从小到大的顺序排列，排序结果记为x（1），x（2），…，x（n）。

（2）计算累积分布函数，选择和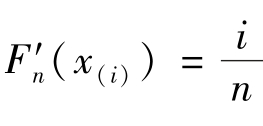两种累积分布函数，其中i=1，2，…，n。

（3）计算Kolmogorov检验统计量Dn，取

按照格里汶科（Glivenko）定理，在H0成立的条件下，当n趋于无穷大时，Dn在概率意义上无限趋近于零（即Dn依概率1收敛于0），用公式表示为

（4）对于给定的显著性水平α，查Kolmogorov检验表（表4-2），选择dα（n），若Dn>dα（n）则拒绝H0，否则接受H0。

对于检验中存在未知参数的情况，可先估计参数，再进行假设检验。

从表4-2可见，仅给出了n≤100的临界值dα（n）。当n>100时，可采用χ2检验法，或运用如下方法进行检验：

表4-2　Kolmogorov检验表（P（Dn≤dα）＝1-α）

定义分布函数K（x）

若F0（x）连续，在H0成立的条件下，n→∞时的分布收敛于分布K（x）（即依分布收敛于K（x））。用数学公式表示为

这样，利用K（x）就可以确定大样本时拒绝域的临界值。(www.xing528.com)

对于给定的α，表4-3中给出的λα满足：

当n>100时，计算Dn后，可进行如下判断：

若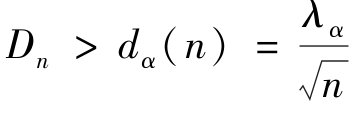，则拒绝H0；

若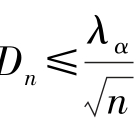，则接受H0。

表4-3　Kolmogorov统计量Dn的极限分布K（λ）

表中，。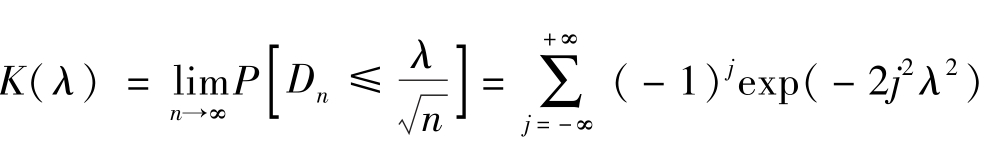

【例4-4】在对某装备的MTBF检验中，抽取10件产品进行试验，得到试验数据为：2.427 2，1.166 4，0.407 1，1.517 7，8.678 8，4.510 6，0.333 5，0.433 8，4.454 7，0.562 2（单位：1 000 h），在置信水平1-α=0.95的条件下，检验该产品的寿命是否服从指数分布。

解：按照K-S检验的步骤计算MTBF的估计，得到其估计值，则假设检验转化为：

H0：F（x）服从MTBF=2.449 2的指数分布，

H1：F（x）不服从MTBF=2.449 2的指数分布。

首先对数据进行排序，得到：0.333 5，0.407 1，0.433 8，0.562 2，1.166 4，1.517 7，2.427 2，4.510 6，4.454 7，8.678 8。

分别计算及Dn，则得Dn为

查表4-2，可得d0.05（10）=0.409 25，Dn>dα（n），所以拒绝H0，即在置信水平1-α=0.95的条件下，不能接受原假设。