被测对象仅有两种状态：一种是正常状态

1.基本假设

（1）被测对象仅有两种状态：一种是正常状态，UUT无故障可以正常工作；另一种是故障状态，UUT不能正常工作。

（2）在任何时刻当UUT处于故障状态时，认为只有一个组成单元（或部件）发生了故障，即单故障假设。即使UUT同时存在两个以上的故障（概率很小），实际诊断时也是逐个隔离较为简便。

（3）被测对象的状态完全取决于其各组成单元的状态。某一组成单元发生了故障，在信息流可达的各个测试点上，测量有效性都是一样的。

2.定义

1）测试和测试点

（1）测试。为了确定被测对象的状态并隔离故障所进行的测量与观测的过程称为测试。测试过程中可能需要激励和控制，观测其响应，如果其响应是所期望的，则认为正常，否则认为故障。

（2）测试点。进行测试时，可以获得所需状态信息的任何物理位置称为测试点。

一个测试可以利用一个和数个测试点，一个测试点也可被一个或多个测试利用。为便于理解，开始时可以认为一个测试就使用一个测试点，则测试点就代表了测试，用Tj表示测试或测试点。

2）被测对象的组成单元和故障类

（1）被测对象的组成单元。被测对象的组成部件，不论其大小和复杂程度，只要是故障隔离的对象，修复时要更换的，就称为组成单元。

（2）故障类。实际上，诊断分析真正关心的是组成单元发生的故障，所以组成单元可以用所有故障来代表，它们具有相同或相近的表现特征，称为故障类。

为了便于理解，在以后测试点的选择和诊断顺序分析中用Fi表示组成单元、组成部件或组成单元的故障类。(www.xing528.com)

3）相关性

相关性是指被测对象的组成单元和测试点之间、两个组成单元之间或两个测试点之间存在的逻辑关系。例如，若测试点Tj依赖于组成单元Fi，当Fi发生故障时，则意味着Tj测试结果应是不正常的。反过来，如果Tj测试通过，则证明Fi是正常的，这就表明Tj与Fi是相关的。仅表明某一个测试点与其输入组成单元（1个或n个），以及直接输入该组成单元的任何测试点（1个或几个）的逻辑关系，称为一阶相关性模型。如果表明了被测对象的各个测试点与各个组成单元之间的逻辑关系，则称为高阶相关性模型。

3.相关性图示模型

相关性图示模型是在UUT功能和结构合理划分之后，在功能框图的基础上，清楚地标明功能信息流方向和各组成部件相互连接关系，并标注清楚初选测试点的位置和编号，以此表明各组成部件与各测试点的相关性关系，如图3-45所示。其中，方框代表各个功能单元，圆圈代表测试点，箭头表明了功能信息传递的方向。

图3-45　相关性图示模型

4.相关性数学模型

UUT的相关性数学模型可以用下述矩阵表示：

其中第i行矩阵为

表示第i个组成单元（或部件）故障在各测试点上的反应信息，它表明了Fi和各个测试点Tj（j=1，2，…，n）的相关性。而第j列矩阵为

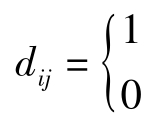，表示第j个测试点可测得各组成部件的故障信息。它表明了Tj与各组部件Fi（i=1，2，…，m）的相关性。其中：

UUT的相关性数学模型也称为D矩阵模型，如图3-46所示。

图3-46　相关性数学模型