RC电路时间常数的计算与应用

把uC和i不同时刻的数值列于表4-2中,可见换路后经过一个τ的时间,uC衰减为初值U0的36.8%。换句话说,uC衰减到原值36.8%所经历的时间是一个时间常数τ。

从理论上讲,需要经历无限长的时间电压才衰减到零,电路才能达到稳定状态,但实际工程上一般认为,只要经过(3～5)τ的时间,电压就已经衰减到忽略不计了,这时可认为过渡过程基本结束。显然动态过程的快慢是由时间常数的大小来决定的。时间常数越小,衰减过程越快,反之时间常数越大,衰减过程越慢。

表4-2　uC和i不同时刻的数值

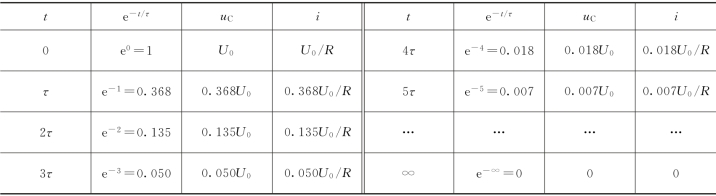
【例4-4】 在图4-12(a)中,R=2Ω,C=1μF,I=2A,uC(0)=U0=1V。试求t≥0时的uC、iC和iR,并作出变化曲线。

解:本例可应用戴维南定理计算,换路后的等效电路如图4-12(c)所示。等效电源的电动势和内阻分别为

E=RI=2×2=4(V)

R0=R=2Ω

电路的时间常数为

τ=R0C=2×1×10-6=2×10-6(s)

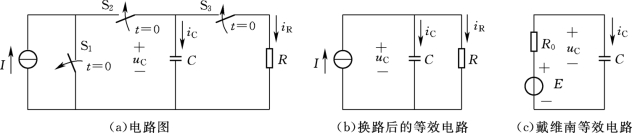
图4-12　[例4-4]图

根据式(4-11)得

由此得

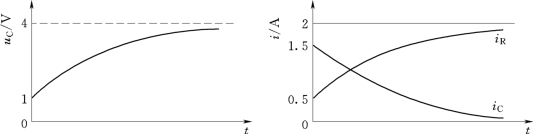
所求uC、iC和iR的变化曲线如图4-13所示。

(www.xing528.com)

图4-13　uC、iC和iR的变化曲线

【例4-5】 在图4-14中,U=20V,C=4μF,R=50kΩ。在t=0时闭合S1,在t=0.1s时闭合S2,求闭合后的电压uR。设uC(0-)=0。

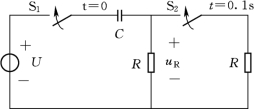
图4-14　[例4-5]图

解:在t=0时闭合S1后,得

其中　τ1=RC=50×103×4×10-6=0.2(s)

在t=0.1s时

在t=0.1s时闭合S2后,可应用三要素法求uR:

(1)确定初始值。

uR(0.1s)=12.14V

(2)确定稳态值。

uR(∞)=0

(3)确定时间常数。

于是可写出