换路定则及初始值的优化策略

1.换路定则

电路的接通、切断、短路、电动势幅值、波形的突变、电路连接方式及电路参数的突然改变等统称为换路。

换路定则是指一个具有储能元件的网络中,在电路换路瞬间,电感元件的电流不能突变,电容元件的端电压不能突变。

从能量观点来看换路定则是容易理解的。我们知道,电感的磁场能量WL=电容的电场能量WC=式中电感量L和电容量C都是常量。假设电感中电流IL可以突变,则电感元件储存的磁场能量WL也要发生突变,磁场能量的突变意味着电源提供的功率P==∞。事实上,没有能在瞬间提供无限大功率的电源,这说明了电感元件中电流的突变是不可能的。同理,如果假设电容端电压UC可以突变,则电容元件储存的电场能量WC也要发生突变,用同样道理可以说明电容电压的突变也是不可能的。

如果取时间t=0为换路瞬间,以t=0-表示换路前的终了瞬间,t=0+表示换路后的初始瞬间,则换路定则可叙述如下:

从t=0-到t=0+换路瞬间,电感元件中的电流和电容元件上的电压保持原值不变。即

式(4-1)和式(4-2)称为换路定则。

2.初始值的确定

任意一个二端网络,在其输入端加电压或电流信号,此信号称为激励。在激励的作用下,该二端网络的各个元件上将产生相应的电流或电压,此电流或电压称为响应。

电感元件的初始电流iL(0+),以及电容元件的初始电压uC(0+),是一组独立的初始值。所谓独立就是说该初始值不能用其他初始条件推导出来,而网络中任何其他初始条件和响应,都可以用电感电流的初始值和电容电压的初始值以及激励来表示。

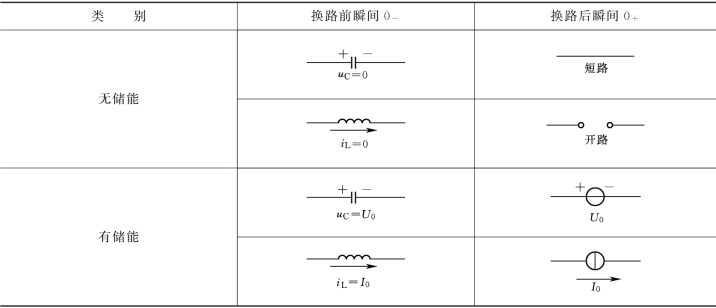
确定初始值的方法可画出0+时刻的等效电路,再用计算稳态电路的方法求出所需要的其他非独立的初始值。储能元件0+等效电路见表4-1的直观说明。

表4-1　储能元件0+等效电路

【例4-1】 电路如图4-2所示,开关S原来打开,电容和电感都没有储能,t=0时,开关S闭合,求开关闭合后初始瞬间电容中电压和电感中电流的初始值。

解:(1)求图4-2(a)电路在开关闭合后电压和电流的初始值。

由于t=0-时开关S断开,且电容没有储存电荷,故

iC(0-)=0,uC(0-)=0,uR(0-)=0

根据换路定则

uC(0+)=uC(0-)=0

因uC(0+)=0,所以t=0+瞬间,电容C相当于短路,该瞬间的等效电路如图4-3(a)所示,由图可知

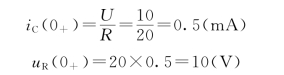
这个计算结果表明,电容元件的电流和电阻元件端电压是可以跃变的。

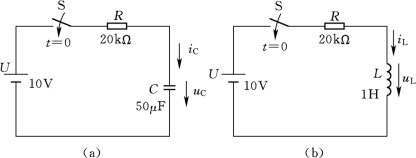
图4-2　[例4-1]的电路图(www.xing528.com)

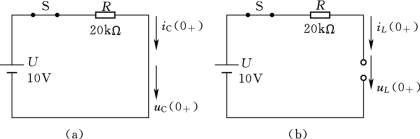
图4-3　图4-2在t=0+时的等效电路图

(2)求图4-2(b)电路在开关闭合后电压和电流的初始值。

由于t=0-时开关S是断开的,且电感没有电流,故

iL(0-)=0,uL(0-)=0,uR(0-)=0

根据换路定则

iL(0+)=iL(0-)=0

因iL(0+)=0,所以t=0+瞬间,电感相当于开路,该瞬间的等效电路如图4-3(b)所示,由图可知

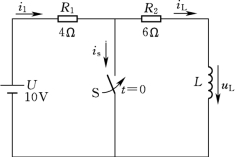
图4-4　[例4-2]的电路图

uL(0+)=U=10(V)

uR(0+)=0(V)

uL(0+)=10V表明电感元件端电压是可以跃变的。

【例4-2】 在如图4-4所示电路中,电路原已处于稳态,在t=0时S闭合,求电路中各元件的电压和电流的初始值。

解:(1)求出t=0-时电路中各电流、电压值。

由于S闭合前电路已处于稳态,故在t=0-瞬间,电感相当于短路,等效电路如图4-5(a)所示,由图可知

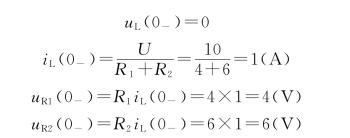
(2)求t=0+时电路中各电流、电压值。根据换路定则

iL(0+)=iL(0-)=1A

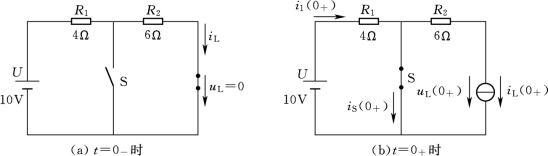
图4-5　图4-4电路的等效电路

由于iL(0+)=1A,所以在t=0+瞬间电感相当于一个电流源,且S已闭合,等效电路如图4-5(b)所示。由图可知

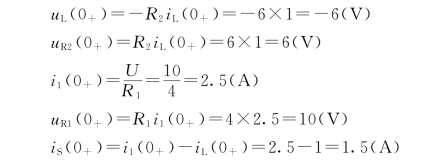
由以上两例计算结果可见,电容电压和电感电流在换路瞬间不能突变,但电容电流和电感电压在换路瞬间是可以突变的,而电阻的电压和电流也是可以突变的。