有时根据负载的工作要求,负载需要进行三角形连接,如图3-10所示。图中分别规定了线电流![]() 与相电流
与相电流![]() 的参考方向。可以看出各相负载二端的电压等与电源的线电压,不论负载对称与否,每相负载两端电压都能保持对称关系。因此每相负载的相电流有效值可由下式计算得出:
的参考方向。可以看出各相负载二端的电压等与电源的线电压,不论负载对称与否,每相负载两端电压都能保持对称关系。因此每相负载的相电流有效值可由下式计算得出:

各相电流与相应电压的相位差为

式中:RAB、RBC、RCA、XAB、XBC、XCA为各相负载的电阻与电抗。
据基尔霍夫电流定律,由图3-10可建立相电流与线电流的关系,即

如果负载不对称,则电压、电流则按上述公式逐项计算。
如果负载对称,根据式(3-13)可知各相电流的数值相等,而且各相的相电流与相应的相电压之间有相同的相位差φ。其相量图如图3-11所示,可见三个相电流也是对称的。
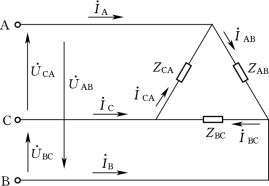
图3-10 负载的三角形解法
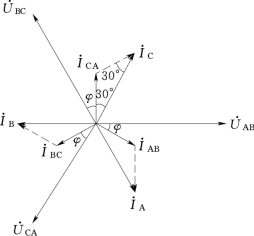
图3-11 三角形对称负载相量图
根据图3-11可得知线电流与相电流的大小关系为

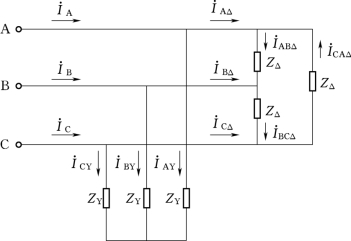
图3-12 [例3-3]的电路图
由式(3-16)可知,当对称负载作三角形连接时,线电流IL是相电流IP的![]() 倍,且由图3-11知滞后对应相电流30°,即
倍,且由图3-11知滞后对应相电流30°,即

【例3-3】 在图3-12所示的380/220V三相电路中,有二组对称负载分别以三角形和星形接入。按星形接入的每相负载ZY=3+j4Ω,三角形接入的每相负载ZΔ=6-j4Ω,求iA、iB、iC。
解:(1)星形接法复阻抗
ZY=3+j4=5∠53.1°(Ω)
以A相电压![]() 为参考相量,A相电流为
为参考相量,A相电流为

因负载对称,![]() 幅值相等,只是相位互差120°,所以
幅值相等,只是相位互差120°,所以

在星形接法中,相电流等于线电流。
(2)三角形接法复阻抗
ZΔ=6-j4Ω=7.2∠-33.7°(Ω)(https://www.xing528.com)
以![]() 为参考相量,则
为参考相量,则

因负载对称,则B、C二相的相电流为
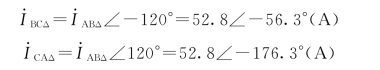
三角形对称负载线电流是相应相电流的![]() 且在相位上滞后30°,则有
且在相位上滞后30°,则有

根据基尔霍夫电流定律得
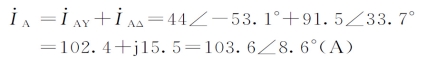
因负载对称,则有

各线电流的瞬时值表达式为
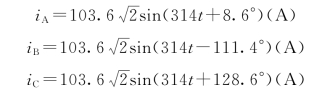
【例3-4】 设有额定功率PN=100W,额定电压UN=220V的白炽灯共14盏,三角形连接,接在线电压为220V的三相电源上。若A、B相线间接6盏,B、C相线间接3盏,C、A相线间接5盏,试求各相电流和线电流。
解:由于各相所接白炽灯数量不同,则负载阻抗就不对称。因此,各相电流及线电流就必须一相一相地单独计算。
设
![]()
每盏电灯的电阻
![]()
则A、B相线之间的等效电阻
![]()
B、C相线之间的等效电阻
![]()
C、A相线之间的等效电阻
![]()
(1)相电流

(2)线电流
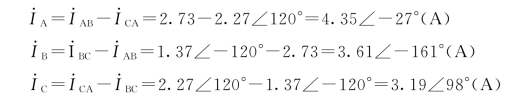
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




