在RLC并联电路中,当并联电路的电压与并联电路的总电流相位相同时称为并联谐振。并联谐振的结构形式很多,我们只选择比较典型的常用电路为例,对并联谐振的条件、特征和用途作一简要说明。
1.谐振条件
图2-28为所讨论的并联电路,其中线圈支路复阻抗ZL=RL+j XL,电容支路复阻抗ZC=-j XC。各支路电流为
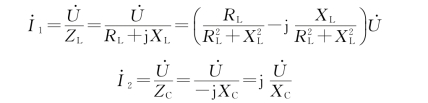
总电流

当并联电路发生谐振时,总电压和总电流应同相位,所以式(2-43)中电流的虚部分量应为零,即

经整理,可解出满足并联谐振的角频率为
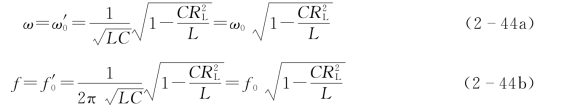
式中:![]() 为并联谐振的角频率;f'0为并联谐振的频率;ω0为串联谐振的角频率;f0为串联谐振的频率。
为并联谐振的角频率;f'0为并联谐振的频率;ω0为串联谐振的角频率;f0为串联谐振的频率。
在实际应用中,往往采用损耗较小的谐振回路,即电感线圈的电阻RL很小,故可近似认为

2.谐振特性(https://www.xing528.com)
(1)并联谐振时,电路阻抗很大,且为电阻性。由式(2-43)和式(2-44a)联合整理出电路的等效阻抗Z0=![]() 该阻抗的虚部为零,只有实数部分,电路呈电阻性,且RL很小,故Z0具有很高的数值,这与串联谐振电路的特征正相反。
该阻抗的虚部为零,只有实数部分,电路呈电阻性,且RL很小,故Z0具有很高的数值,这与串联谐振电路的特征正相反。
(2)电路中电流很小。谐振时,![]() 因Z0很大,故
因Z0很大,故![]() 很小。理想情况下RL等于零,等效阻抗Z0=
很小。理想情况下RL等于零,等效阻抗Z0=![]() 趋于无穷大,电路总电流
趋于无穷大,电路总电流![]() 等于零,各支路的电流为I1=
等于零,各支路的电流为I1=![]() I2=
I2=![]() 因谐振时
因谐振时![]() ,所以I1=I2。但
,所以I1=I2。但![]() 反相。这时电源无需向并联谐振电路提供电能,所以
反相。这时电源无需向并联谐振电路提供电能,所以![]() =0,而在谐振电路中仍存在电流
=0,而在谐振电路中仍存在电流![]() 这是因为原先储存的电场能量和磁场能量互相转换形成持续的往复振荡。在电流持续运动过程中,如果没有电阻,则此电流可以往复不已。综上所述,并联谐振回路中电感电流、电容电流可能远大于流入回路的总电流,因此,并联谐振又常称为电流谐振。
这是因为原先储存的电场能量和磁场能量互相转换形成持续的往复振荡。在电流持续运动过程中,如果没有电阻,则此电流可以往复不已。综上所述,并联谐振回路中电感电流、电容电流可能远大于流入回路的总电流,因此,并联谐振又常称为电流谐振。
3.谐振电路的应用

图2-29 并联谐振的应用
在电子技术和无线电工程中,常利用并联谐振时阻抗极高的特点,实现选频作用或消除干扰。如图2-29所示,有一恒流源接于LC并联谐振电路,因恒流源输出电流恒定,不随负载变化,故恒流源两端的电压即输出端电压随负载阻抗的增大而增大。若恒流源输出中包含各种不同频率的信号,而电路只对谐振频率的信号呈现出很高的阻抗,就可在恒流源的输出端得到很高的电压。电路对其他非谐振频率的信号,呈现阻抗很小,所以电压很低。这样在并联谐振电路的两端就可以把所需的频率信号选出来,而把其他频率信号抑制掉,起到选频的作用。
【例2-17】 有一电感线圈,电阻RL=20Ω,电感量L=0.3m H,和一电容量C=80p F的电容器并联,试求谐振频率和谐振阻抗。
解:若忽略电阻不计,谐振频率为
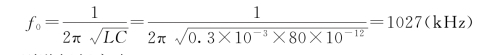
考虑电阻,则谐振频率为

由上面计算结果可见,因电阻值较小,故此对谐振率几乎毫无影响。
谐振时的阻抗为
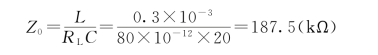
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




