如何优化电路的功率因数？

在交流电路中,有功功率P=UI cosφ,式中cosφ为电路的功率因数。前面曾提到,功率因数仅取决于电路(负载)的参数,对电阻性负载(例如白炽灯、电阻炉等)来说,由于电压、电流同相,其功率因数为1。除此之外,功率因数均介于0与1之间。在生产实际中,用电设备大多属于电感性负载。如电动机、电磁开关、感应炉、日光灯等,它们的功率因数比较低,交流异步电动机在轻载运行时,功率因数一般在0.2～0.3之间,在额定负载运行时,功率因数也只在0.8左右。

当电压与电流之间有相位差时,即功率因数不等于1时,电路中发生能量互换,出现无功功率Q=UI sinφ。这样就引起下面两个问题:①使发电设备的容量不能充分利用;②输电线路效率降低。

发电机(或变压器)有一定的额定容量,如SN=UNIN,发电机的电压和电流不容许超过额定值,所以发电机(或变压器)可提供的有功功率为P=UI cosφ,负载的功率因数cosφ越高,发电机可提供的有功功率越大,其容量就可以得到充分利用。如果cosφ很低,发电机发出的有功功率就很小,其容量就不能充分发挥。因为无功功率会增大,电路中能量互换的规模增大,即在发电机与负载之间进行互换。例如对于100k VA的发电机,当cosφ=0.9时,能发出900kW的有功功率;而当cosφ=0.6时,则只能发出600kW的有功功率。

当发电机的输出电压和有功功率一定时,I=即发电机通过输电线路向负载提供的电流I与功率因数cosφ成反比,而发电机绕组和线路中的功率损耗为

式中:RL为线路电阻和发电机绕组电阻的等效电阻。

显然,功率因数cosφ越大,所损耗的功率也就越小,输电效率也就越高。

从上述讨论可见,提高线路的功率因数既能提高发电设备的利用率,又能减少电能在输送过程中的损耗。这是一项节约能源和提高电能质量的重要措施,对国民经济的发展有着极为重要的作用。故此,电业部门规定:高压供电的工业企业的平均功率因数不低于0.95,其他单位不低于0.9。对于功率因数低于0.7的用户,不予供电;新通或新建的电力用户的功率因数不应低于0.9;对于功率因数不合要求的用户将增收无功功率电费。

提高功率因数的常用办法是在电感性负载的两端并联电容器,其电路图如图2-18(a)所示,这种电容器称为补偿电容。其基本原理可以简单叙述如下:

并联电路的相量图如图2-18(b)所示。并联电容器之前,感性网络中的电流(也是线路上的电流)落后于电压角度。如果将电容器并入感性网络后,线路上的电流不再是而是由感性网络电流与电容器电流的相量和,即而并联电容器以后,流入感性网络的电流I1=(Z=R+j XL表示感性网络的负载)和功率因数cosφ1=均未变化,这是因为所加电压和负载参数没有改变。从相量图看出,线路电流数值减小了,电源电压与线路电流间的相位差也减小到了φ2,从而整个网络的功率因数得到提高。

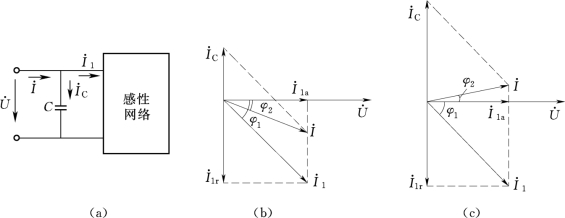
图2-18　电容器与感性负载并联以提高功率因数

采用并联电容器提高功率因数需要注意以下几点:

(1)并联电容器以后,不影响原来负载的正常工作。所谓提高功率因数,是指提高电源或电网的功率因数,不是指提高负载的功率因数。

(2)电容器本身不消耗功率。

(3)并联电容器以后,提高了功率因数,减少了电源与负载之间的能量互换。这时电感性负载所需的无功功率,大部分或全部都是由电容器就地供给,就是说能量的互换现在主要或完全发生在电感性负载与电容器之间,因而使发电机容量能得到充分利用。

由相量图2-18(b)可见(www.xing528.com)

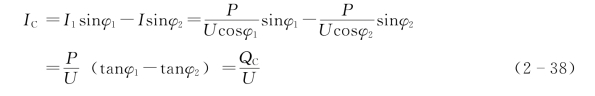
式中:QC为电容无功功率。

由于

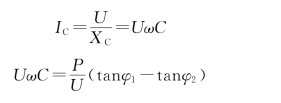
故有

【例2-11】 有一电感性负载,其功率P=10kW,功率因数cosφ1=0.6,接在电压U =220V的电源上,电源频率f=50 Hz。(1)如果将功率因数提高到cosφ2=0.95,试求与负载并联的电容器的电容值和电容器并联前后的线路电流;(2)如果要将功率因数从0.95再提高到1,试问并联电容器的电容值还需增加多少?

解:(1)cosφ1=0.6,即φ1=53°,cosφ2=0.95,即φ2=18°。

因此电容器的电容值为

并联电容器之前线路电流为

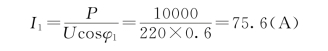
并联电容器之后线路电流为

(2)如果要将功率因数由0.95提高到1,则需要增加的电容值为

可见在功率因数已经接近1时再继续提高,则需要增加的电容值是很大的,成本会大大增加。