RLC串联电路中各电物理量的关系

由上所述可知,在RLC串联电路中,R、L、C可以看作三个阻抗元件相互串联,即Z1=R、Z2=j XL、Z3=-j XC,而Z可以看作串联电路的等效复阻抗:

Z=Z1+Z2+Z3=∑R+j∑X

式中:R为等效电阻;X为等效电抗,若感抗取正号,则容抗取负号。

如果以电流为参考相量=I∠0°),假定XL＞XC,则各电物理量之间的相量关系如图2-13(a)所示。图中,正好组成一个直角三角形。这一三角形称为电压三角形,如图2-13(b)所示。根据几何关系,可得

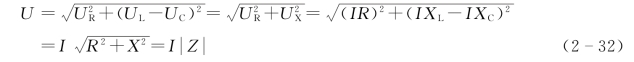
由相量图可以看出,由于总电压是各部分电压的相量和而不是代数和,因此,当电路中同时接有电容和电感时,总电压的有效值可能小于电容或电感电压的有效值,总电压小于某部分电压,这在直流电路中是不可能出现的。

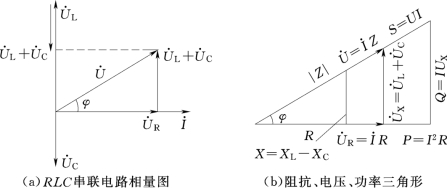
图2-13　RLC串联电路中各量的关系

若将电压三角形各边同除以电流I,即可得阻抗三角形,见图2-13(b)。

若将电压三角形每条边扩大I倍,则得

P=UI cosφ,Q=UI sinφ

RLC串联交流电路中因耗能元件只有电阻,其P=URI=I2R,根据电压三角形,可得

P=I2R=UI cosφ

电感元件与电容元件只存在无功功率Q,其中Q=I2XL,Q=I2XC,考虑到方向相反,得到

Q=(UL-UC)I=I2(XL-XC)=UI sinφ

斜边UI在交流电路中表示视在功率S,即

视在功率的单位是伏安(VA)或千伏安(k VA)。

许多交流电气设备,如交流发电机、变压器的容量就是以额定电压和额定电流的乘积,即用所谓的额定视在功率来表示的,记作

SN=UNIN

这样S、P、Q也组成一个三角形,称为功率三角形,如图2-13(b)所示。

在串联交流电路的分析和计算中,借助于电压、阻抗和功率三角形,可以十分直观地看出各电压、阻抗及功率之间的关系。

从这个三角形中,不难得出电源电压与电流之间的相位差,即

φ称为复阻抗的幅角或称为电路的阻抗角,它仅决定于电路参数和频率,与电压、电流无关。同时从三角形中还可看到

上述表达式在今后会经常用到。

需要注意的是:电压三角形、阻抗三角形、功率三角形虽是相似三角形,但各自代表的意义有着原则的区别。电压三角形各边代表相量,它实质是以相量图的形式来表示正弦量。而阻抗三角形、功率三角形各边只是线段,不带箭头,不是相量,它只反映出电路中的数值关系。

【例2-8】 一个电容器与线圈串联组成的电路中,外接电源电压为u=100sin(5000t)V。电容器的电容量C=10μF,线圈的电阻R=30Ω,电感L=12m H。求电路中电流及各元件两端电压的瞬时表达式,并作出相量图。

解:由给出条件,首先建立相量模型,如图2-14(a)所示。(www.xing528.com)

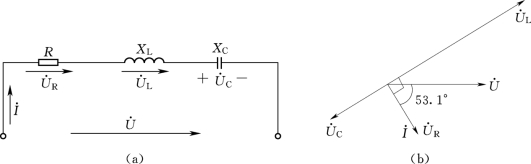
图2-14　[例2-8]的电路图

(1)已知

(2)复阻抗Z=R+j(XL-XC)=30+j(60-20)=30+j40=50∠53.1°(Ω)

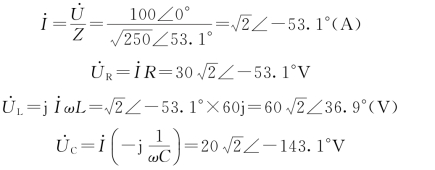
(3)

i=2sin(5000t-53.1°)A

uR=60sin(5000t-53.1°)V

uL=120sin(5000t+36.9°)V

uC=40sin(5000t-143.1°)V

从计算结果可以知道

U≠UL+UR+UC

(4)作出相量图,如图2-14(b)所示。

【例2-9】 电路如图2-15所示,已知,U1=100,试求:

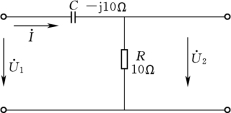
图2-15　[例2-9]的电路图

(1)电压u1与i之间的相位差。

(2)电路的有功功率、无功功率、视在功率。

(3)若u1的频率升高时,输出电压u2与u1之间的相位差是增大还是减少?

解:(1) Z=R-j-45°(Ω)

即u1与i之间的相位差为-45°,也就是说电路为电容性电路,电压滞后于电流45°。

(2)由于

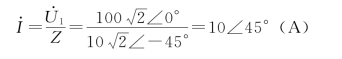
所以

或

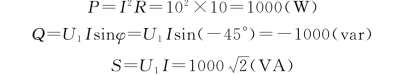
(3)当u1的频率升高时,电压与电流之间的相位差为

ω增大时,φ角减小,而电阻元件上电压u2与电流i同相,所以当u1频率升高时,u1与u2之间的相位差要减小。