电容电路：电压与电流的同频正弦关系

1.电压与电流的关系

线性电容元件在如图2-9(a)所示的联正方向的条件下

图2-9　交流电容电路

假定u=Umsinωt,则

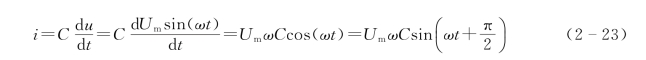
上式说明,电容两端加上正弦交流电压后,电容中的电流也是同频率的正弦量,但在相位上超前于电压90°,或者说电压落后于电流90°,对应的电压、电流波形见图2-9(b)。

根据式(2-23)令

Im=UmωC

或

I=UωC

令XC=,则

XC称为容抗,它反比于通过电容元件的电流的频率和电容元件的电容量。当ω的单位用弧度/秒(rad/s),电容C的单位用法拉(F)(简称法)时,XC的单位用欧姆(Ω)。

当电容元件加上直流电压时(ω=0)时,电容电流恒为零,相当于开路元件,也就是说电容元件有隔断直流电的作用。当电容元件被施加一定频率的交流电压时,由于电压的变化,电容极板上的电荷也发生增减,电荷的增减使得电容中有交变的电流流过,ω越高,电容极板上的电荷变化也就越快,电流也就越大,当ω趋于∞时,电容元件可用短路元件来替代。

据此可得出关于电容元件电压与电流关系的一般结论:

(1)电容元件两端的电压及流过电容中的电流均为同频率的正弦量。

(2)电容元件上电压滞后于电流90°的相位角。

(3)电压与电流的有效值关系为

电容元件上电压电流关系的相量形式为

或

相量图如图2-9(c)所示。

式(2-25)中(-j XC)可以看作电容参数的复数形式。

2.功率关系

电容元件交流电路的瞬时功率为

(www.xing528.com)

可见电容元件中的瞬时功率是幅值为UI、以2ω为角频率随时间而变化的交变量。这是因为电容是一个储能元件,当电容电压增高时,电容中的电场能量(WC=Cu2)将增加;它将从电源获取电能,则p＞0;当电容电压降低时,电容中电场能量减小,而将剩余的能量送回给电源,则p＜0。其能量变化的波形见图2-9(b)。

电容元件在交流电路中的平均功率为

与电感元件一样,电容元件也不消耗任何能量,在电容元件与电源之间只有能量变换,其互换的规模与电感电路一样,用无功功率Q来表示,该值等于瞬时功率的幅值,即

【例2-7】 一只容量为15μF电容器,将其接在有效值为220V、50 Hz的正弦电压上,试求:

(1)电容中流过的电流和无功功率;

(2)当电源电压不变,将频率变为1000 Hz时,重求电容中的电流。

解:(1)XC==212(Ω)

以电压为参考相量,则

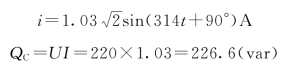
(2)f=1000 Hz

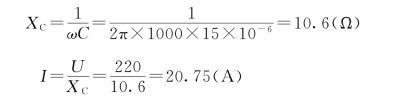
所以

可见,当电压一定时,频率升高,容抗就变小,电流增大。

为了同电感元件电路的无功功率相比较,同样设通入电容元件的电流为

i=Imsinωt

则

u=Umsin(ωt-90°)

于是得出瞬时功率

p=pC=ui=-UI sin2(ωt)

由此可见,电容元件电路的无功功率为

即电容性无功功率取负值,而电感性无功功率取正值,以资区别。

电阻、电容、电感在正弦交流电流电路中的作用和性质见表2-1。

表2-1　R、L和C元件在正弦交流电路中的作用和性质