电感电路中的电感元件特性

1.电压与电流的关系

图2-8所示的电路中,线性电感元件中的自感电动势为

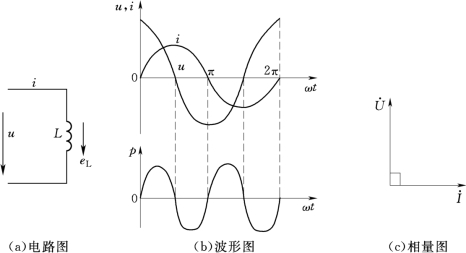
图2-8　交流电感电路

设流入的交流电流为

i=Imsinωt

根据KVL得

式(2-17)说明,电感电压也是正弦量,且与电流同频率,但在相位上电压超前于电流90°,在大小关系上

Um=ImωL,U=IωL

由上式可知,当ω一定时,电感两端的电压有效值正比于电流。当ω=0时,电感电压恒为零,即电感元件在直流电路中相当于短路。当ω趋于∞时,电感元件的作用相当于开路元件。

由上述讨论,可得出关于电感元件的一般结论:

(1)电感元件中的电压和电流均为同频率的正弦量。

(2)电感元件的电压超前于电流90°,波形见图2-8(b)。

(3)电压与电流的有效值关系为

令

则

从上式可知,电压一定时,XL越大,电流越小。可见XL具有阻碍电流的性质,所以称XL为电感电抗,简称感抗。

当ω的单位用弧度/秒(rad/s),L的单位用亨利(H)(简称亨)时,XL的单位为欧姆(Ω)(简称欧)。

感抗XL与电感L、频率f成正比,这是因为线圈的电感越大,或通过线圈的电流频率越高,则线圈中的自感电动势也就越大。由于自感电动势对电流起阻碍作用,该作用通过XL来体现。

若用相量形式来表示,则

(https://www.xing528.com)

或

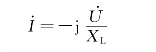
电感电路的相量图见图2-8(c),或式(2-20)中的j XL可视为电感参数的复数形式,该式说明了电压电流的有效值之比等于感抗,同时也说明了电压超前于电流90°的相位关系。

需要注意的是:≠XL,因为u与i的瞬时值关系并非线性关系,而是导数关系。

并非同相,而电压超前于电流90°。

2.功率关系

电感交流电路中的瞬时功率关系为

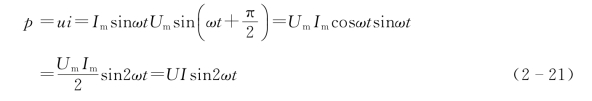
可见,电感电路中的瞬时功率是幅值为UI的2倍于电流、电压频率的正弦函数,其波形见图2-8(b)。电感电路中的瞬时功率正负交替变化的原因是电感线圈是一个储能元件,当电流增加时,线圈中磁场能量增加(磁场能量的表达式为W1=Li2),它从电源取用能量,其功率为正。当电流减小时,线圈中磁场能量也减小,由于电路中没有耗能元件,磁场释放的能量全部回送给电源,故p为负。也就是说虽然电路中有电压,也有电流,但从一周的整体效果上来看,它既不消耗电能,也不输出电能。这一点可以从平均功率得到验证。

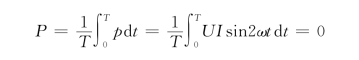
上式说明,在电感元件的交流电路中,没有任何能量消耗,只有电源与电感元件之间的能量交换,其能量交换的规模用无功功率Q来衡量,它的大小等于瞬时功率的幅值,即

无功功率的计量单位为乏(var)或千乏(kvar)。

需要注意的是,无功功率并非无用功率,例如后面我们要讨论的变压器、交流电机等电气设备需要依靠磁场传递能量,而其中电感性负载与电源之间的能量互换规模就得用无功功率来描述。

【例2-6】 今有一电感量L=0.1 H的线圈,线圈电阻甚小,可以忽略不计。现将其接在220V、50 Hz的正弦交流电源上,试求:

(1)通过线圈中的电流和无功功率;

(2)若电源电压不变,将频率变成1000 Hz,重新计算线圈中的电流。

解:(1)XL=ωL=2πf L=2π×50×0.1=31.4(Ω)

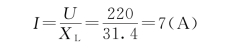
设电源电压为参考相量,且电压电流为关联正方向,则

则

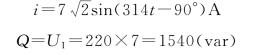
(2)当f=1000 Hz时,则

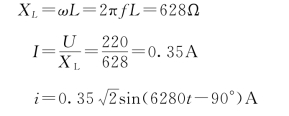
可见同一个电感线圈,对低频限流作用较小,而对高频限流作用较大。