正弦量的相量表示及其物理意义

在分析线性电路时,正弦激励和响应均为同频率的正弦量,频率是已知的,可不必考虑。因此,一个正弦量由幅值(或有效值)和初相位就可确定。一个复数由模和辐角两个特征来确定。因此正弦量与复数之间存在着一一对应的映射关系,则正弦量可以用复数来表示,正弦量的运算可以借助复数的运算进行。为了与一般的复数区别,我们把表示正弦量的复数称为相量。复数的模对应正弦量的幅值或有效值,复数的辐角对应正弦量的初相位。把以正弦量的幅值为模的复数称为最大值相量,如把以正弦量有效值为模的复数称为有效值相量,简称相量,如显然,最大值相量等于有效值相量乘以一般所说的相量即指有效值相量。

正弦量的相量书写规定为:在大写字母上打“·”。于是表示正弦电压u=Umsin(ωt+ψ)的相量式为

注意,相量只是表示正弦量,而不是等于正弦量。正弦量是时间的实函数,具有明确的物理意义,相量则是一种复数形式。正弦量的相量形式仅是分析交流电路中各电量关系的一种符号。在进行正弦量运算时,首先应把正弦量用复数表示成相量,然后根据复数运算(相量运算)所得的相量结果,再对应的写出正弦量。

按照各个正弦量的大小和相位关系画出的若干个相量的图形,称为相量图。我们规定:相量与实轴的正方向之间的夹角为初相角,该相量逆时针旋转时夹角为正,顺时针旋转时夹角为负。在相量图上能形象地看出各个正弦量的大小和相互间的相位关系。

只有正弦周期量才能用相量表示,相量不能表示非正弦周期量。只有同频率的正弦量才能画在同一相量图上,不同频率的正弦量不能画在一个相量图上,否则就无法比较和计算。

由上可知,表示正弦量的相量有两种形式:相量图和复数式(相量式)。

【例2-3】 已知i1=10sin(314t-30°)A,i2=-8sin(314t+60°)A,i3=5cos(314t+30°)A,试用相量表示法表示各正弦电流,并作相量图2-6。

解:首先将瞬时值表达式化成标准形式:

i2=-8sin(314t+60°)=8sin(314t-120°)A

i3=5cos(314t+30°)=5sin(314t+120°)A(www.xing528.com)

则

【例2-4】 已知u1=311sin314t V,u2=100(314t+60°)V,试用相量法求两正弦量之和。

解:

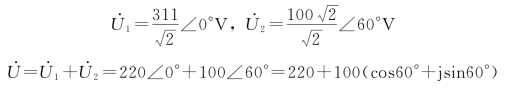
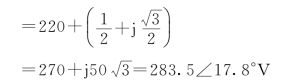
则

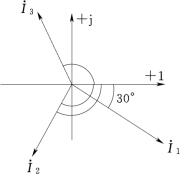
图2-6　[例2-3]相量图