节点电压法——解决电路问题的基本方法

以节点电压为未知量,列写KCL方程,然后求解电路的方法称为节点电压法。其步骤如下:

(1)在电路中任选一节点作为参考点,参考点电位为零。

(2)应用KCL列出其余(n-1)个节点电流方程。

(3)用KVL和欧姆定律列出节点电压与支路电流的关系式,并将其代入节点电流方程,得出(n-1)个节点电压方程。

(4)联立求解方程组,得各节点电压。

(5)利用节点电压与支路电流的关系式,求出各支路电流及其他待求量。

【例1-8】 如图1-24所示电路,已知E1=12V,E2=-12V,R1=2kΩ,R2=4kΩ,R3=1kΩ,R4=4kΩ,R5=2kΩ,用节点电压法求各支路电流。

解:先选定d点作为参考节点,设Vd=0。根据各支路电流正方向就节点a、b列出电流方程。

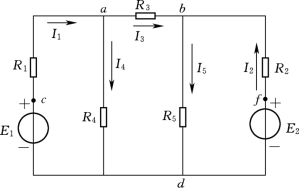
图1-24　[例1-8]的电路图

节点a

节点b

由图1-24可知,Vc=E1,Vf=E2,所以

将各电流值代入式(1-14)和式(1-15)中,整理得

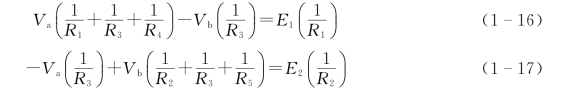
将数值代入式(1-16)和式(1-17)中,可求出a、b两节点的电压为

Va=3.64V,Vb=0.363V

求出a、b两节点的电压后,利用节点电压与支路电流的关系可求出各支路电流为(www.xing528.com)

I1=4.18m A,I2=-3.09m A,I3=3.28m A,I4=0.91m A,I5=0.183m A

节点电压法特别适用于分析节点数少而支路数较多的电路。如图1-23所示,选b点为参考点,设Vb=0,对节点a列出KCL方程

I1+I2-I3=0

各支路电流与节点电压的关系为

将各电流代入电流方程并解得

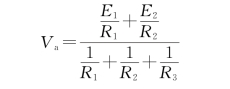
将上述结论加以归纳,可以得到任意两节点网络的节点电压表达式为

上式所示关系亦称为弥尔曼定理,仅适用于节点数的电路。式中分母各项是所有支路总电阻的倒数之和,符号为正号;分子各项为含源支路的电源电流,其符号取决于该支路电源的极性。恒压源的电动势指向待求节点时符号为正,相反为负;恒流源的电流指向待求节点时符号为正,相反为负。

【例1-9】 用节点电压法重解[例1-7]。

解:

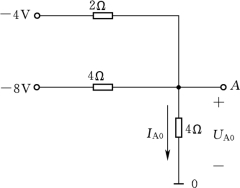
图1-25　[例1-10]的电路图

【例1-10】 用节点电压法计算图1-25中的电压UA0和电流IA0。

解:该电路只有两个节点:A和0。UA0即为节点电压或A点的电位VA。