6.4.2有负载的变幅杆

以上几节所讨论的变幅杆特性都是在其处于空载的形式下进行的，即变幅杆处在两端自由状态，而在实际应用中，变幅杆不可能没有负载。当变幅杆有负载时，其共振频率将发生变化，如果要保持共振频率不变，则要适当改变变幅杆的长度。

变幅杆的负载随应用场合的不同差别很大，而且在工作过程中负载始终是在变化的。在变幅杆末端负载呈现为机械阻抗。这里仅讨论单一变幅杆有阻抗负载时的特性。

6.4.2.1 负载阻抗对变幅杆共振频率的影响

由纵波振动的波动方程及边界条件可推导出变幅杆有负载阻抗X_L时的频率方程，见表6.4-5。

表6.4-5 几种变幅杆形式有负载力抗X_L时的频率方程

6.4.2.2 简单形状加工工具头对变幅杆共振频率的影响

在超声加工应用中，变幅杆的末端需要连接不同形状的工具，用以对材料或零件进行加工处理。若工具为均匀截面杆，并且其横向尺寸<λ/10，长度<λ/4，则可以用式（6.4-2）来计算工具头的等效质量M_t

式中，m_t=S_tltρ_t（工具质量）；S_t为工具截面积；l_t为工具长度；ρ_t为工具材料密度；k_t=ω/c_t；c_t为工具材料的纵波速度。

1.有工具头的圆锥形变幅杆

共振频率为

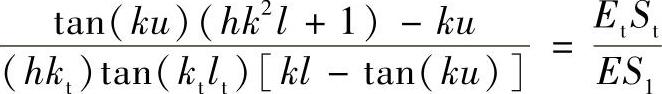
式中，u=（l-h）；E_t为工具弹性模量；h为圆锥顶点到变幅杆小端面的距离。

2.有工具头的指数形变幅杆

共振频率为

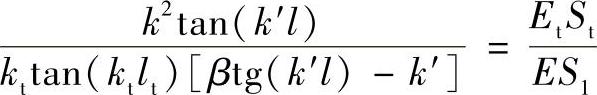
3.有工具头的阶梯形变幅杆

共振频率为

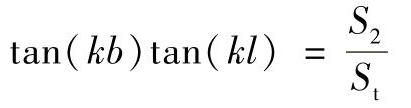
4.计算举例

1）已知条件。圆锥形变幅杆所用材料为45钢，c=5.17×10⁶mm/s，大端直径D₁=15mm，小端直径D₂=5mm，工作频率为20kHz，小端上附加工具头直径为2mm，长为10mm，求变幅杆长度。

2）应用公式。有工具头的圆锥形变幅杆的共振长度公式为：(www.xing528.com)

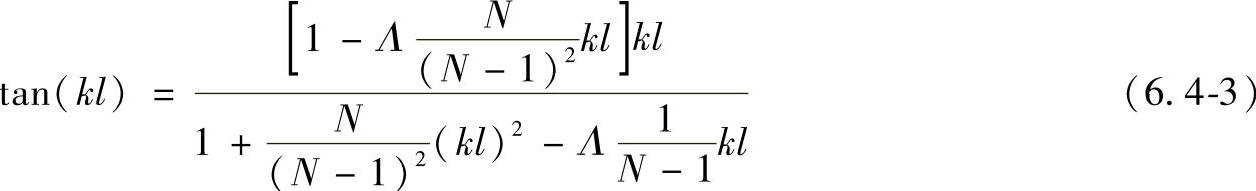
式中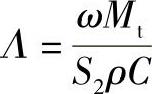，，一般取Λ＜0.25，S₂为变幅杆小端面积；ρ为变幅杆材料密度；c为变幅杆材料中的声速。

为了便于计算，将式6.4-3中kl与N、Λ关系数据列于表6.4-6。

表6.4 - 6 有工具头圆锥形变幅杆中kl与N、Λ的关系

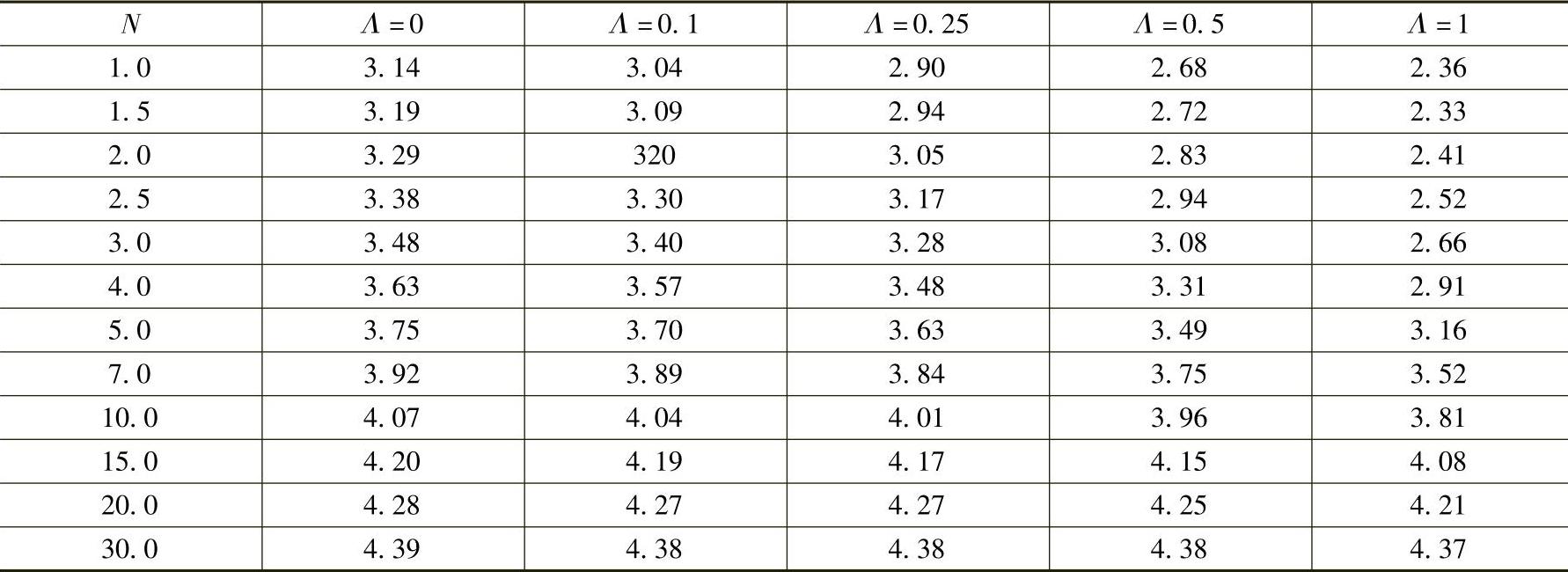
3）计算方法。工具质量

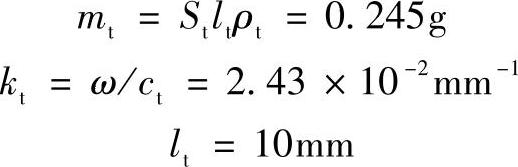
所以

Tan（k_tl_t）=0.248

带入式（6.4-2）得

M_t =0.250g

由Λ定义式得

Λ=3.99×10^-2

因为

N=D₁/D₂ =3

所以，由式（6.4-3）可得

kl=3.45

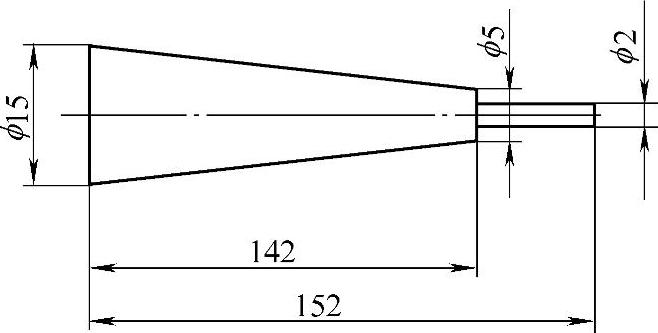
图6.4-8 工具头的圆锥形变幅杆

k=2.34×10^-2mm^-1

l=142mm

由此可得，有工具头的圆锥形变幅杆的几何尺寸如图6.4-8所示。