6.4.1.1 变截面杆纵振动的波动方程
物体在弹性介质中发生振动时会引起介质的振动,在研究振动波时对于所有固体都可以看作是弹性体。由于介质各点之间存在着弹性的联系,一点振动时相邻各点将被带动依次振动起来。这样,物体的振动就在弹性介质中传播出去。这种物体的振动在弹性介质中的传播被称为波动。以质点和简单机械振动系统的振动及超声波的传播原理为理论基础,建立数学模型,根据牛顿定理确定变截面杆纵振动的波动方程。
为了研究方便,设定理想状态,即假定变截面杆是由均匀、各向同性材料所构成的,略去机械损耗。当杆的横截面尺寸远小于波长时,可以认定平面纵波沿杆轴向传播,在杆的横截面上应力分布是均匀的。
如图6.4-1所示,任一变截面杆,其对称轴为x轴,任选一小体积元(x,x+dx所限定的区间)作用其上的张应力为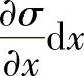 ,根据牛顿定律可以得出动力学方程
,根据牛顿定律可以得出动力学方程
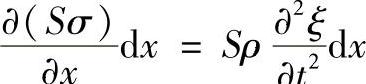
式中,S为杆的横截面积函数,S=S(x);ξ为质点位移函数,ξ=ξ(x);σ为应力函数,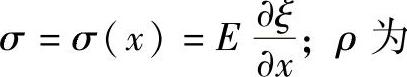 杆材料的密度;E为弹性模量。
杆材料的密度;E为弹性模量。
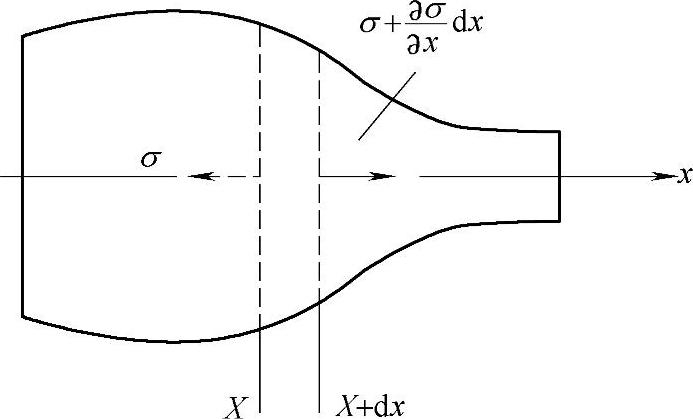
图6.4-1 变截面杆的纵振动
在谐振条件下,可以得出变截面杆纵振动的波动方程

式中,k为圆波数,k=ω/c;ω为圆频率;c为纵波在细棒中的传播速度,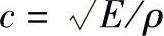 。
。
我们将以波动方程式(6.4-1)作为基础来讨论单一变幅杆和复合变幅杆的参数计算及形状设计。
6.4.1.2 单一变幅杆
1.单一变幅杆的特性参数
超声变幅杆的性能主要是由变幅杆的共振长度l、放大系数Mp、形状因数φ、位移节点x0、输入力阻抗Zi和弯曲劲度等参数加以描述的。其中放大系数Mp是指变幅杆工作在共振频率时,输出端与输入端的质点位移或速度的比值。形状因数φ是衡量变幅杆所能达到最大振动速度的指标之一,它仅与变幅杆的几何形状有关,φ值越大,通过变幅杆所能达到的最大振动速度也越大。如等截面杆的φ值为1,常用变幅杆的φ值都接近于3,而某些特殊形状的变幅杆,φ值可达5左右。输入力阻抗Zi定义为输入端策动力与质点振动速度的复数比值。在实际应用中常常要求输入力阻抗随频率及负荷的变化而变化的幅度要小。弯曲劲度是弯曲柔顺性的倒数,弯曲劲度也与变幅杆的几何形状有关。变幅杆越长,弯曲柔顺性越大,在许多实际应用中这是需要避免的。
上述变幅杆各性能参数是根据纵振动波动方程和杆的面积函数及边界条件推导出的公式来确定的。其中,边界条件如图6.4-2所示。设坐标原点x=0处的横截面积为S1,x=l处的横截面积为S2。作用在S1、S2上的力及振动速度分别为F1、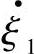 和F2、
和F2、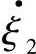 。则边界条件如下:
。则边界条件如下:
1)两端自由时
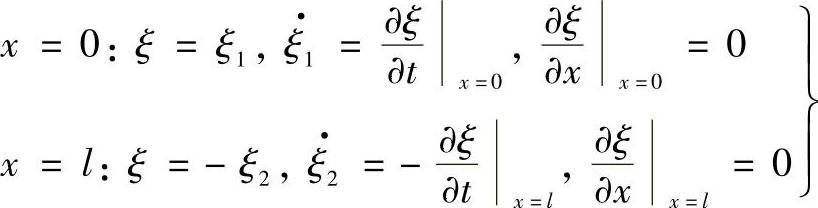
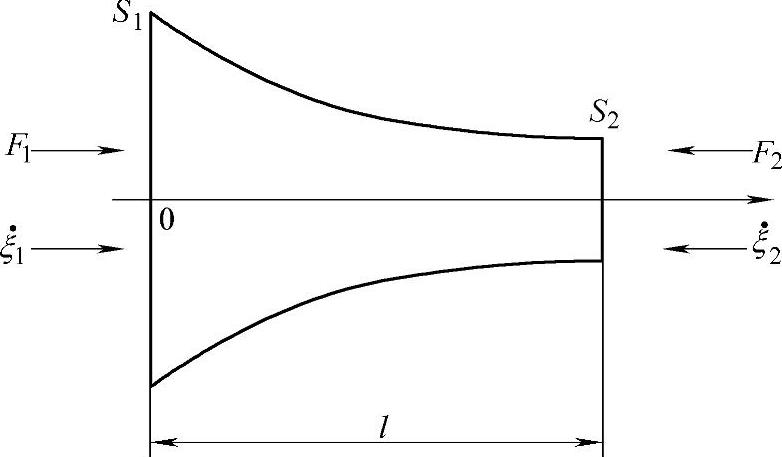
图6.4-2 变截面杆
2)一般情况时
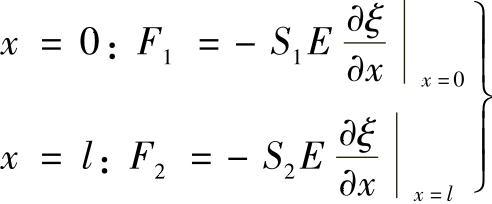
表6.4-1列出了指数形、圆锥形、悬链线形、阶梯形等四种圆截面半波长谐振变幅杆的设计公式,用于对谐振频率、半波谐振长度lp、位移节点长度x0、放大系数Mp、应变极大点长度xM和形状因数φ等参数的计算。另一个重要参数输入力阻抗Zi由表6.4-2列出。
表6.4 - 1 四种半波谐振变幅杆设计计算公式和方程
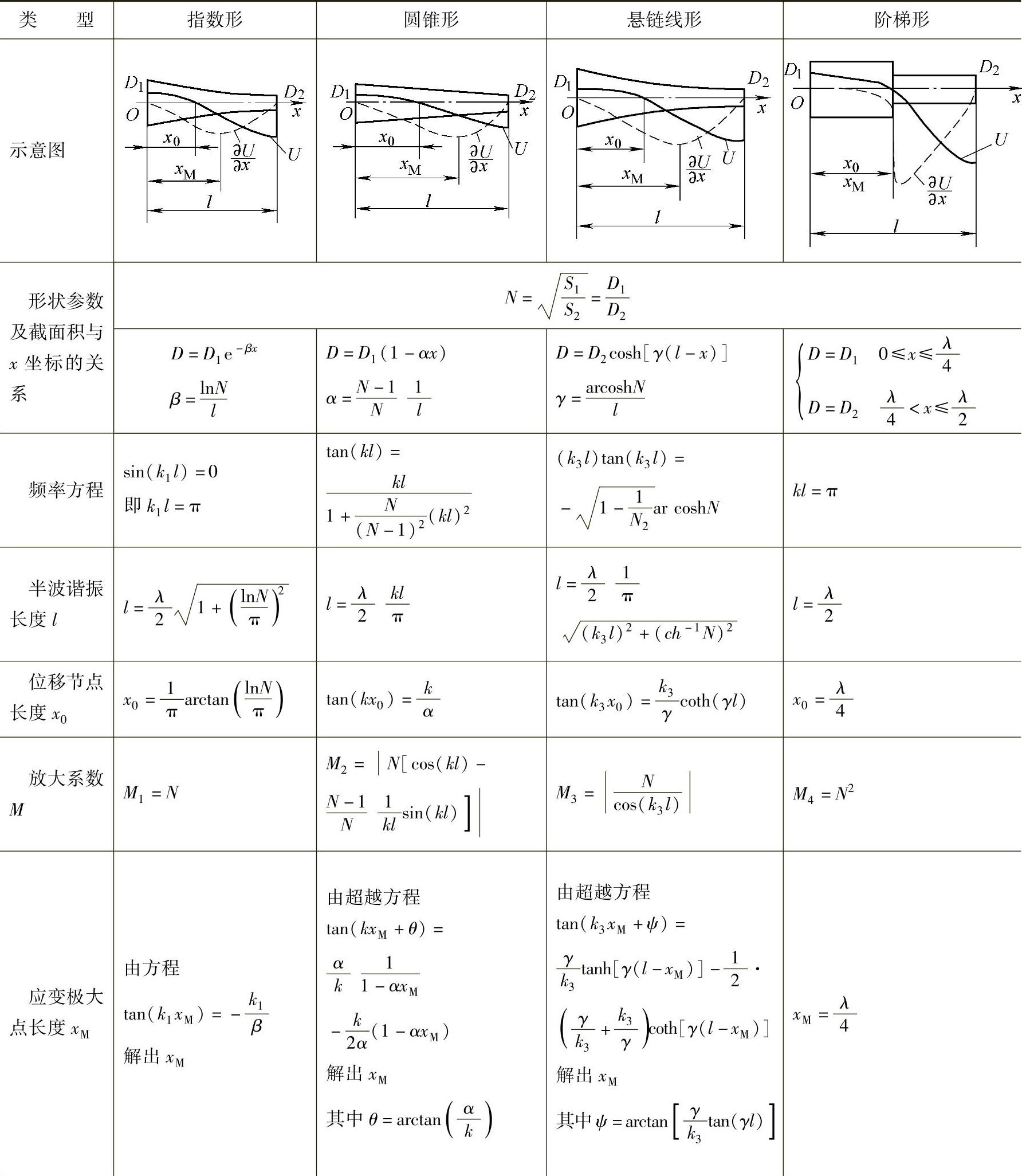
(续)

表6.4 - 2 输入阻抗方式

2.四分之一波长变幅杆
四分之一波长变幅杆在设计复合变幅杆或组合换能器时是经常用到的。质点位移节点的设定有两个特定的位置,分别处于变截面杆的大端或小端。
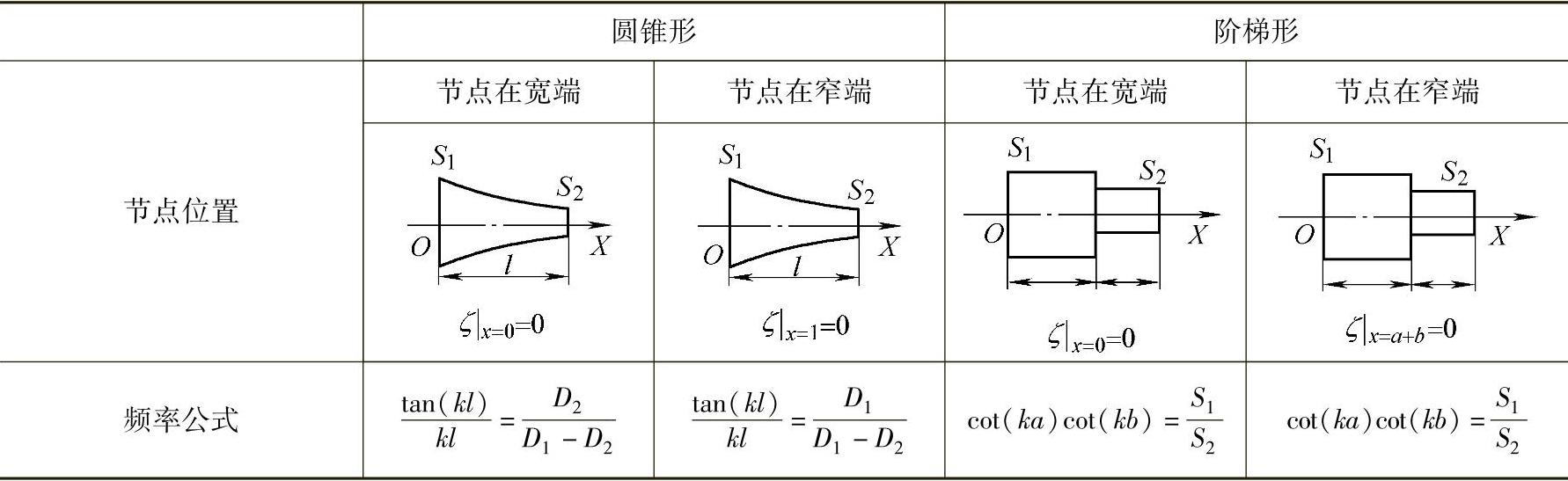
当四分之一波长变幅杆的一端处于波节时,该端振动位移或速度为零,如果在理想状态下,对于无损耗的四分之一波长变幅杆就其两端振幅比而言,其放大系数Mp为无限大,处于节点一端的输入阻抗Zi也是无限大的。在实际应用中材料是有损耗的,并且杆的另一端也是有负载的,因此Mp及Zi都是有限值。但由于四分之一波长变幅杆具有Mp及Zi数值都较大的特点,故在换能器设计中常用其作为阻抗匹配组合,以提高换能器的辐射效率。表6.4-3给出了其频率设计公式,在确定大、小端面积和频率后可利用这些公式计算出杆的长度。
表6.4 - 3 四分之一波长变幅杆频率设计公式
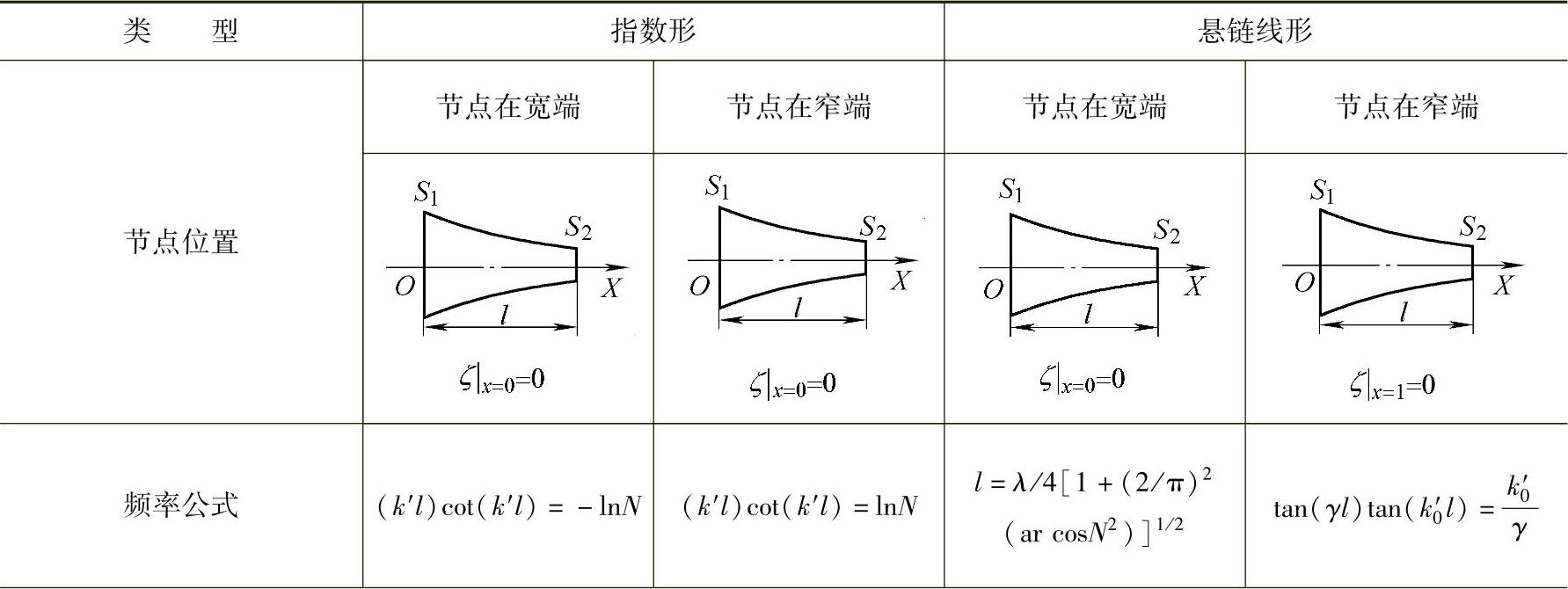
(续)
6.4.1.3 复合变幅杆
在高强度超声应用中,常常要求变幅杆末端具有很大的振动幅度,这就要求变幅杆的形状因数φ及放大系数Mp值都尽可能的大,上一节介绍的几种单一变幅杆的φ值和Mp值常出现此优彼劣的现象,很难二者兼顾。为了改变这一状况,就必须采用复合变幅杆的形式来弥补不足,以提高其输出性能。在有些应用场合需要特别高的振动速度时,也常用到长度满足共振条件的复合形变幅杆。(https://www.xing528.com)
图6.4-3所示为三段复合变幅杆。其中Ⅰ和Ⅲ段为等截面杆,Ⅱ段为变截面杆,而变截面杆可以是指数形、圆锥形或悬链线形等不同形式。如果两等截面杆的长度相等,则构成具有变截面过渡段的阶梯形变幅杆。当Ⅰ或Ⅲ的任一段为零,则可构成两段复合变幅杆。
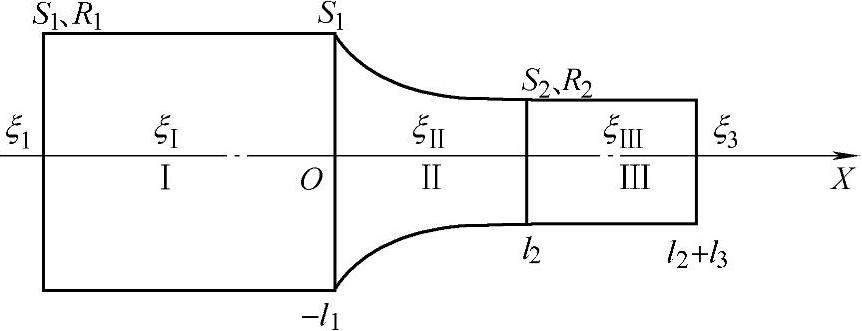
图6.4-3 复合变幅杆
讨论复合变幅杆与单一变幅杆的方法大体相同,从变截面的波动方程式(6.4-1)出发,推出各段杆中的振动位移,并将其输入力阻抗、频率方程、放大系数和形状因数等参数的公式即可。下面介绍几种复合变幅杆。
1.一端带有圆柱杆的复合变幅杆
表6.4 - 4 两种复合变幅杆的设计公式
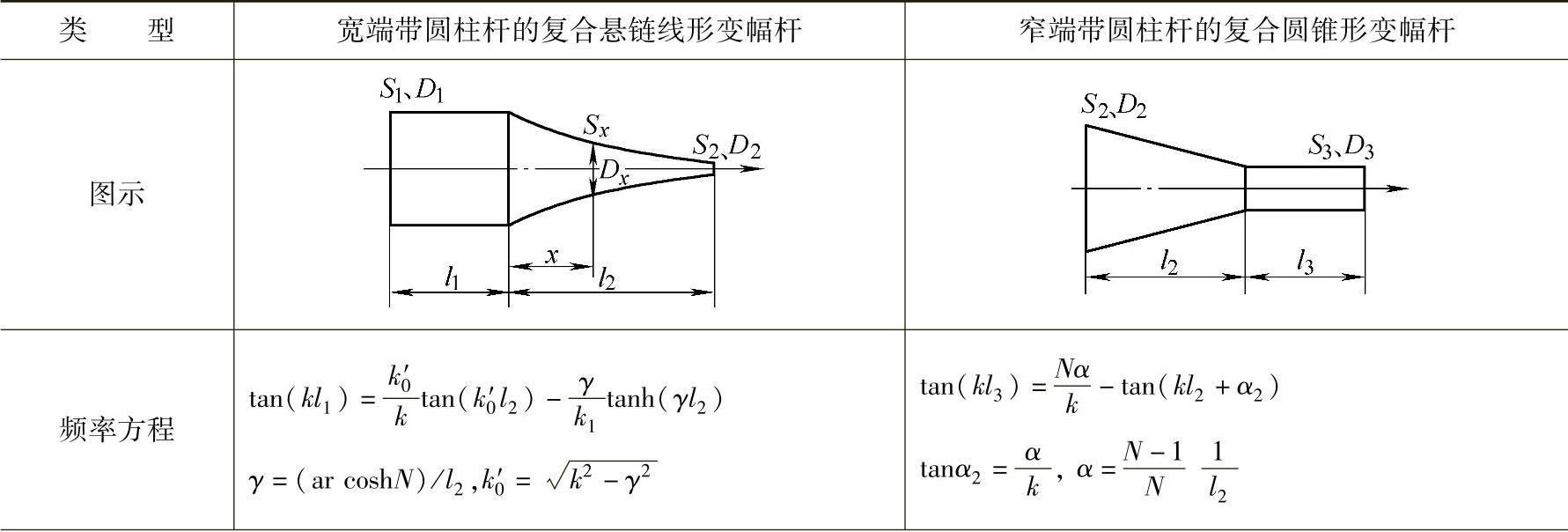
一端带有圆柱杆的复合变幅杆比较常用的有两种:其一是大端接圆柱杆的复合悬链线形变幅杆,其二是小端接圆柱杆的复合圆锥形变幅杆,这两种变幅杆的优点是放大系数Mp比较大。表6.4-4列出了这两种复合变幅杆的设计公式。图6.4-4、图6.4-5所示分别为这两种复合变幅杆(kl3=0,或kl1=0)各性能参数与kl2的关系曲线(N=3)。由曲线图中可以看出形状因数φ与相对放大系数Mp/N存在最大值,即在确定N值的条件下有一确定的kl2值可使φ及Mp达到最大值。
(续)

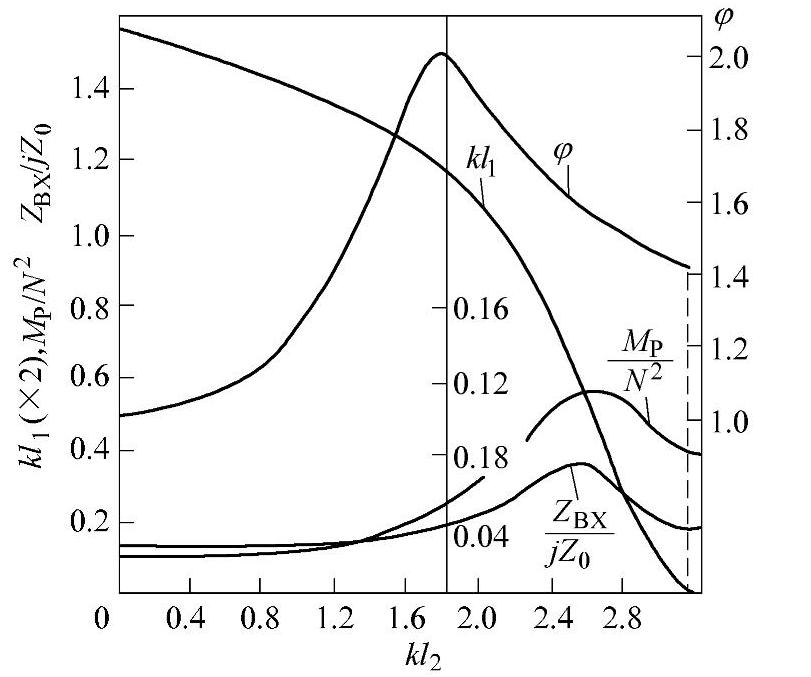
图6.4-4 大端接圆柱杆的复合悬链线形变幅杆各参量与kl2的关系曲线(kl3=0)
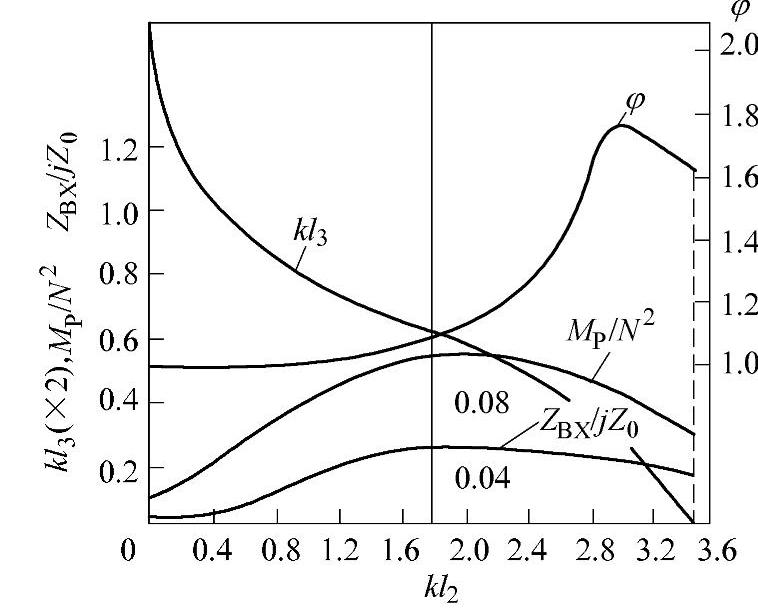
图6.4-5 小端接圆柱杆的圆锥形变幅杆各参量与kl2的关系曲线(kl1=0)
2.倒锥形复合变幅杆
当换能器向液体介质辐射声波时,为了提高辐射声能,常采用倒锥形复合变幅杆加大辐射面积,用以改善换能器与辐射介质之间的阻抗匹配。图6.4-6所示为由四分之一波长的圆柱杆和圆锥体组合而成的半波共振倒锥形复合变幅杆。
1)共振条件为
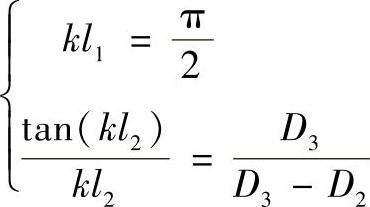
2)放大系数Mp为
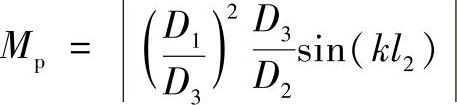
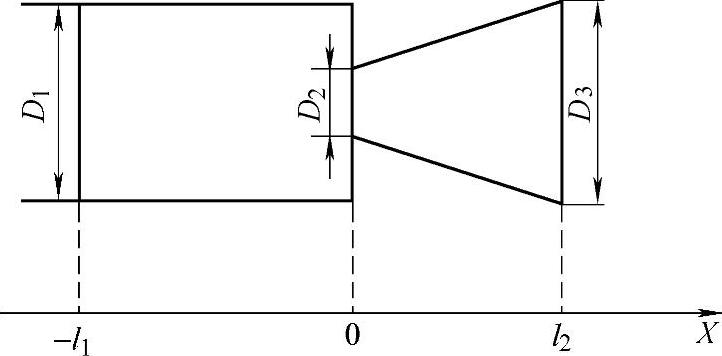
图6.4-6 倒锥形复合变幅杆
3)位移节点x0为
x0在坐标x=0处。
4)输入力阻抗Zi
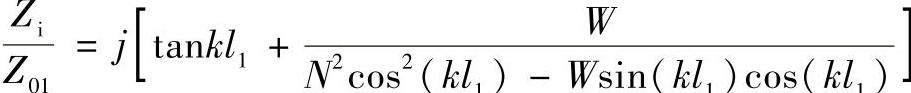
式中,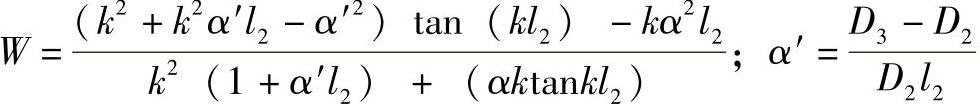
3.高斯形变幅杆
以高斯曲线为外形的变幅杆具有输出端可达到很高的振动速度,而变幅杆本身不受材料疲劳强度限制的特性。在实际应用中,只取高斯曲线中的一段作为变幅杆的中段,输出、输入端必须由具有一定截面的部分组成。图6.4-7所示为一个实例。图中高斯曲线段Ⅱ与均匀杆Ⅲ组成λ/4,而另一λ/4段I为圆柱段也可以是阶梯杆或悬链线形杆,共同组成半波长谐振的复合高斯形变幅杆。
图6.4-7b所示为其应力沿轴向x的分布曲线,在高斯曲线段应力分布均匀。λ/4复合高斯杆的谐振长度为:
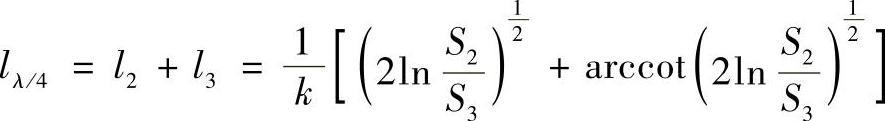
式中,k=ω/c,c为细杆材料中的纵波速度。
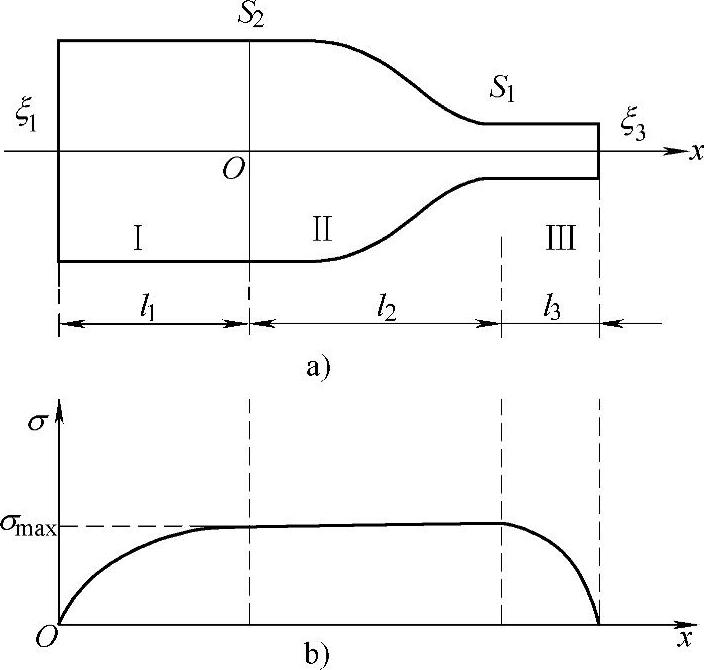
图6.4-7 复合高斯形变幅杆及其应力分布
a)变幅杆 b)应力分布
放大系数为
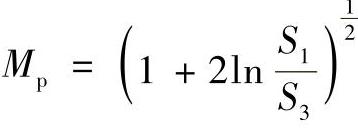
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




