磁致伸缩换能器的工作原理及应用

6.3.1.1 磁致伸缩材料的特性及换能器的工作原理

1.磁致伸缩材料的特性

（1）纵向磁致伸缩正效应（焦耳效应）铁磁材料（如铁、镍、钴及其合金等）制成的棒在受外磁场作用时，沿磁力线方向会产生伸缩相对形变的效应称为纵向磁致伸缩正效应（或称焦耳效应）。

纵向磁致伸缩效应具有下面一些性质：

1）纵向磁致伸缩效应所引起的相对形变是较小的，约在10^-6数量级。

2）不同铁磁材料制成的棒，在相同磁场强度或磁感应强度作用下所产生的相对形变是不同的。如图6.3-1所示。从中可以看出，45%坡莫合金的相对形变总是正的，纯镍、退火钴的相对形变总是负的，而纯铁在弱磁场时是正的，在强磁场时变为负的。

3）磁致伸缩形变与温度有密切关系，当温度升高时，由于铁磁材料晶格的变化，磁化强度会发生变化，变化的情况如图6.3-2所示。从中可看出，几条变化的曲线形态各异，但无论是哪种变化情况，它们都存在一个Q_T的温度，一旦到达这一温度，自发磁化不再存在，铁磁体变为顺磁体。我们称Q_T为居里点。要使磁致伸缩换能器正常工作，必须让它处于远低于居里点的温度环境内，在设计大功率辐射器时尤其要考虑温度对换能器的影响问题。

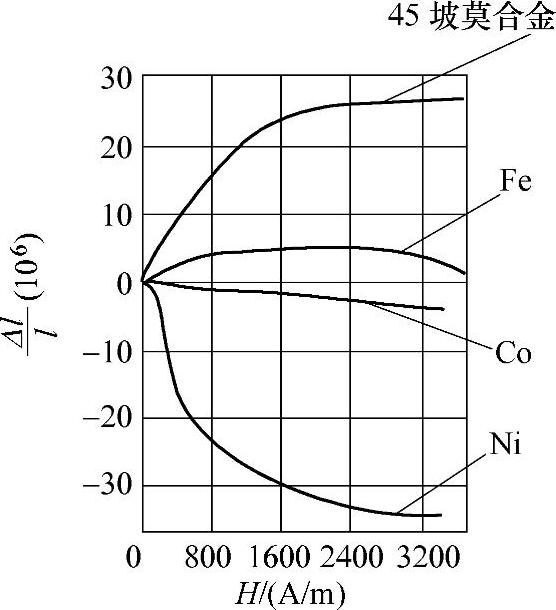
图6.3-1 （Δl/l）与磁场强度H的关系

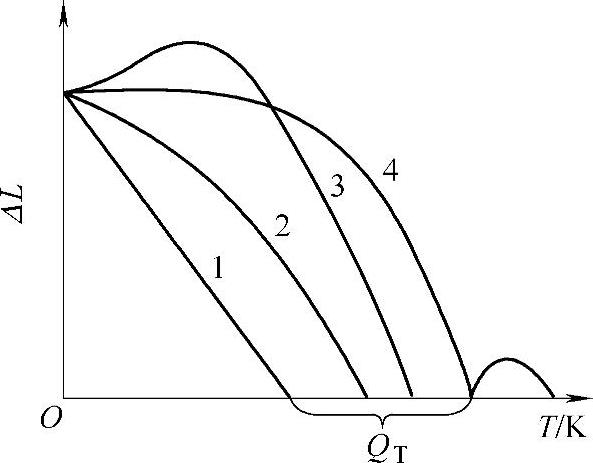
图6.3-2 磁致伸缩形变随温度变化

4）磁致伸缩材料均具有磁致伸缩饱和现象，当外加磁场强度逐渐增大时，开始时形变会随之逐渐增加，当磁场强度增加到某一值时，形变就不再增加，此时的形变称为饱和磁致伸缩形变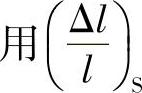，来表示。例如，退火镍在磁场强度为4800A/m时饱和磁致伸缩形变为-36×10^-6。

5）相对形变近似与磁感应强度B的平方成正比。

式中，k（B）为比例系数。

由于相对形变与磁感应强度是偶函数关系，所以在交变磁场作用下，应变或应力会出现倍频效应，换能器辐射的超声波频率将为交变磁场的两倍。人们往往不希望出现这种情况。为了实现换能器同频的机电能量转换，需另加一个恒定的极化磁场，使换能器系统处于极化状态，当另有较小的交变磁场作用时，就可以得到同频的机电能量转换了。对于这种极化系统，磁感应强度是由恒定的B₀和交变的B两部分组成的，在B为谐和变化时，磁致伸缩应力由恒定力、同频力和倍频力所组成，在倍频力远小于同频力时，同频力就作为磁致伸缩应力，它与磁感应强度的关系如下：

T=σ（B₀）B

式中，σ（B₀）为磁致伸缩应力常数，它是极化磁感应强度的函数。

同一种材料，B₀不同σ（B₀）也会不同，要想得到最佳的磁致伸缩工作特性，除必须选择性能优异的磁致伸缩材料外，还需要选择优良的极化状态，即工作点，在该工作点上能得到最大的σ值。

（2）纵向磁致伸缩反效应（魏拉里效应） 对极化后的磁棒沿其长度方向施加外力时会产生相对形变，棒内的磁场强度会发生变化，这种效应叫纵向磁致伸缩反效应（或称魏拉里效应）。该效应可用下式表示：

式中，H～为内部产生的附加磁场强度；λ（B₀）为反向磁致伸缩常数，它是B₀的函数。

对于没有极化的磁棒，即使受外力作用发生形变，也不会产生磁场，换句话说，非极化的铁磁材料不存在反效应。

（3）涡流损耗 在铁磁物质中，当磁感应强度发生变化时，在其内部将产生感应电流，该感应电流所产生的磁场将阻碍磁感应强度的变化，阻碍铁磁材料的磁化，一部分能量被损耗掉变成热能，这种电流被称为涡流。涡流的存在导致动态磁导率的降低，且磁感应强度将会比磁场强度更滞后一个相位角φ₂。

磁致伸缩换能器主要在10～100kHz的频段内应用，在这个频段内，涡流损耗的影响不能忽略。涡流损耗与外加磁场的频率、铁磁材料的电阻率以及材料的形状有关。为了降低涡流损耗，磁致伸缩材料通常都做成薄片形。

考虑磁滞损耗和涡流损耗同时存在时，则材料的复磁导率可写成下面的形式：

式中，χ为涡流的去磁系数。

2.磁致伸缩换能器的工作原理

磁致伸缩换能器是由磁致伸缩材料制作的铁心外面缠绕线圈而成，如图6.3-3所示。当线圈中通以一定直流电流I₀产生最佳偏磁场H₀后，再通以交变电流I使其产生交变磁场H～，使H～重叠于H₀之上，由此铁心中的磁场将在H₀水平上变化。在交变磁场H～的作用下，由于材料的磁致伸缩效应（焦耳效应），换能器两端面产生与交流电频率相同的交变伸、缩，当交变电流的频率与换能器的共振频率一致时，换能器端部振动最强烈，由此从换能器两端面向介质辐射出超声波。

6.3.1.2 磁致伸缩换能器的材料

对用于磁致伸缩换能器材料的基本要求如下：

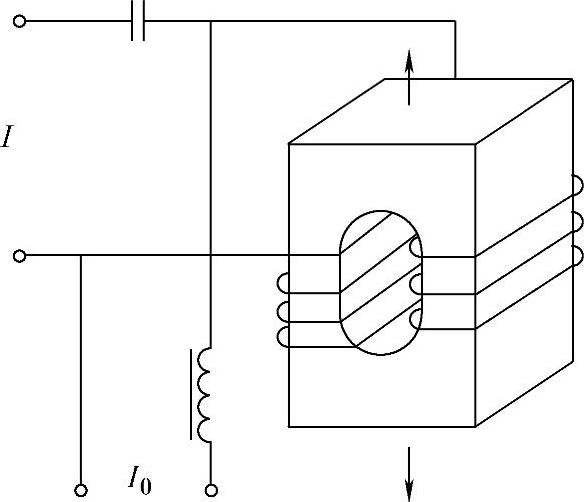
图6.3-3 磁致伸缩换能器

1）磁致伸缩应力常数要尽可能大。

2）磁滞及涡流损耗要尽可能小。

3）对高强度辐射换能器所用的材料，其饱和磁致伸缩值要大。

4）材料疲劳强度要高。

5）对于金属磁致伸缩材料，要易于轧制成薄片及加工成形。

常用磁致伸缩材料可分为两大类，一类是金属磁致伸缩材料，如镍、铁钴合金、铝铁合金等，另一类是铁氧体磁致伸缩材料。常用的铁氧体磁致伸缩材料有镍铜系和镍锌系铁氧体。

6.3.1.3 磁致伸缩换能器的结构形式和特点

1.窗式换能器

（1）结构形式 窗式磁致伸缩换能器是由薄片磁致伸缩金属材料（如镍、铁钴合金、铝铁合金等）经冲孔成形、氧化绝缘、叠集成块、退火等工艺制成的。由于它是由许多薄片叠集而成，叠片上有孔，形似窗孔，所以被称为窗式换能器。其基本结构形式如图6.3-4所示，图6.3-4b和图6.3-4c是双窗式和三窗式结构，它们可以分别看成是由图6.3-4a所示的两个或三个单窗式组成。

这种换能器的特点是从两端面辐射超声波。通常采用的叠片厚度为0.1～0.3mm。因为金属材料的电阻率低，因此片与片之间需要氧化绝缘，以减少涡流损耗。叠片上有孔，在叠片中形成闭合磁回路，漏磁少，并有利于散热。根据选用的叠片多少，可以获得不同的辐射面积。通常辐射面的形状为正方形。

图6.3-4 窗式磁致伸缩换能器

a）单窗式 b）双窗式 c）三窗式

单窗式换能器一般用于中、小功率（数十瓦到一千瓦左右）的超声设备上。双窗式和多窗式换能器，由于辐射面积增大，同时窗孔增多，改善了冷却条件，减少了横振动，输入电功率可以增加，可用于大功率超声设备上。

（2）换能器的共振频率公式及结构参数的选取 对于图6.3-5a所示的单窗式换能器，由于其形状的对称性，在计算共振频率时，通常只考虑组成换能器的一个侧肢（见图6.3-5b）即可。

在对称盖板情况下，分析带对称盖板的一根棒（见图6.3-5b）的波动方程式，在两端自由，中间作为位移节点的条件下，得到下面的共振方程式

tan（ka）tan（kb）=q（6.3-1）式中，a为盖板高度；2b为振动棒长度；q为面积系数，q=S₁/S₂=l₁/l₂；k为波数，k=ω/c；ω为圆频率，ω=2πf₀；f₀为换能器共振频率；c为换能器材料的声速。

根据参数a、b、q利用公式（6.3-1）求出k值，然后根据k=2πf₀/c求出f₀。也可以利用下面的公式直接计算出窗形磁致伸缩换能器共振频率f₀。

图6.3-5 单窗式换能器

换能器的结构参数取决于许多因素，可以按表6.3-1所列特点考虑选取。

表6.3 - 1 换能器结构参数选取特点

在工作频率给定，盖板高度a和面积系数q选定之后，利用公式（6.3-1）可以求出振动棒长度2b。

用公式（6.3-2）求出的换能器共振频率与实际测量值较为接近，其误差小于1.5%。这样的误差值对于超声设备设计来说并无大的影响。

窗式换能器在实际工作中应用较多，表6.3-2中列出了几种镍制窗式磁致伸缩换能器的工作频率和主要尺寸。

表6.3-2 几种镍制窗式磁致伸缩换能器

2.环形换能器

（1）结构形式 环形磁致伸缩换能器也是由薄片磁致伸缩金属材料，经冲孔成形、氧化绝缘、叠集成块、退火等工艺制成的，其结构形式如图6.3-6所示。

这种类型换能器的特点是：当线圈中同时通过偏磁电流和交变电流后，圆环受到磁致伸缩应力的作用，沿圆周产生长度伸缩的变化，因而产生径向振动，可以自圆环内侧面（见图6.3-6a）或外侧面（见图6.3-6b）向周围介质辐射超声波。

（2）换能器的共振频率公式及结构参数的选取 对于图6.3-7所示的作径向振动的环形换能器，如果圆环的半径R比圆环宽度a足够大，则其共振频率为

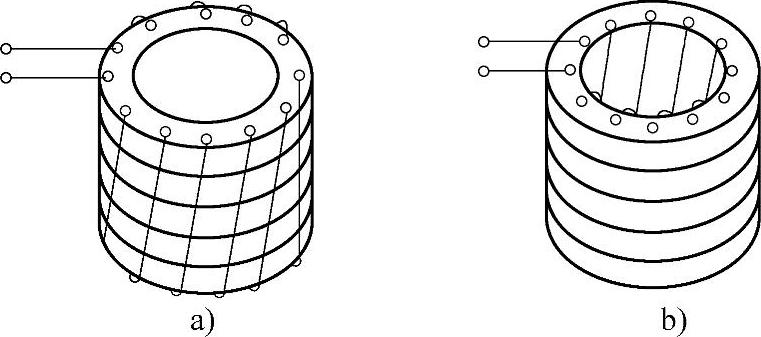
图6.3-6 环形磁致伸缩换能器

a）内侧面辐射 b）外侧面辐射

式中，E为弹性模量；R为圆环平均半径；ρ为材料密度；c为纵波声速。

在实际应用中，环形换能器叠片上均带有小孔，以便绕线。考虑到圆环上带有小孔后，可以将圆环看成是由两个同心圆环A和B组成，如图6.3-8所示。其共振频率可按下式计算：

式中，r₂及a₀´分别为4环的平均半径及A环的宽度；r₄及a₀分别为B环的平均半径及B环的宽度；n为B环上的小孔数；d为B环上的小孔直径。

图6.3-7 环形换能器

图6.3-8 环形换能器叠片

图6.3-9 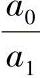与A的关系曲线

式中，。

与k的关系曲线如图6.3-9所示，a₁为B环有孔部位视为均匀棒时的等效宽度。

3.铁氧体换能器

(1)结构形式 铁氧体换能器是由磁致伸缩铁氧体粉状材料经压制成形、烧结而成的。由于材料电阻率高，可以整体压制，其主要结构形式如图6.3-10所示。

利用多个π形或Ⅰ形的铁氧体芯组合，可以获得不同的辐射面积，用以适应不同的加T处理需要。这种换能器的直流磁场是用加恒磁体的方法形成的。

图6.3-10 铁氧体磁致伸缩换能器

a)Ⅱ形铁氧体换能器 b）I形铁氧体换能器

(2)共振频率公式到了使压电片的极化强度增大的作用。极化强度的增大，使压电片沿极化方向产生伸长的形变。

2）外加电场与极化方向相反。反向电场将削弱压电片的极化强度，使得压电片沿极化方向产生缩短的形变。

利用这两种现象，将外加电场换为交变电场时，压电片就会产生与交变电场同频率的交变形变，从而使压电片两面向外辐射声波。当外加电场频率与压电片固有频率相同产生谐振时，压电片振动最大，声辐射也最强烈。

压电片厚度方向逆压电效应表达式为：

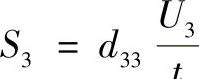
式中，S₃为沿厚度方向的伸缩应变；d₃₃为沿厚度方向的压电常数；U₃为沿厚度方向所加电压；t为压电片厚度。(www.xing528.com)

6.3.2.2 压电材料及其性能

压电材料是研制压电换能器的重要环节之一，目前常用的压电材料有以下两类：石英晶体和压电陶瓷。

1.石英晶体

石英晶体又称水晶，其性能稳定，不管是随温度，还是随时间性能的变化都很小，-190℃时压电常数仅比室温时下降1.3%，200℃以下时，压电常数几乎与温度无关。石英晶体的力学性能良好，易于切割、研磨和抛光加工，机械损耗小，机械Q值可高达10⁶。其介电常数较低，谐振时阻抗较高，广泛用来制作标准频率控制的振子及高选择性的滤波器。作为超声换能器材料可用来制作大功率发射器，并可在高温下工作。目前，尚未见到石英晶体用于超声加工换能器的报道。

2.压电陶瓷

压电陶瓷具有多方面的适应性，从物理性质的角度看，它是坚硬的，具有能够施加或承受很大应力的能力。而从化学性质的角度看，它是“惰性”的，不受潮湿和其他气候条件的影响。压电陶瓷材料的制作方法与绝缘陶瓷材料类似，简便易行，几乎可以做成任何需要的形状和尺寸，并可以方便地选择其极化方向，非常适合用于换能器的制作。压电陶瓷可以通过改变其化学组分及添加杂质来改变其性能，以适应各种不同的用途，其分类大致如下：

表6.3-3给出了几种常用的压电陶瓷材料及其性能特点。

表6.3-3 几种主要的换能器材料

（续）

6.3.2.3 压电换能器的结构形式、特点及频率公式

1.夹心式压电换能器

（1）夹心换能器的结构 由于压电陶瓷材料的抗拉强度低（抗压强度高），因此在某些场合不能直接用于发射大功率。为了解决这个问题，法国物理学家郎之万（Langevin）把压电材料夹持在两个金属块之间。通过夹持给压电材料加一定的预应力，使换能器工作时不致于受到大拉力（甚至不受到拉力），这样就可以实现大功率发射了。这种换能器叫夹心换能器，也叫郎之万型换能器。图6.3-15所示为螺杆夹心换能器的结构示意图。它由中央压电陶瓷堆、前后金属盖板、预应力螺杆、电极片及绝缘管组成。

中央陶瓷堆由若干压电陶瓷环组成，压电晶片间采用机械串联、电端并联的方法连接，如图6.3-16所示。相邻两片的极化方向相反，以保证压电陶瓷堆能协调一致地振动。晶片的数目一般成偶数，以便使前后盖板与同一极性的电极相连。否则，前后盖板与晶片之间要垫以绝缘垫。极化后的晶片要老化1～2个月才可使用。使用时，晶片表面要研磨，两面平行度要好，并加流动性好、易浸润的填充剂，以保持振动时机械耦合好。

图6.3-15 夹心换能器基本结构

1—后盖板 2—绝缘管 3—电极片 4—压电陶瓷片 5—螺杆 6—前盖板

图6.3-16 晶片排列法

晶片之间以及晶片与金属盖板间，通常用铍青铜片作为电极，其厚度为0.3～0.5mm。螺杆与晶片之间要用绝缘套管，以免高压打火。

前、后盖板一般采用钢、铝镁合金或硬铝，以及钛合金等金属材料制作。其要求是材料疲劳强度高、机械损耗低。而钛合金最为理想，但太昂贵。钢的损耗大，在大功率级下应避免使用。所以，最常用的是硬铝。加工时，结合表面要研磨，以保证良好的机械耦合。

螺杆需用高强度的螺栓钢制成，要求抗拉强度在800MPa以上。螺纹采用圆弧式。

夹心式压电换能器的另一种形式为涨力壳夹紧结构，是用一个带有螺纹的金属筒连接金属块，把压电套磁片夹紧，如图6.3-17所示。这种夹紧结构可用于制作大功率压电换能器。

对不同的应用对象，可设计不同形式的前盖板。如在大功率超声清洗设备方面，由于单个换能器的功率容量有限，因此需要由多个换能器组合而成。由于夹心式换能器Q值较高、频带较窄，所以需要挑选频率和阻抗都较接近的换能器配组，这给制造和维修都带来不小的麻烦。为解决这一问题，进一步改善与负载的匹配，可将前盖板做成喇叭形并在锥辐射面上钻许多孔，形成宽频带夹心式换能器，如图6.3-18所示。

图6.3-17 涨力壳结构

1—声耦合杆 2—预应力套 3—压电片 4—电极 5—声稳定件

图6.3-18 宽频带夹心式换能器

利用这种形式的换能器，在液体负载情况下，可降低Q值，增加带宽。例如，工作频率为20kHz，辐射面为ϕ78mm的清洗换能器，孔径可取ϕ5mm，孔心距为7mm，孔深为辐射块高度的一半，孔均匀分布。对40kHz，辐射面为ϕ50mm的清洗用换能器，孔径取ϕ3.5mm，孔心距取5.5mm。

在另外一些场合，如在超声打孔中，要把能量聚集到很小的面积上，此时前盖板可做成有利于能量集中的各种形式，如锥形、阶梯形、指数形等。

夹心式压电换能器的主要特点是：可以在十几千赫到几十千赫的低频段正常工作；由于夹紧结构加有预应力，增大了换能器的机械强度；有较好的温度特性。缺点是：结构比较复杂，理论设计也有一定难度；对同一换能器中所使用的两压电片，阻抗要进行选配。对大功率换能器，两压电片场强损耗也要求一致。

夹心式加预应力压紧结构压电换能器一般用于低频超声清洗、加工、搪锡、焊接、乳化等方面。

（2）夹心换能器的设计 设计时，首先要根据应用对象及所使用的功率大小决定所用晶片的直径及片数、前后金属盖板的形状，然后根据谐振条件算出前后盖板的长度，以满足某一要求的频率。

实际应用时负载对共振频率的影响很小，设计时可按换能器空载（即两端自由）进行计算。图6.3-19所示为圆柱形换能器，其长度等于半个波长，所以也叫半波振子。

图6.3-19 圆柱形换能器

a）基本结构 b）振幅分布

我们假定横向尺寸小于1/4波长，换能器作纵向振动。图6.3-19b中对应于S点的平面内，各质点的位移振幅为零，这个面叫做节面。通常设计换能器时是先确定节面位置，然后计算盖板长度。

节面可以设计在不同的位置，既可在后盖板中，压电陶瓷堆中，也可在前盖板中。通常取的位置有：后盖板与陶瓷堆交界面（以下称为节面在后），陶瓷堆中央（以下称为节面在中），陶瓷堆与前盖板的交界面（以下称为节面在前），以及在前盖板中某一位置。

1）圆柱形换能器。对如图6.3-19a所示的换能器，设前盖板、压电陶瓷堆及后盖板的特性阻抗分别为Z₁、Z₂、Z₃（Z_n=ρ_nc_ns_n，n=1、2、3，ρ_n、c_n、s_n分别是密度、声速和截面积），长度分别为l₁、l₂和l₃。频率方程可由等效传输线理论求得。其基本方法如下：

图6.3-20 等截面细棒阻抗变换

把换能器看作等效传输线，对应于自由端其阻抗为零，对应于节点处，其阻抗为无穷大。对均匀截面棒，如图6.3-20，其阻抗变换关系为

式中，Z₀=ρ₀c₀s₀为棒的特性阻抗；Z_L是右端的负载阻抗；Z_i是从棒左端看的阻抗；l是棒的长度，k是波数。

对变截面棒，其阻抗变换关系可用Mo¨bius变换方法，如图6.3-21所示。设W=Z_i/（ρcs₁），Z=Z_L/（ρcs₂），则有

式中，a、b、c、d是由变截面棒的形状决定的。例如，对于锥形棒：a

图6.3-21 变截面棒

阻抗的反变换为

根据上述方法，对图6.3-19所示的圆柱形换能器，其共振频率方程如下：

① 节面在后，前盖板的长度满足

式中ω=2πf，f是所要求的频率。

后盖板的长度满足：，即，1/4波长。

② 节面在中，前、后盖板长度相等并满足：

③ 节面在前，前盖板长度是1/4波长，即l=λ/4。后盖板长度满足：

④ 节面在前盖板中。设其与压电陶瓷堆前端面的距离是l_s，前盖板的长度为l_s+λ/4，则

后盖板长度满足：

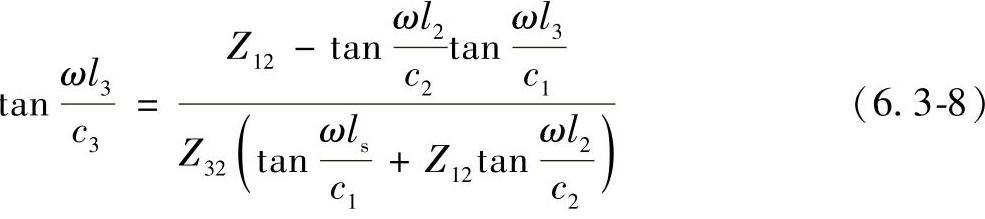
式中 Z₁₂=Z₁/Z₂，Z₃₂=Z₃/Z₂。

2）喇叭型换能器。对如图6.3-22所示的喇叭型换能器，即前盖板是锥形，后盖板是圆柱形。对于节面在后、节面在中、节面在前，后盖板长度的计算同前。下面只给出前盖板长度的计算。推导方法还是阻抗变换关系，只是要利用前面所述的圆锥形情况下的变换关系。

图6.3-22 喇叭型换能器结构

① 节面在后。前盖板满足方程

式中，；

图6.3-23 夹心换能器示意图

1、2、4、5—金属元件 3—压电元件 6、7—夹持螺杆

② 节面在中。只需在式（6.3-9）中把l₂变为l₂/2即可。

③ 节面在前。此时要求，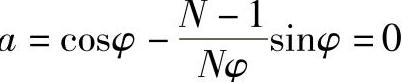

如考虑预应力螺杆对共振频率的影响，则计算结果更加精确。频率方程的求得同样是利用等效传输线理论。先以节面位置为界将换能器分为两部分，然后在每一部分中找一个基准面，利用对基准面传输线的机械阻抗的总和等于零的条件，得到两个谐振方程。如图6.3-23所示，考虑螺杆影响时，把换能器分为7个部分（按特性阻抗）。设压电陶瓷堆中心de是节面，由de面把换能器分为两部分Ⅰ和Ⅱ。

对于第Ⅰ部分，以b为基准面，向a看其阻抗为jZ₀₁tan（k₁l₁）；由b向右看，阻抗为-jZ₀₂cot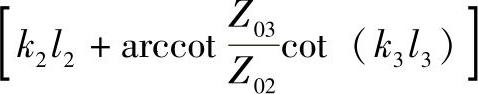

由于螺杆的阻抗为，按照总阻抗为零则有

对第Ⅱ部分，以g为基准面，同样的方法可得

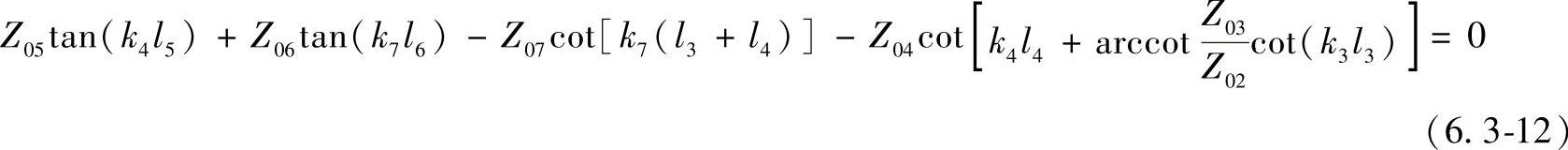
式中，Z_0n=（s_nρ_nc_n）、k_n、l_n分别为特性阻抗，波数及各部分长度。

2.其他几种典型的压电换能器的结构形式及频率公式

其他几种典型的压电换能器的结构形式及频率公式见表6.3-4。

表6.3 - 4 几种典型的压电换能器的结构形式及频率公式

（续）