影响放电腐蚀的关键因素分析

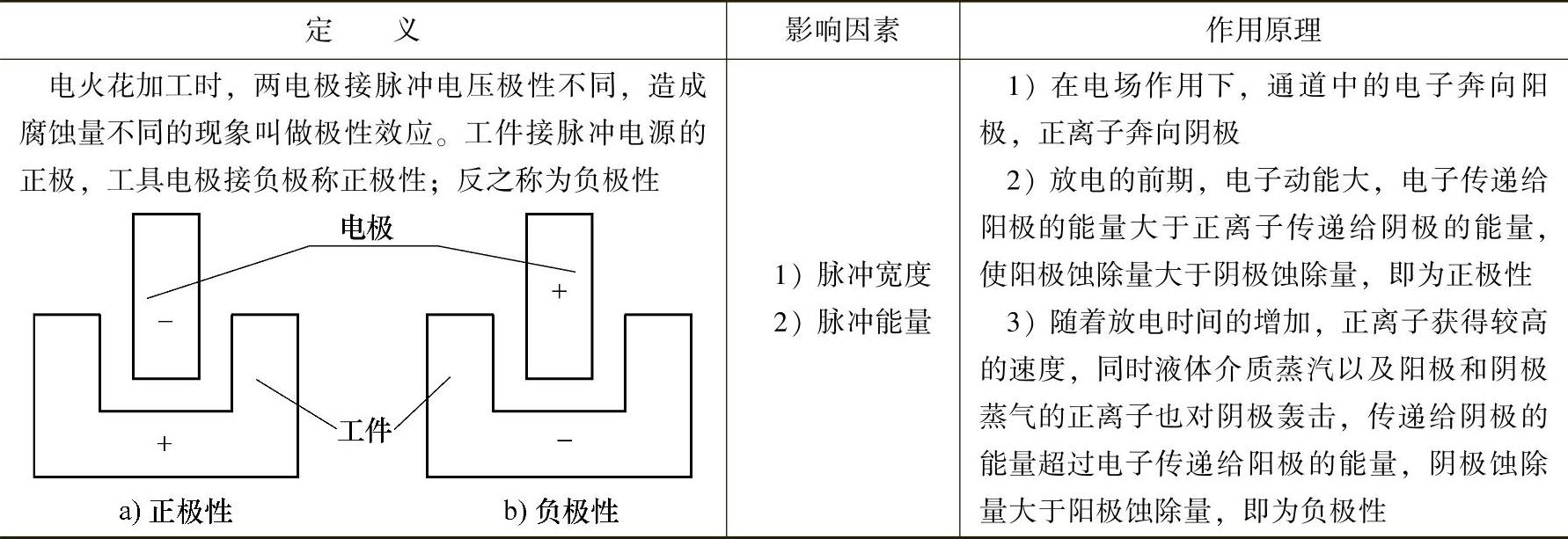
2.1.2.1 极性效应

极性效应的定义、影响因素及作用原理见表2.1-4。

表2.1 - 4 极性效应的定义、影响因素和作用原理

2.1.2.2 覆盖效应

1.定义及作用

在材料放电腐蚀过程中，一个电极的电蚀产物转移到另一个电极表面上，形成一定厚度的覆盖层，这种现象叫做覆盖效应。合理利用覆盖效应，有利于降低电极损耗。

在油类介质中加工时，覆盖层主要是石墨化的碳素层，其次是粘附在电极表面的金属微粒粘接层。碳素层具有很高的耐电腐蚀性，对电极表面有一定保护作用。粘接层为钢的微粒层，强度不牢，耐蚀性也不高，但也有补偿电极损耗的作用。碳素层的形成条件见表2.1-5。

表2.1 - 5 碳素层的形成条件

2.覆盖效应的影响因素

覆盖效应的影响因素及作用原理见表2.1-6。

表2.1 - 6 覆盖效应的影响因素及作用

2.1.2.3 间隙效应

1.间隙与间隙电压的关系

液体介质在小间隙脉冲放电时，极间距离与击穿电压的关系接近直线，间隙击穿电压梯度基本不变，如图2.1-2所示。也就是说，在最小击穿电压u_d与最大击穿电压u_k之间，间隙δ与间隙电压u呈线性关系。

2.间隙与加工速度和电极损耗的关系

在电极与工件的形状与材料已确定，且工作介质也已确定的条件下，两极间电火花加工就存在一个最佳放电间隙δ_j，间隙δ大于或小于δ_j则加工效果都不好，如图2.1-3所示。

1）当间隙δ小于δ_j时，放电蚀除量减小而影响了加工速度，同时间隙过小而不易排屑，致使放电短路的几率大大增加，使电极的损耗增加。

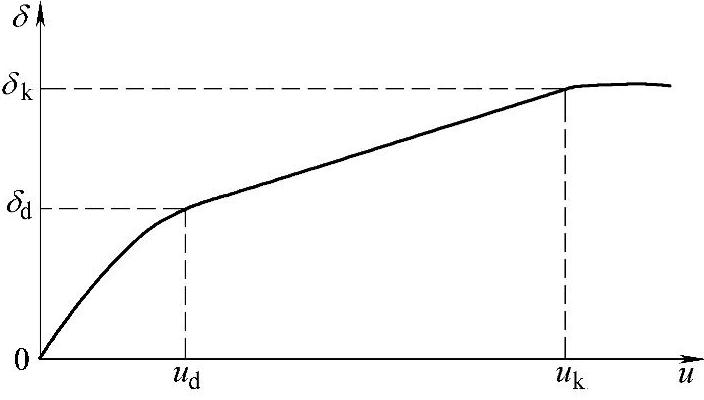
图2.1-2 间隙δ与间隙电压u的关系

2）当间隙δ大于δ_j时，致使放电空载几率大大增加，从而降低了加工速度。

2.1.2.4 面积效应

因加工面积变化引起加工速度v_w、电极损耗θ变化的效应称为面积效应，三者的关系如图2.1-4所示。

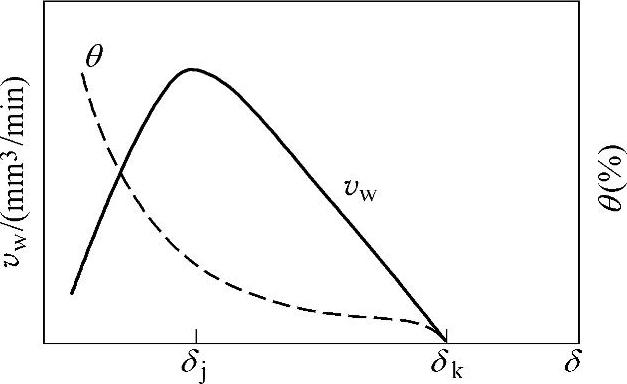
图2.1-3 间隙δ与加工速度v_w、电极损耗θ三者的关系

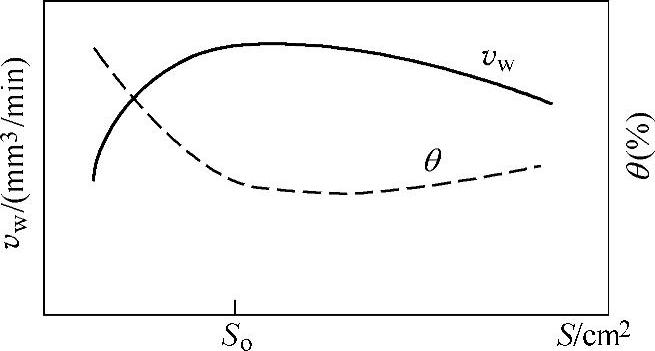
图2.1-4 面积效应

2.1.2.5 脉冲放电特性

1.单个脉冲能量

决定放电痕尺寸的主要参数是单个脉冲能量。放电电压越高，放电电流越大，放电时间越长，间隙中获得的单个脉冲放电能量就越大，单个脉冲能量用式（2.1-2）表示：

式中，W_o是单个脉冲能量；u是间隙瞬时放电电压；i是间隙瞬时放电电流；t是放电持续时间（脉冲宽度）。

2.放电痕尺寸与脉冲宽度和峰值电流的关系

在一定加工条件下，单个脉冲的放电电压变化不大，放电痕尺寸与脉冲宽度、峰值电流有下列经验公式（试验条件：铜电极加工钢件，负极性，脉冲宽度10～1000μs，电流峰值27～144A）：

式中，Ra是实测的表面粗糙度（μm）；K_R是常数，K_R=2.3；t_i是脉冲宽度（μs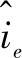）；是峰值电流（A）。

式中，D是实测的放电痕平均直径（mm）；K_D是常数，K_D=9×10^-3。(www.xing528.com)

式中，m_o是实测的单个脉冲蚀除量（g/脉冲）；K_m是常数，K_m=9.4×10^-11。

3.矩形波加工时的低损耗条件

矩形波宽脉冲、负极性加工时，体积损耗小于1%的条件如下：

铜电极加工钢件时：

粗加工（Ra为10～20μm）——；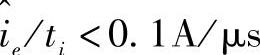

半精加工（Ra为0.63～1.25μm）——。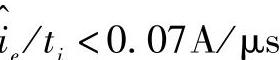

石墨电极加工钢件时：

粗加工（Ra为10～12.5μm）——；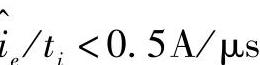

半精加公（Ra为1.25～2.5μm）——。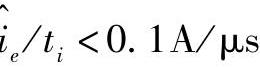

4.放电痕体积计算公式

根据放电热学理论，放电痕的体积V可由式（2.1-6）表示：

式中，Q是电极上脉冲放电区域积聚的热量；g是单位体积的相变全热；Φ是进入电极表面的单位热流，Φ=f（λ，t_i，W_o）；Φ′是电极体内单位表面因热传导而散失掉的热流，Φ′=f（λ，t_i）；S是放电痕表面积；λ是热导率；W_o是单个脉冲放电能量。

当t_i一定时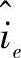，减小意味着W_o减小，即Φ减小，Q减小，故V亦减小。

2.1.2.6 介质效应

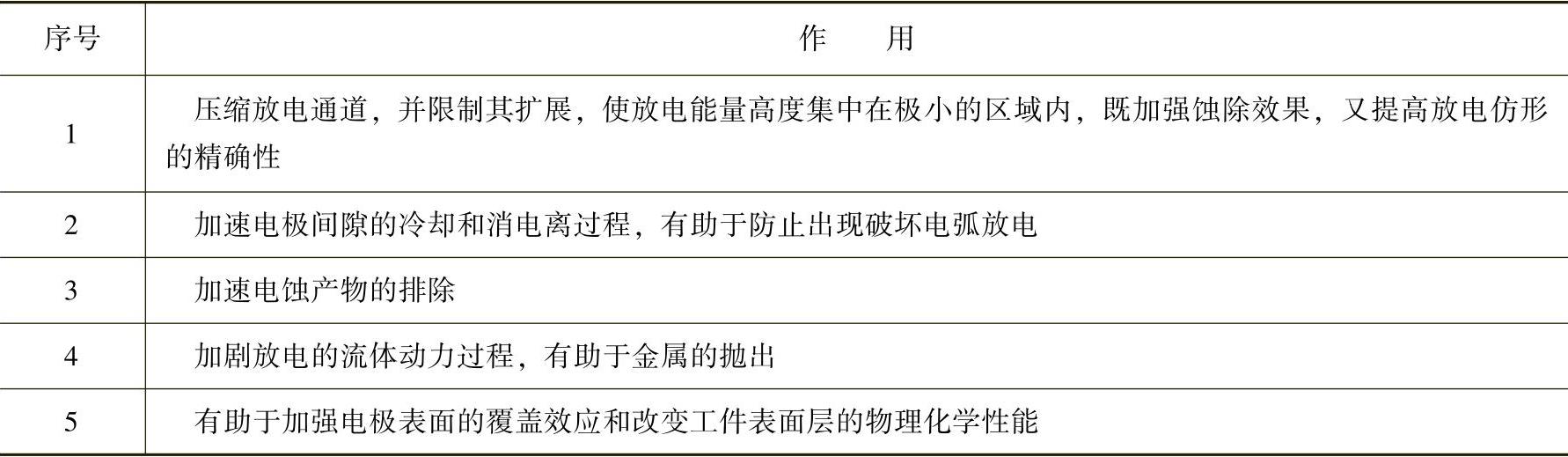
电火花加工一般在液体介质（工作液）中进行，工作液是参与放电蚀除过程的重要因素，它的种类、成分和性质势必影响加工的工艺指标，其主要作用见表2.1-7。

表2.1 - 7 工作液的主要作用

目前，电火花加工多采用石油产物介质做工作液。煤油粘度低，排屑条件较好，是应用较普遍的一种工作液。在大能量加工中，常采用燃点高的全损耗系统用油、变压器油、锭子油或者它们与煤油混合的工作液。在油中加入活化剂能够提高加工工艺指标，在油类介质中加入各种添加剂，亦能达到提高加工速度，降低损耗的目的。

采用水做工作液是值得注意的一个方向。在弛张式小能量脉冲电源下的试验表明，同样条件下，蒸馏水与煤油相比，阳极上放电痕直径减小5%～7%，深度减小18%～20%，放电痕体积平均减小20%左右；阴极上放电痕体积平均减小15%～20%，表面质量提高一级。

2.1.2.7 电极与工件材料特性

1.放电痕熔化体积

根据热过程理论，放电痕熔化体积V为

式中，Q是电极上脉冲放电区域积聚的热量；C是比热容；ρ是密度；T_r是熔点；T_o是原始温度；q_r是熔化热。

2.材料的耐蚀性

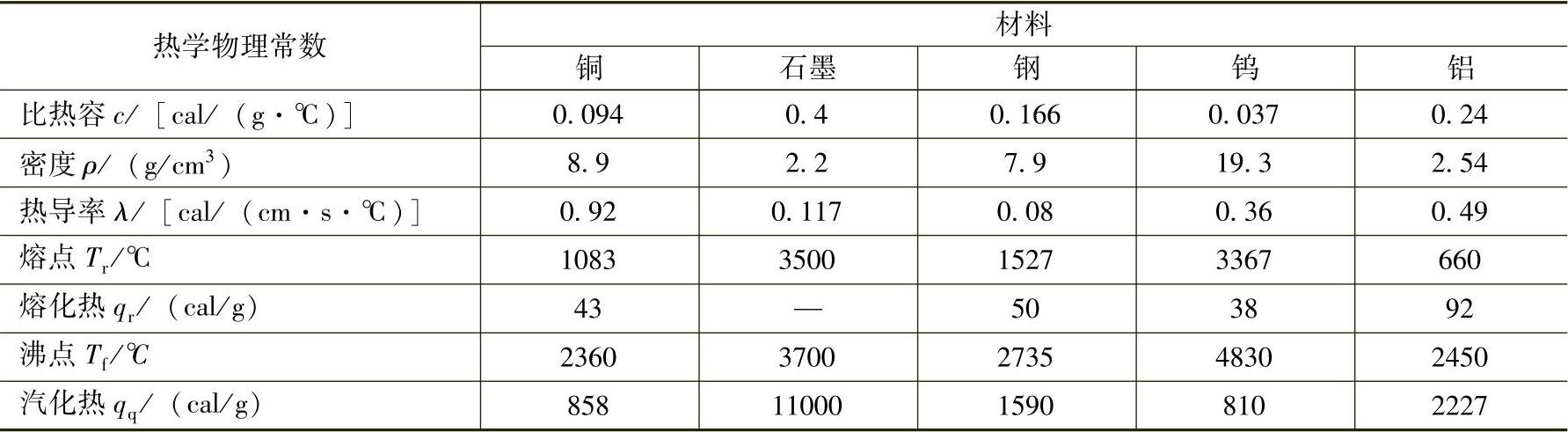
一般情况下，材料耐蚀性K可用热学物理常数来表示：

K=cρλT² （2.1-8）

表2.1-8所示为常用材料的热学物理常数。

注意，式（2.1-7）和式（2.1-8）并不适用于所有的金属和合金，因为耐蚀性还与材料在高温下的热学、力学及化学的稳定性有关，同时与材料的微观结构有关。

常见的耐蚀性材料及其特性见表2.1-9。

表2.1 - 8 常用材料的热学物理常数

注：1cal=4.18J。

表2.1 - 9 常见的耐蚀性材料及其特性

注：表中百分数为质量分数。