卷积码的Viterbi译码优化方法

卷积码的译码算法分为代数译码和概率译码两大类，共有3种主要译码算法。

1）门限译码。门限译码由J.L.Massey在1963年提出，这是一种利用码的代数结构的代数译码，类似于分组码中的大数逻辑译码。它的主要特点是算法简单，易于实现，译每个信息子组所需的运算时间是常数，即译码延时是固定的。

2）序列译码。1957年J.M.Wozencraft提出序列译码，1960年J.M.Wozencraft和B.Reiffen对其加以完善。1963年R.M.Fano对序列译码进行了重要的改进，这种改进的序列译码称为Fano算法。序列译码是基于码树图结构上的一种准最佳的概率译码，通常序列译码的延时是随机的，它与信道干扰情况有关。在工程中使用的序列译码主要是Fano算法。

3）Viterbi算法。1967年A.J.Viterbi提出另一种卷积码的概率译码法，称为Viterbi算法。1969年J.K.Omura证明Viterbi算法等价于求通过一个加权图的最短路径问题的动态规划解。1973年G.D.Forney认识到它事实上是卷积码的最大似然译码算法。Viterbi算法基于码的网格图，其运算时间是固定的，译码的复杂性（硬件或软件实现）均与v成指数增长。在码的约束度较小时，它比序列译码算法效率更高、速度更快，译码器也较简单。因而，自提出以来，无论在理论上还是在实践中都得到了极其迅速的发展，并广泛地应用于各种通信系统，特别是卫星通信和深空通信系统中。

目前应用的卷积码译码器主要是Viterbi译码器。

1.分支度量和路径度量

设（n₀，k₀，v）卷积码编码器的输入是L组长（含Lk₀个码元）信息序列m；编码器的输出是L+v组长（含（L+v）n₀个码元）码字c；码字c经过信道传输后，其接收码字是r。序列m、c和r的表达式分别为

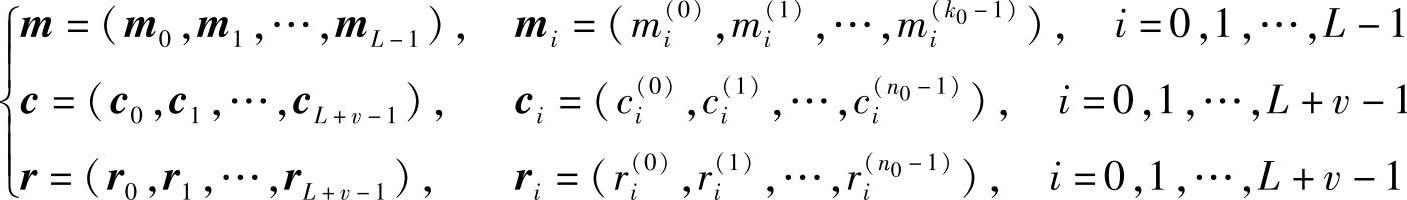
式中，m和c是二元序列。对于二元硬判决信道，接收码字的每个符号的值域是B：{0，1}；对于软判决信道，接收码字的每个符号的值域是B：R（其中R为实数集合），或者实数经过量化的输出。

定义6.73 设发送序列是c，接收序列是r，则似然函数定义为P（rc），对数似然函数定义为ln P（rc）。

对于离散无记忆信道，似然函数为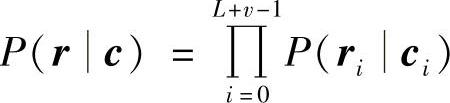，则相应的对数似然函数为

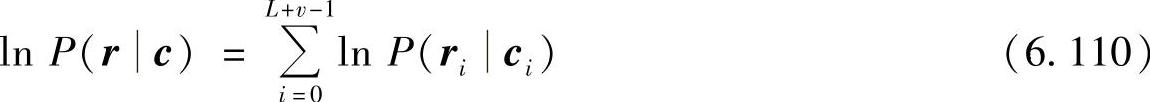
当采用最大似然译码算法时，要求在所有可能的码字序列中选取一条使式（6.110）的似然函数极大的码字序列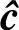作为发送码字序列的估计，则有

式中，C表示从零状态S₀出发、所有长度为L+v、最终回到零状态S₀的码字序列集合。译码器输出的码字序列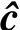，是网格图上使似然函数取最大值的一条路径，为此，给出定义：

定义6.74 网格图上的路径c的路径度量定义为ln P（r|c），记为λ（r|c）；分支c_i的分支度量定义为ln P（r_i|c_i），记为λ（r_i|c_i）。

用路径度量和分支度量的表示方法，式（6.110）可以改写成

式（6.112）表明，一条路径的路径度量为该路径上各分支度量之和。

定义6.75 网格图的一条路径c的前l个分支所构成的路径称为部分路径，其度量为部分路径度量，记为

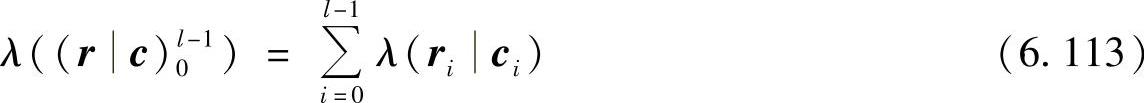
2.Viterbi译码算法

卷积码的最大似然译码就是要求在网格图上所有可能的路径中，选择一条有最大路径度量的路径作为译码序列的估值。当信息序列为L长时，可能的路径总数为2^k0L。可见，路径总数随路径长度L呈指数增加。若对每条可能路径计算相应的路径度量，然后比较其大小，并选取其中最大者，显然是不实用的。

考查图6.21的（2，1，2）卷积码的网格图。从状态S₀出发有两条路径，并在某一状态处汇合，以后这两条路径一直复合在一起。由于复合部分的分支度量对路径度量的贡献相同，所以，在汇合点处可以删去两条路径中前面的部分路径度量较小的一条。因此，在任何单元时间，对进入每一状态的所有路径，仅保留一条部分路径度量最大的路径。所保留的路径称为幸存路径。

由于（n₀，k₀，v）卷积码有2^k0v个状态，译码器最多需要保存2^k0v条幸存路径和相应的路径度量。由此可以归纳Viterbi译码的基本步骤如下：

1）在第j（j=v）单元时间以前，译码器计算所有长为v个分支的部分路径值，对进入2^k0v个状态的每一条路径都保留。

2）第v单元时间开始，对进入每一个状态的部分路径进行计算，这样的路径有2^k0条，选择具有最大部分路径值的部分路径为幸存路径，删去其他路径。若进入某个状态的部分路径中，有两条最大的部分路径值相同，则任选其一作为幸存路径。然后路径延长一个分支。

3）重复第2）步。若接收序列长为（L+v）n₀，其中，后v段是人为加入的全零码段，则译码进行到第L+v单元时间为止；否则，进行到所有接收序列进入译码器为止。

下面以两个例子进一步说明Viterbi译码的过程。

【例6.66】

对于图6.21所示网格图所描述的（2，1，2）卷积码，若接收序列为r=（00，01，00，10，00，00，00，01），要求从网格图中选取一条最大似然路径。(www.xing528.com)

解 在图6.22的（2，1，2）卷积码网格图中，分支上的数字表示接收序列与编码器分支上子码之间的Hamming距离，节点圆中的数字表示到达该状态幸存路径的部分路径度量，实线标记的路径是幸存路径，虚线标记的路径是未选中的路径，标有X的节点圆表示进入该节点的路径有相同的部分路径度量。

在2T单元时间以后，每个状态有两条路径进入，每条路径的部分路径度量等于前一单元时间出发状态的幸存路径度量与相应的分支度量的和。比较这两个和值，取其较小的为幸存路径值，对应的路径为幸存路径。

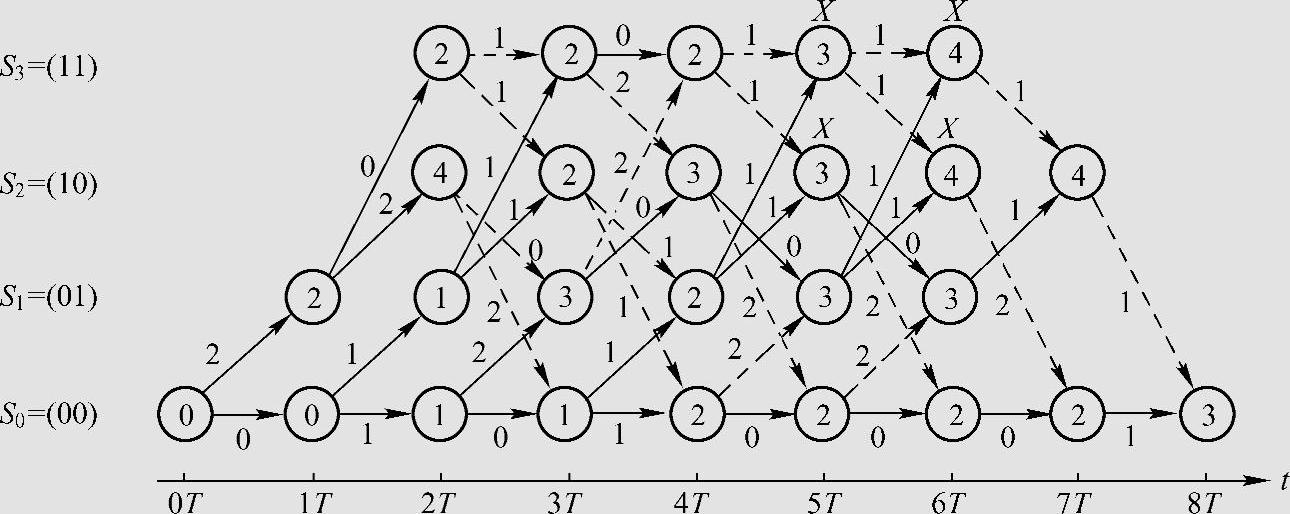
图6.22 Viterbi算法的示意说明

如在t=5T单元时间进入状态S₀的路径有两条，一条是从t=4T单元时间状态S₀通过一条分支度量为0的分支进入，另一条是从t=4T单元时间状态S₂通过一条分支度量为2的分支进入。这两条路径的部分路径度量分别为2和5，取其中较小者对应的为幸存路径，同时记下该单元时间到达状态S₀的幸存路径值2。而进入状态S₂的两条路径的部分路径度量相等，则可以任意保留其中一条。依此方法，完成路径搜索。最后到t=8T单元时间，最后的一条幸存路径为S₀→S₀→S₀→S₀→S₀→S₀→S₀→S₀→S₀，也就是说，判定发送的是全零序列m=（0，0，0，0，0，0，0，0）。

【例6.67】

（3，1，2）卷积码的生成多项式矩阵为G（x）=[1+x 1+x² 1+x+x²]。消息序列的长度L=6，假定接收序列为r=（110，010，011，110，011，111，001，011），要求从网格图中选取一条最大似然路径。

解 图6.23是（3，1，2）卷积码的状态转移图和网格图，图中的标注方法与例6.66相同。最终的幸存路径为S₀→S₁→S₃→S₃→S₂→S₀→S₁→S₂→S₀，也就是说，判定发送序列为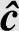=（111，010，001，110，011，111，101，011），相应的消息序列为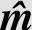=（1，1，1，0，0，1，0，0）。

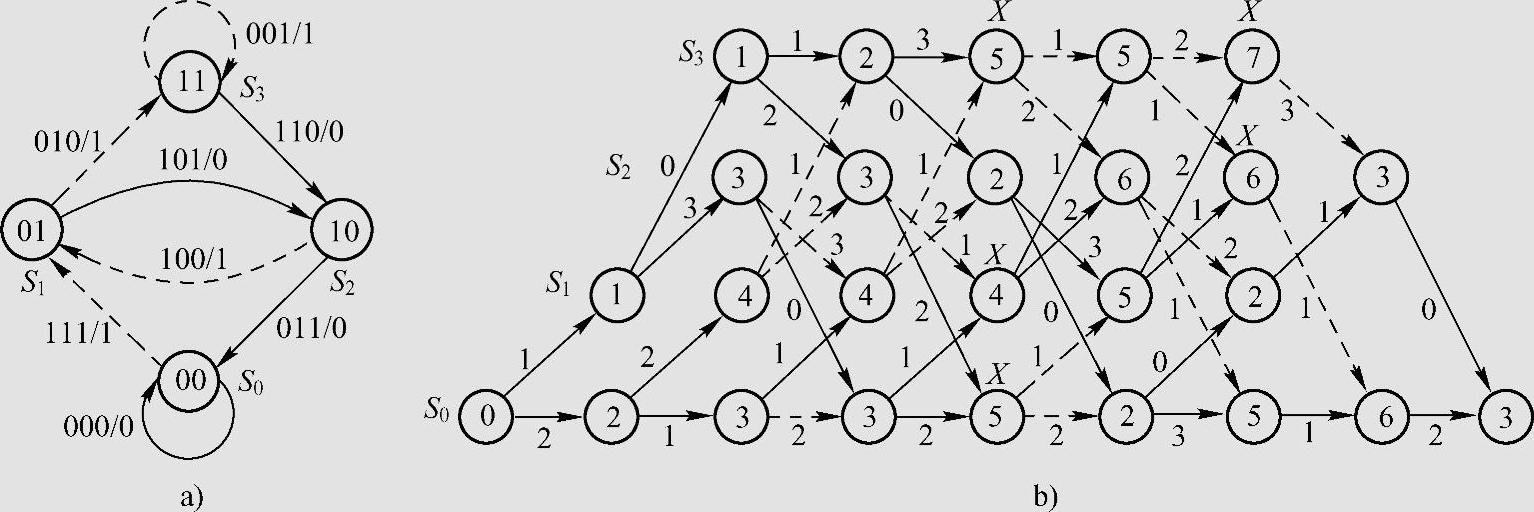
图6.23 （3，1，2）卷积码的Viterbi译码过程

a）状态转移图 b）网格图

3.实现Viterbi译码算法的一些具体考虑

在实现Viterbi算法时，还存在一些具体问题。例如，译码器存储的考虑、路径存储的截断问题、分支度量量化问题和Viterbi译码器的同步问题等，下面分述之。

（1）译码器存储长度

由于编码器状态图中有2^k0v个状态，对每个状态必须提供存储器来寄存幸存路径及其度量值。由于状态数随v呈指数率增长，所以v约取10时，即被认为是相当大的，再增大v值被认为是不合适的。由于卷积码中的n₀v相当于分组码中的码长，由信道编码定理知，当码速率小于信道容量时，可以增大码长来使误码率趋于零；在卷积码中增大v也可以使误码率降低。由于v不能取得很大，所以Viterbi算法不可能做到使错误概率任意小。

大多数情况下，大约7dB的编码增益和10^-6的错误概率被认为是实际的极限。当然，错误概率的精确值取决于码率、码的自由距离、信道信噪比和解调器输出量化等多种因素。

（2）路径存储的截断

Viterbi译码的标准算法要求路径都回到初始零状态，才能最后判决出最优路径，这要求在传输中最后添加k₀v个0。于是使得传输速率损失了v/（L+v）。这是一种浪费，虽然增加L值可以减小这种资源的损失，但采用较大L的困难在于每个状态用于寄存幸存路径和度量值的存储器大小随着L正比增大，对于很大的L，这显然是不实际的。另外L增大也使译码延时增大，所以必须作一些折中。

通常的办法是截断译码器的路径存储，即对每条幸存路径只寄存其最近的τ个信息数据，其中τ≪L。因此，译码器处理了接收序列的前τ组数据后，译码存储器就满了。这时就必须作出强制性判决，确定第一个信息子组，并作为译码器最终判决输出，然后从存储器中删去第一个信息子组，腾出空间以暂存新来到的幸存数据，如此过程重复进行。

在任何k单元时间（k≥τ），强制性判决可以有以下几种可能的方式进行：

1）在2^k0v条幸存路径中任选一条，该条路径中第k-τ单元时间的数据为译码输出。

2）在2^k0v个可能的第k-τ单元时间数据中，选一个出现次数最多的数据为译码输出。

3）在2^k0v条幸存路径中，选最大部分路径值的路径的第k-τ单元时间数据为译码输出。

若采用以上3种强制截断的方式来译码，显然已不再是最大似然译码了，它们的性能要劣于最大似然译码。但是，一条路径与正确路径分离的跨度越大，则这条路径在分离跨度上积累的路径度量会越小，于是一旦该路径与正确路径复合，则被淘汰的概率很高。也就是说，在译码过程中与正确路径分离跨度很大的不正确路径作为幸存路径的概率很小。经验和分析表明，若τ是编码存储v的5倍或更多，则在k单元时间所有2^k0v条幸存路径，实际上至晚在k-τ单元时间，就已经合并成一条。所以对于这3种强制性判决方法，性能差异很小，与最大似然译码差别也不大。采用路径截断后每个状态用于寄存幸存路径的存储器容量需要k₀τ位。

（3）译码器的同步

事实上，译码器不总是能从编码器置成全零状态之后传送的第0子码开始工作的。译码器可能从一个未知的编码状态开始工作，也就是说，译码器可能从编码网格图中间任何某单元时间开始工作。这时译码器的所有状态寄存器首先置零；每个状态下的幸存路径不是起始于同一个起始状态，而是起始于2^k0v个不同初态。G.D.Forny证明大约经过5v个分支后这些幸存路径就会汇合。在采用截断路径存储译码器中，开始的5v个判决是不可靠的，通常可以丢弃，大约5v个分支后，起始分支不同步的影响可以忽略不计，以后的判决可认为是正确的。

Viterbi译码还要求位同步，也就是说，译码器必须知道相继收到的n₀个接收符号中，哪一个是分支上第一个符号。一般在正确的位同步条件下，正确路径的度量明显比其他幸存路径大，如果位同步不正确，则所有的幸存路径的度量没有明显差别，所以如果译码工作一段单元时间后，发现幸存路径的度量没有明显差别，就及时改变位同步假定，重新译码，直到获得正确位同步为止。

（4）分支度量的量化精度

在BSC（二元对称信道）上，分支度量就是Hamming距离，这是整数度量；在无量化的加性高斯白噪声信道上分支度量是一个实数值，这对应一个无量化纯软译码。如果把接收数据量化成Q电平，则量化后的接收符号可以用Q元整数矢量来表示。仿真研究表明，8电平（Q=8）量化时的性能和无量化理想情况下的性能仅相差0.25 dB。而8电平量化的软译码比Q=2（即BSC情况）硬译码的性能要好2 dB。