卷积码的描述方法详解

卷积码的描述有矩阵法、多项式法、树图法、状态图法和网格图法等。采用何种方法描述卷积码与其译码方法有很大关系。在代数译码中，使用矩阵法描述便于理解；而在概率译码中，使用树图或网格图描述则更清晰。本节分别讨论这些描述方法。

1.卷积码的矩阵和多项式描述

【例6.58】（续例6.56）

设图6.15的（2，1，3）卷积码编码器的初始状态为零，输入和输出信息序列为

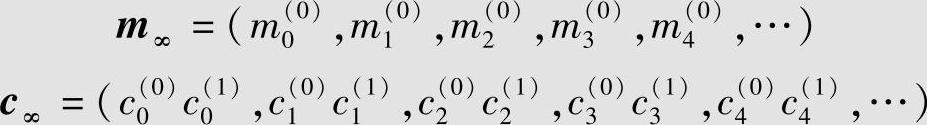
由图6.15中的编码规则，得到下列编码关系式：

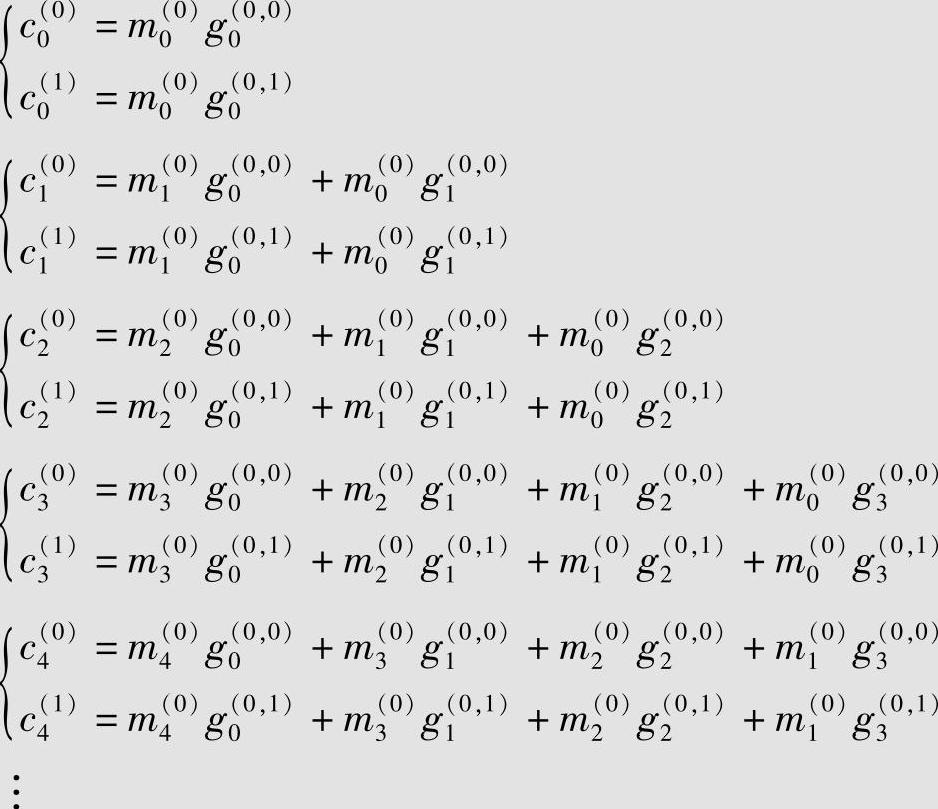
将上面的方程组写成矩阵形式为

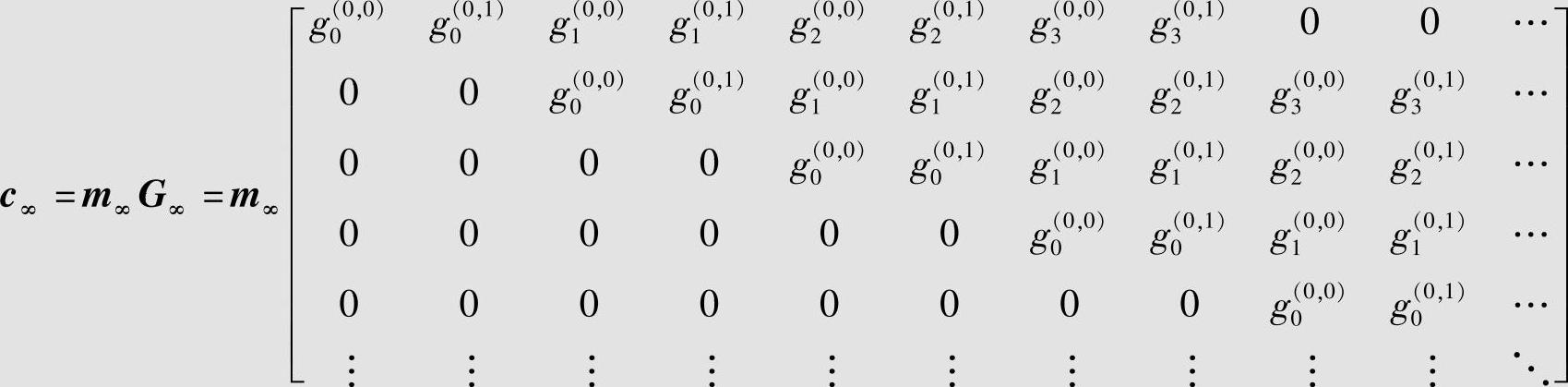
式中

设信息序列为m=（1，1，0，1，0，0，1），则对应的码字为c=mG_∞=（11，10，10，11，10，11，00，01，11，11）。

【例6.59】（续例6.57）

用类似例6.58的方法，可以得到图6.16的（3，2，2）编码器的编码方程为c_∞=m_∞ G_∞，其中

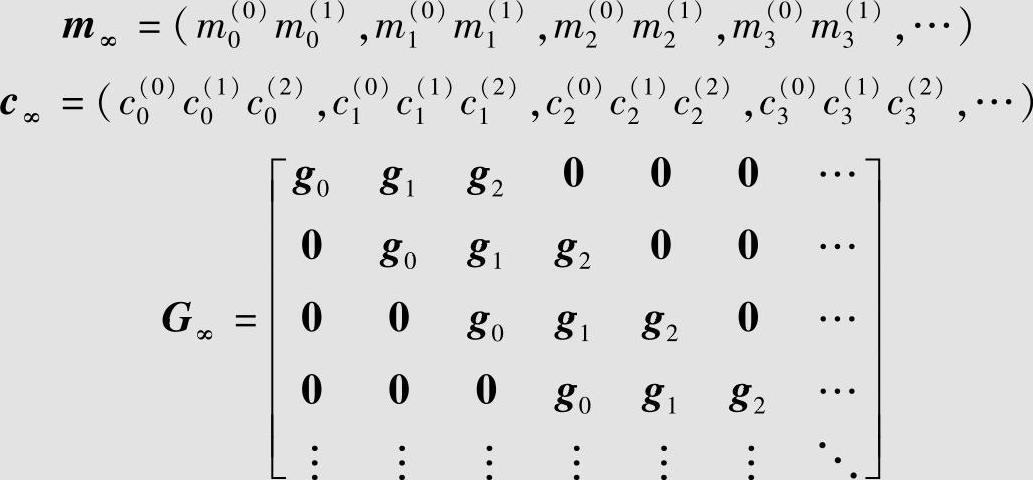
式中

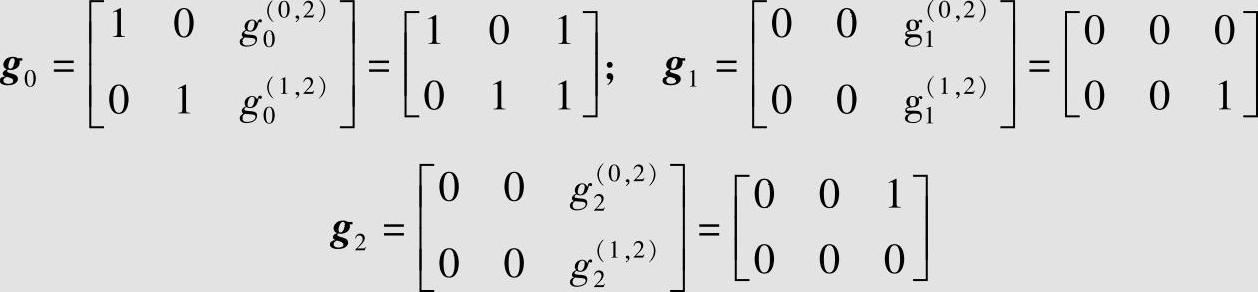
设信息序列为m=（11，01，10，01，00，01，11），则对应的码字为c=mG_∞=（110，010，101，011，000，011，111，001，001）。

由上面的两个例子可以看出，卷积码的编码完全由矩阵G_∞描述。

定义6.69 （n₀，k₀，v）卷积码的生成矩阵G_∞为

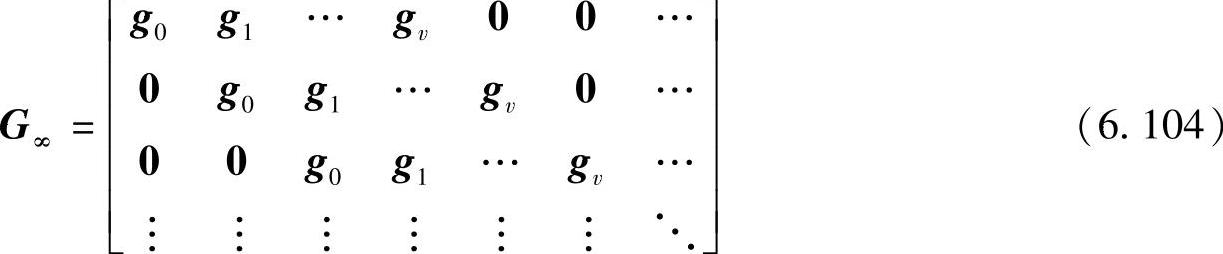
式中，g₀，g₁，…，g_v是k₀×n₀阶矩阵；0是k₀×n₀阶全0矩阵。

利用式（6.104）的生成矩阵进行编码，当输入的信息序列是有头无尾的半无限序列时，对应的码序列也为半无限序列。

在式（6.104）的生成矩阵G_∞中，若第一行的v+1个k₀×n₀阶子矩阵g₀，g₁，…，g_v确定以后，G_∞也就确定了。为此，给出定义：

定义6.70 G_∞的第一行定义为码的基本生成矩阵，用符号g_∞表示，即

g_∞=[g₀g₁…g_v00…]（ 6.105）

如果用延迟算子x（或用D）表示卷积码编码过程中的一个时间单元（对应码字为n₀个码元，对应信息组为k₀个码元）的延迟，则式（6.104）的生成矩阵G_∞可以写成

g_∞完全由前面v+1段的值g₀，g₁，…，g_v决定，从第v+2段起均为0。而g_i（i=0，1，…，v）由k₀n₀个数字决定，若把g_∞中前v+1段g₀，g₁，…，g_v中的每一段的第i，j位置的数字g_k^（i，j）（i=0，1，…k₀-1；j=0，1，…，n₀-1；k=0，1，…，v），用k₀n₀个多项式表示，则给出定义：

定义6.71 （n₀，k₀，v）卷积码的子生成多项式（或子生成元）定义为

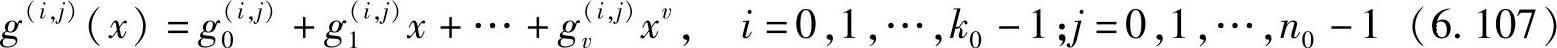
式中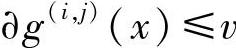，，g^（i，j）（x）的系数序列g^（i，j）=（g₀^（i，j），g₁^（i，j），…，g_v^（i，j））称为子生成序列（简称生成序列）。

g_∞完全由式（6.107）确定。因此，只要码的生成序列确定，则码的生成矩阵也就确定了。将子生成多项式写成多项式矩阵形式，就得到了如下定义：

定义6.72 （n₀，k₀，v）卷积码的生成多项式矩阵（或变换矩阵）G（x）定义为

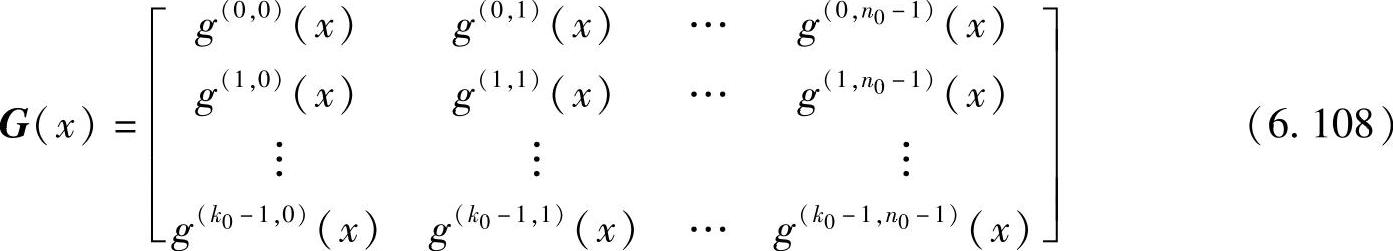
利用生成多项式矩阵可以实现卷积码的编码。方法如下：把信息序列m=（m₀，m₁，…）写成x的多项式形式m（x）=[m^（0）（x）m^（1）（x）…m^（k0-1）（x）]，相应的码序列c=（c₀，c₁，…）也写成x的多项式形式c（x）=[c^（0）（x）c^（1）（x）…c^（n0-1）（x）]，则有

c（x）=m（x）G（x） （6.109）

【例6.60】（续例6.56）

由图6.15的（2，1，3）卷积码编码器知，该码的子生成元为

g^（0，0）（x）=1+x²+x³，g^（0，1）（x）=1+x+x²+x³

则该码的生成多项式矩阵为

G（x）=[g^（0，0）（x）g^（0，1）（x）]=[1+x²+x³ 1+x+x²+x³](www.xing528.com)

若信息序列为m=（1，1，0，1，0，0，1），对应的信息多项式为m（x）=1+x+x³+x⁶，则码多项式为

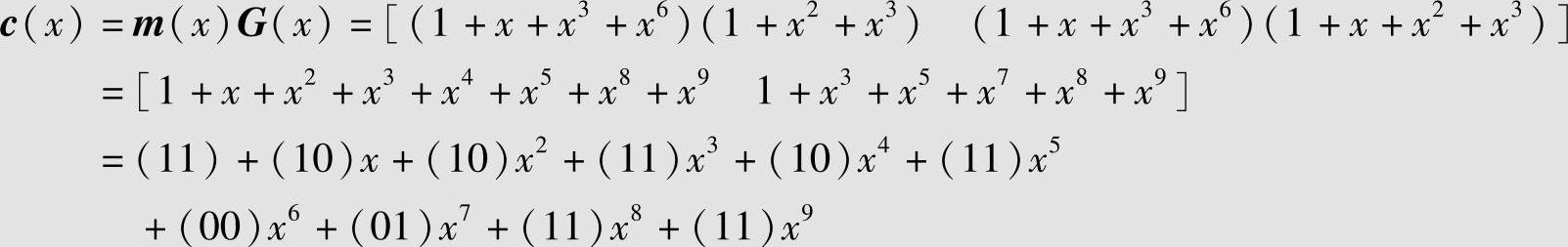
码多项式c（x）对应的码序列为c=（11，10，10，11，10，11，00，01，11，11），与例6.58相同。

【例6.61】（续例6.57）

由图6.16的（3，2，2）卷积码编码器知，该码的子生成元为

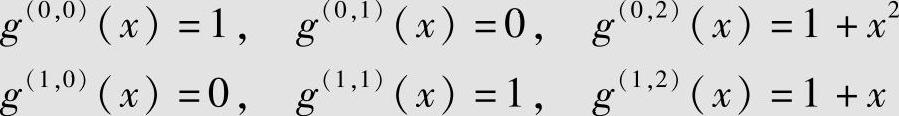
则该码的生成多项式矩阵为

若信息序列为m=（11，01，10，01，00，01，11），对应的信息多项式为m（x）=[m（^0）（x）m^（1）（x）]=[1+x²+x⁶1+x+x³+x⁵+x⁶]，则码多项式为

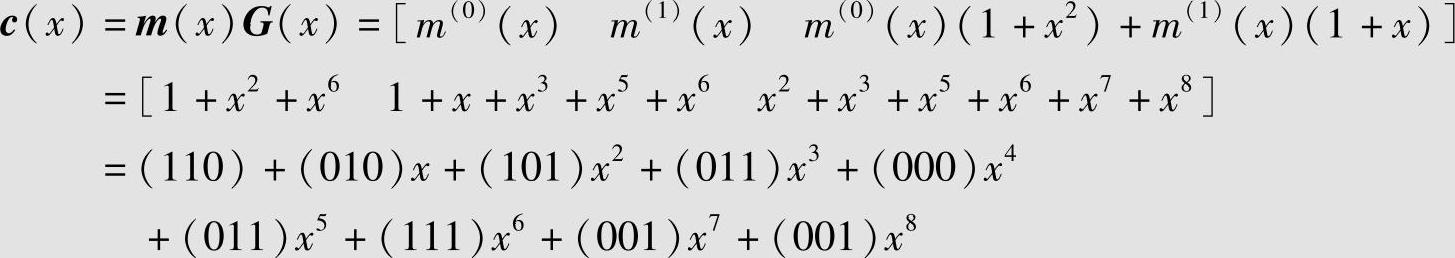
c（x）对应的码序列为c=（110，010，101，011，000，011，111，001，001），与例6.59相同。

由以上关于生成矩阵的讨论可以看到，它们与码的生成序列g（i，j）有密切的联系。所以，在卷积码的应用中，经常是给定码的生成序列g（i，j）。有了生成序列后，就可以确定卷积码的编码电路及矩阵表示式。

【例6.62】

给定（2，1，2）卷积码的子生成多项式g（0，0）（x）=1+x+x²，g（0，1）（x）=1+x²，则该码的生成多项式矩阵G（x）为

G（x）=[1+x+x²1+x²]

这是一个非系统码。子码中第1个码元由g^（0，0）（x）决定，即由此单元时间输入的信息元与前1个和前2个单元时间输入信息元的模2加；第2个码元由g^（0，1）（x）决定，是此单元时间输入的信息元与前2个单元时间输入信息元的模2加。图6.18是该码的编码器。

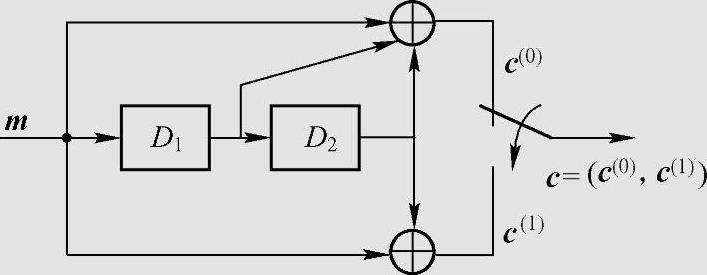
图6.18 （2，1，2）非系统卷积码编码器

2.卷积码的树图描述

如前所述，若（n₀，k₀，v）卷积码编码器的输入序列是半无限长序列，则它的输出序列也是半无限长序列。这种半无限长的输入/输出编码过程可以用半无限树图来描述。下面以例6.62的卷积码来说明卷积码的树图描述方法。

【例6.63】（续例6.62）

图6.18是（2，1，2）非系统卷积码的编码器，该电路有两个寄存器。用寄存器的内容表示该单元时间编码器的状态，共有4个状态S₀=（D₂D₁）=（00），S₁=（D₂D₁）=（01），S₂=（D₂D₁）=（10），S₃=（D₂D₁）=（11）。在第t单元时间，编码器的输出由该单元时间编码器的状态和输入数据决定，同时当前单元时间的状态和输入也决定了下一单元时间的编码器状态。设编码器的初始状态为S₀，相继的输入序列为m=（m₀，m₁，m₂，…），则整个编码过程可以用图6.19所示的码树表示。

在码树中的某一节点处，若输入0，则码树向上走一分支；若输入1，则码树向下走一分支。在每条分支上的2位数字表示此时编码器输出的两位编码数据，即一个子码。

编码时码树从根节点状态S₀出发，若m₀=0，码树走上面分支，输出子码（00），进入状态S₀；若输入m₀=1，码树走下面分支，输出子码（11），进入S₁状态。当第2个信息数据m₁输入时编码器已处于状态S₀或S₁，若编码器处于状态S₀，则m₁=0或1，编码器进入状态S₀或S₁，同时输出子码（00）或（11）；若编码器处于状态S₁，则由m₁=0或1，编码器进入状态S₂或S₃，同时输出子码（10）或（01）。如此继续，在码树上从根节点出发，从一个节点走向下一个节点，演绎出一条路径，而由组成路径的各分支所标记的两位输出数据所组成的序列就是编码器的码字序列。每一个输入消息序列对应唯一的一条路径，也就对应唯一的输出码字序列。

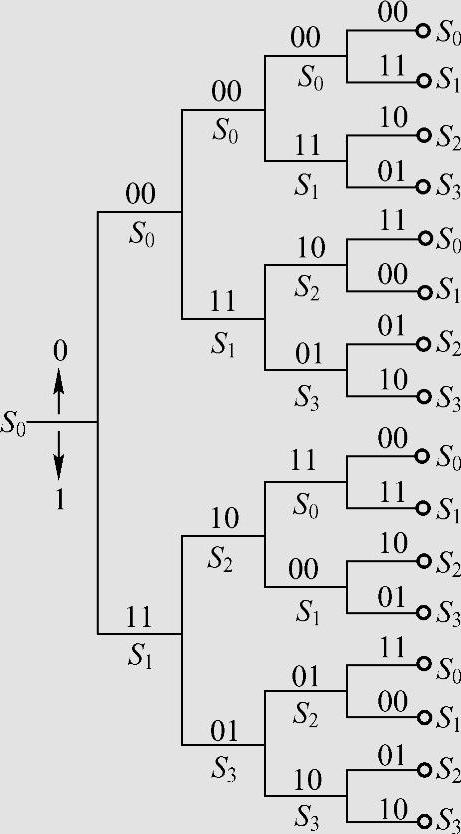
图6.19 （2，1，2）卷积码的码树图

对于一般的（n₀，k₀，v）卷积码，从每个节点出发2^k0条分支，每条分支上标有n₀位编码输出数据，最多可能有2^k0v种不同状态。

3.卷积码的状态图描述

实际上卷积码编码器是一个有限状态机，因此可以用状态转移图来描述。下面也以例6.62的卷积码来说明卷积码的状态图描述方法。

【例6.64】（续例6.62）

图6.20是图6.18的（2，1，2）卷积码编码器的状态图。在图6.20中斜线后的数字表示输入的信息元，斜线前面的数字表示编码器输出的子码。为清晰起见，对应于输入信息0时图中的转移支路用实线表示，对应于输入信息1时图中的转移支路用虚线表示。可以看出，若编码器初始状态处于S₀，输入信息元1时编码器从S₀转移到状态S₁，并输出子码（11）；若输入信息元0，则仍停止在状态S₀，输出子码（00），如此等等。随着信息元的不断输入，编码器的状态不断转移，并输出相应的子码，组成对应于输入信息序列的一个码序列。若输入信息序列m=（1，1，0，1，1，1，0，0），则编码器的状态变化依次是S₀→S₁→S₃→S₂→S₁→S₃→S₃→S₂→S₀，对应的输出码序列是c=（11，01，01，00，01，10，01，11）。

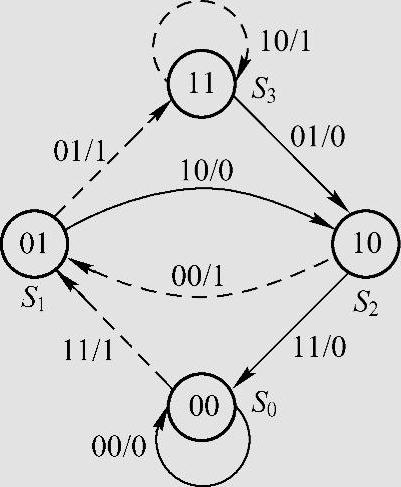
图6.20 （2，1，2）卷积码的状态图

4.卷积码的网格图描述

虽然状态图能表示卷积码编码器在不同的输入信息序列下，编码器各个状态之间的转移关系，但并不能表示出编码器状态转移与时间的关系，为了表示这种关系，可以采用网格图。网格图也称为篱笆图，它在Viterbi译码中特别有用。网格图既保持了树图的时序展开性，同时又克服了树图复杂的缺点，是一种简洁的表示方式。下面还以例6.62的卷积码来说明卷积码的网格图描述方法。

【例6.65】（续例6.62）

图6.21是L=6时图6.18的（2，1，2）卷积码的状态转移时间关系图，即网格图，L表示输入的信息子组数。该图由节点和分支组成，共有L+v+1=9个节点（或时间单位），分别标以0T～8T。若编码器从状态S₀开始并结束于状态S₀，则最初v=2个节点（0T和1T），对应于编码器由状态S₀出发往各个状态的转移，此过程仅经历部分节点（节点S₁）；最后v个节点（7T和8T），对应于编码器由各状态返回到状态S₀，此过程也仅经历部分节点（节点S₂）。因此，在开始和最后的v个节点，编码器不可能处于任意状态，只能处于某些特定状态之一。若输入与例6.64相同的信息序列m=（1，1，0，1，1，1，0，0），则由编码器输出的码序列为c=（11，01，01，00，01，10，01，11），它相应于网格图中用粗线表示的一条路径，结果与例6.64相同。

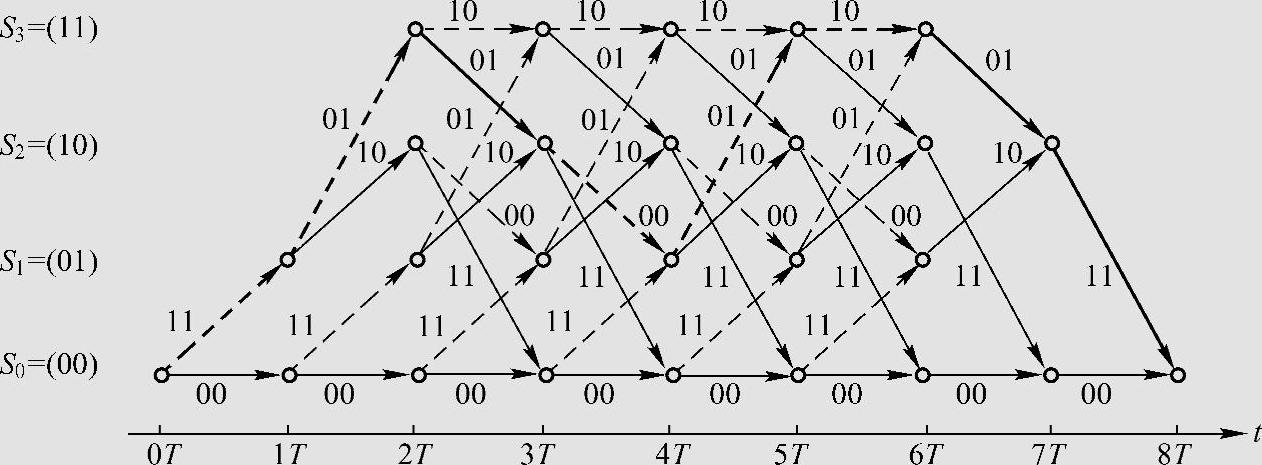
图6.21 （2，1，2）卷积码L=6时的网格图

网格图的第1层各个节点都代表移位寄存器处于状态S₀，第2层、第3层和第4层的各节点分别表示状态S₁、S₂和S₃。图中每个状态节点都有两个输入和输出分支，在某一单元时间i，离开某一状态的虚线分支（上面分支）表示第i单元时间输入编码器的信息m_i=1，而实线分支（下面分支）表示输入信息m_i=0。该分支旁标出的n₀=2位数字表示第i单元时间编码器所输出的子码c_i。因而，网格图上的每一条路径都对应不同的信息序列，同时也给出不同的输出码序列。由于所有可能的输入序列共有2^k0L个，因而网格图中可能有的路径也有2^k0L条，它相应于不同的2^k0L个（L+v）n₀长码序列。

一般情况下，（n₀，k₀，v）卷积码编码器共有2^k0v个状态，若输入的信息序列长度是k₀L+k₀v（后k₀v个码元全为0），则进入和离开每一状态各有2^k0条分支，在网格图上有2^k0L条不同的路径，相应于编码器输出的2^k0L个码序列。