卷积码基础概念简介

卷积码是与分组码相对应的另一大类纠错编码，在与分组码同样的编码效率下，卷积码的性能优于分组码；在相似的纠错能力下，卷积码的实现比分组码简单。所以，卷积码是一种广泛应用的码类，它更适用于前向纠错系统。

【例6.56】

图6.15是（2，1，3）非系统卷积码编码器。编码过程如下：若第i单元时间输入编码器的信息元为m_i，且移位寄存器内的数据右移一位，则m_i与前3个单元时间送入的信息元m_i-1、m_i-2和m_i-3按图6.15中指定的规则运算，输出此单元时间的2个码元c_i^（0）和c_i^（1），并组成子码c_i=（c_i^（0），c_i^（1）），其中

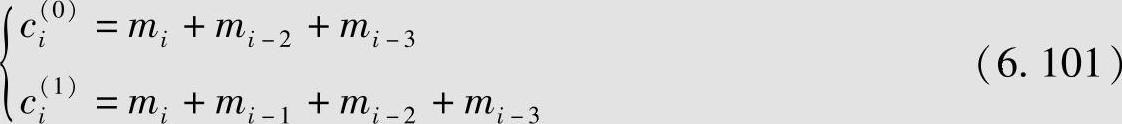
第i+1单元时间输入编码器的信息元为m_i+1，输出与此单元时间相应的2个码元

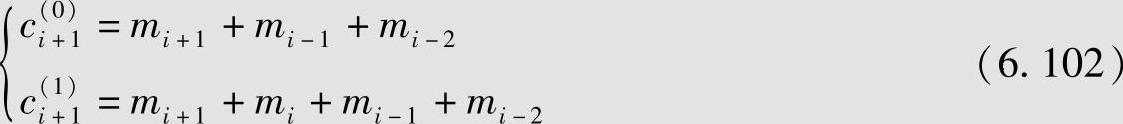
并组成子码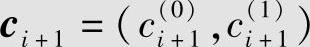，如此等等。在每一单元时间送入编码器k₀（此例为1）个信息元（称为信息子组），编码器就送出相应的n₀（此例为2）个码元。这一组n₀个码元组成卷积码的一个子码，子码有时也称为码段或子组。

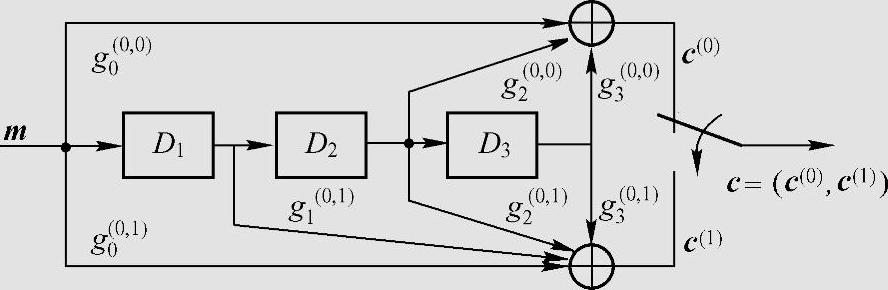
图6.15 （2，1，3）卷积码编码电路

该（2，1，3）非系统卷积码的编码运算式（6.101）或式（6.102）可以用矩阵形式表示，如式（6.101）可以写为

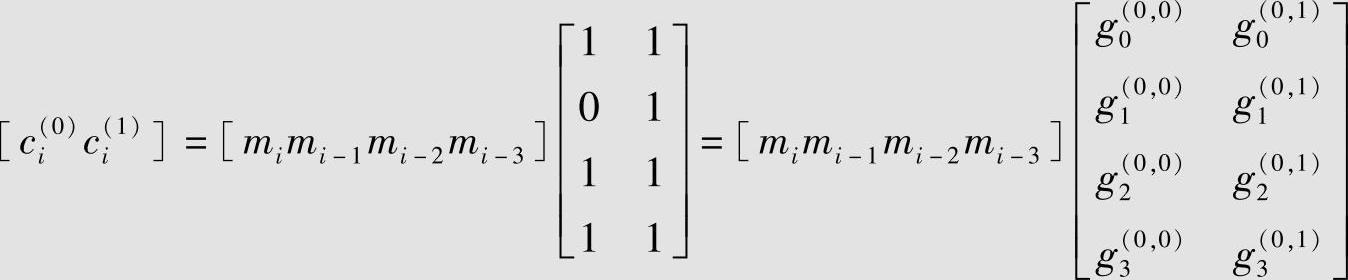
可见，卷积码编码方程的系数矩阵仅与编码器的连接方式有关，或者说，卷积码编码器仅由编码方程的系数矩阵确定。

【例6.57】

图6.16是（3，2，2）系统卷积码编码器。若第i单元时间并行输入编码器一组k₀（此例为2）个信息元m_i^（0）和m_i^（1）（记为m_i=（m_i^（0），m_i^（1）），也称为信息子组），且移位寄存器内的数据右移一位，则m_i^（0）和m_i^（1）直接输出（由于该码是系统码），同时m_i与前2个单元时间送入的信息元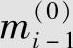、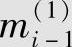和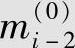、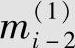按图6.16中指定的规则运算，输出此单元时间的1个校验元p_i，并组成子码c_i=（c_i^（0），c_i^（1），c_i^（2））=（m_i^（0），m_i^（1），p_i），其中

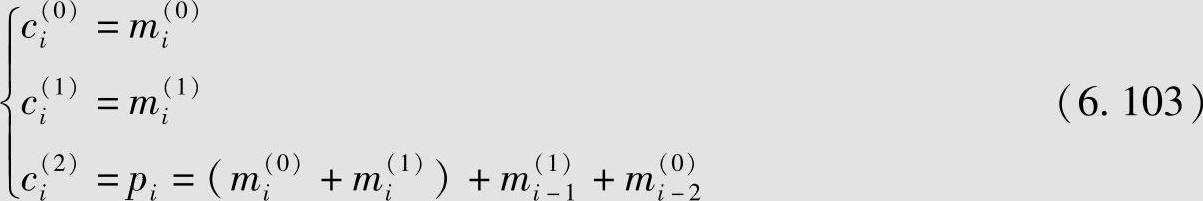
或写成(www.xing528.com)

用类似方法可以编出其他子码。该编码器在每一时间单位送至编码器k₀个信息元，编码器就送出相应的n₀（此例为3）个码元，并组成一个子码。该例中的每个子码有一个重要的特点，即子码的前两个码元为信息元m_i^（0）和m_i^（1）。

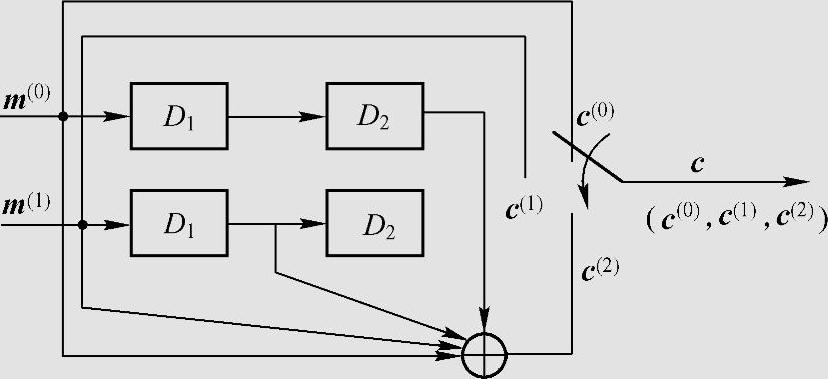
图6.16 （3，2，2）系统卷积码编码电路

由例6.56和例6.57可知，第i单元时间输入至编码器的信息组m_i及其相应的输出子码c_i，不仅与前v个子码c_i-1，c_i-2，…，c_i-v中的码元有关（例6.56中v=3，例6.57中v=2），而且也参与了后v个子码c_i+1，c_i+2，…，c_i+v中的校验运算。图6.17以（2，1，3）卷积码为例示出了卷积码的这种约束关系。从图中可见，它的每一环都与前后各环有关，这样一环扣一环就组成卷积码的一个码序列。因此，卷积码也称连环码，这种编码运算在数学上称为卷积运算。

由式（6.101）～式（6.103）（或图6.15和图6.16）可知，卷积码编码器输出的每一子码的码元，是此单元时间输入的信息子组与前v个子码中信息子组的模2加，是一种线性关系。所以，由这类编码器编出的卷积码是线性码。

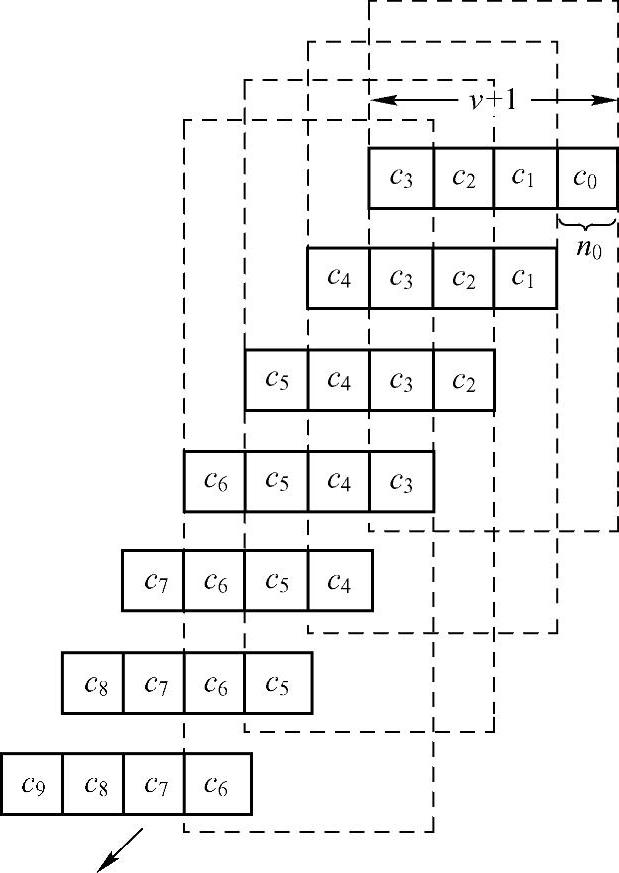
图6.17 卷积码子码之间约束关系

本书仅讨论线性卷积码，称v为编码存储，表征输入信息子组在编码器中滞留的单元时间；称v+1为编码约束度，表征编码过程中互相约束的子码个数；称（v+1）n₀为编码约束长度，表征编码过程中互相约束的码元个数。v或（v+1）n₀是表示卷积码编码器复杂性的一个重要参数。

例6.56中的卷积码，v=3，（v+1）n₀=8；例6.57中的卷积码，v=2，（v+1）n₀=9。

在卷积码的译码过程中，不仅要根据此单元时间输入到译码器的子码，而且还要根据以后很长一段时间，如v_d段单元时间内收到的各子码，才能译出一个子码的信息子组，通常v_d≥v；称v_d+1为译码约束度，称（v_d+1）n₀为译码约束长度。它们分别表征译码过程中互相约束的子码或码元个数。

在卷积码的各个子码之间，不论是编码还是译码都不是每段独立处理，而是与前后v或v_d段有关。所以，卷积码常用（n₀，k₀，v）表示。一般情况下，k₀和n₀比分组码的k和n要小，而它们的比值R=k₀/n₀称为卷积码的码率（类似于分组码码率的定义）。

卷积码的码率是衡量卷积码传输信息有效性的重要参数。

卷积码从码元结构上分为系统卷积码和非系统卷积码。若在每个子码的前k₀位为信息元，后n₀^-k0位为校验元，这样的卷积码就是系统卷积码。

例6.56的（2，1，3）码是非系统卷积码，例6.57的（3，2，2）码是系统卷积码。