1960年由R.C.Bose和D.K.Ray-Chaudhuri、1961年由A.Hocquenghern分别构造出纠正多个随机错误的码,这些码的循环结构是在1960年由W.W.Peterson证明。通常称这一类码为BCH码(以三位发现者名字的第一个字母的缩写BCH命名)。这类码是迄今为止发现的一类很好的线性纠错码,其纠错能力很强,特别在短和中等码长下,性能接近于理论限,且构造方便,编码和译码简单,特别是它具有严格的代数结构。因此,BCH码在编码理论中起着重要作用。BCH码是迄今为止研究得最为详尽,分析得最为透彻,取得的成果最多的码类之一。
RS(Reed-Solomon)码是一类有很强纠错能力的多元BCH码,是由I.S.Reed和G.Solomon于1960年构造出来的。该码在工程中得到了广泛应用。
由于BCH码性能优良,结构简单,编译码设备也不太复杂,使得它在实际使用中受到工程技术人员的欢迎,是目前用得最为广泛的码类之一。
1.BCH码的定义和构造
BCH码是纠正多个随机错误的循环码,可以用生成多项式g(x)的根来描述。
定义6.66 给定有限域GF(q)及其扩域GF(qm),其中q是素数或素数的幂,m为正整数。若GF(q)上循环码的生成多项式g(x)的根中含有δ-1个连续根αv,αv+1,…,αv+δ-2,则由g(x)生成的循环码称为q元BCH码。其中,α是GF(qm)中的n级元素,v是任意整数。
定义6.67 若BCH码生成多项式g(x)的根中,含有GF(qm)中的本原域元素,则称这种BCH码为本原BCH码;否则,称为非本原BCH码。
通常取v=0或1。若v=1,称这类BCH码为狭义BCH码。若v=0,则这一类BCH码的生成多项式g(x)必含有因式x-1,即x-1g(x)。
设mi(x)和ei分别是元素αv+i(i=0,1,…,δ-2)的最小多项式和级,则由定义6.65和定理6.39可知,BCH码的生成多项式和码长分别为
g(x)=LCM(m0(x),m1(x),…,mδ-2(x)) (6.86)
n=LCM(e0,e1,…,eδ-2) (6.87)
由式(6.75)知,BCH码的一致校验矩阵H可以写成
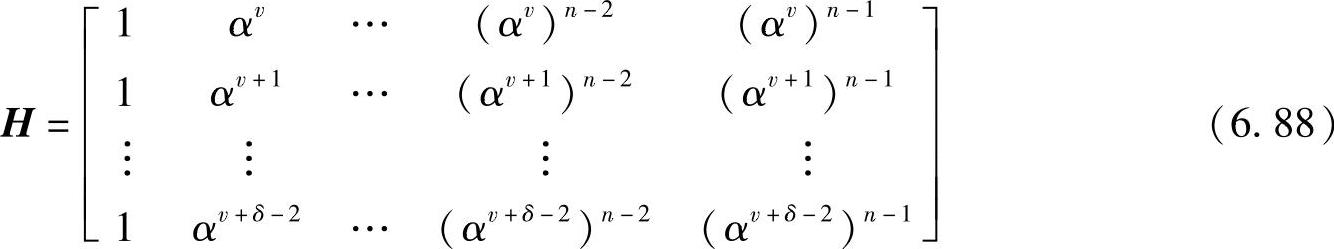
显然,本原BCH码的码长是n=qm-1,非本原BCH码的码长是qm-1的因子。
BCH码的根与最小Hamming距离有着密切关系,下面的定理给出了BCH码的距离限:
定理6.41(BCH限)BCH码的最小距离dBCH至少为δ。
定理6.41给出的BCH码的最小距离是实际最小距离的下限值,该值称为BCH码的设计距离。实际的最小距离可能大于该值。
在实际工程中,GF(2)上的二元BCH码的应用最为广泛。由BCH码的定义知,对任一个正整数m,一定可以构造出以下的二元码。
取v=1,δ=2t+1,并设α是GF(2m)中的元素,由定义6.66可知,定义在GF(2)上的二元BCH码以α,α2,…,α2t为根。又因为在特征为2的域GF(2m)上,α2i的最小多项式与αi的最小多项式相同,所以二元BCH码的生成多项式、码长和校验矩阵分别为
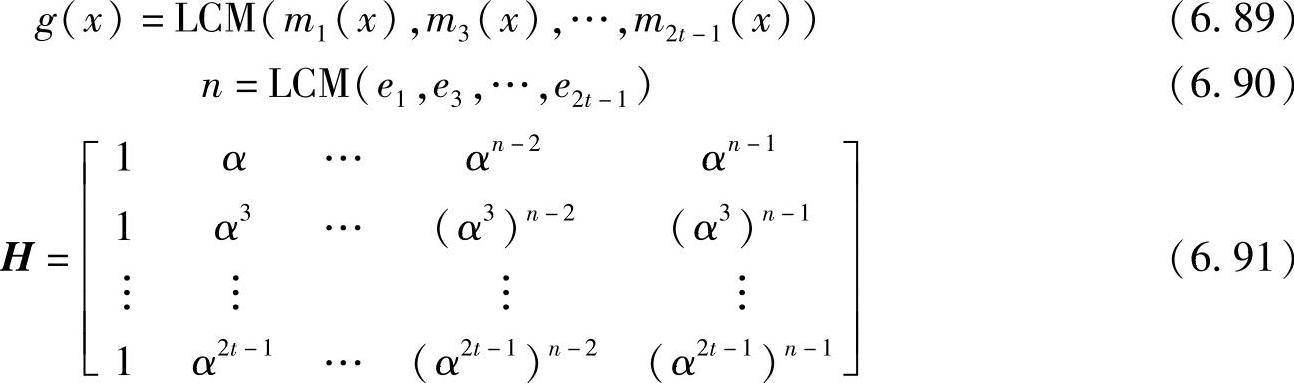
式中,mi(x)是αi(i=1,3,…,2t-1)的最小多项式,该BCH码能纠正t个错误。显然,二元BCH码的码长或者是2m-1或者是它的一个因子。上述结果归结成如下定理:
定理6.42 对任何正整数m和t,存在以α,α3,…,α2t-1为根的二元BCH码,其码长是n=2m-1或2m-1的因子,能纠正t个随机错误,校验元数目至多为mt个。
二元BCH码的具体构造步骤如下:
1)先由n=2m-1或2m-1的因子求出m值,然后寻找一个m次本原多项式m(x),构造出GF(2)的扩域GF(2m)。可以查表6.3求得本原多项式m(x)。
2)寻找GF(2m)上的一个n级元素,然后分别求出2t个连续根α,α2,…,α2t所对应的GF(2)上的最小多项式m1(x),m2(x),…,m2t(x),这可以由表6.14查表得到。
3)求出最小多项式m1(x),m2(x),…,m2t(x)的最小公倍数g(x),即可以构造相应的二元BCH码。
表6.14 二元扩域GF(2m)中连续幂次根所对应的最小多项式(m=3~8)

(续)
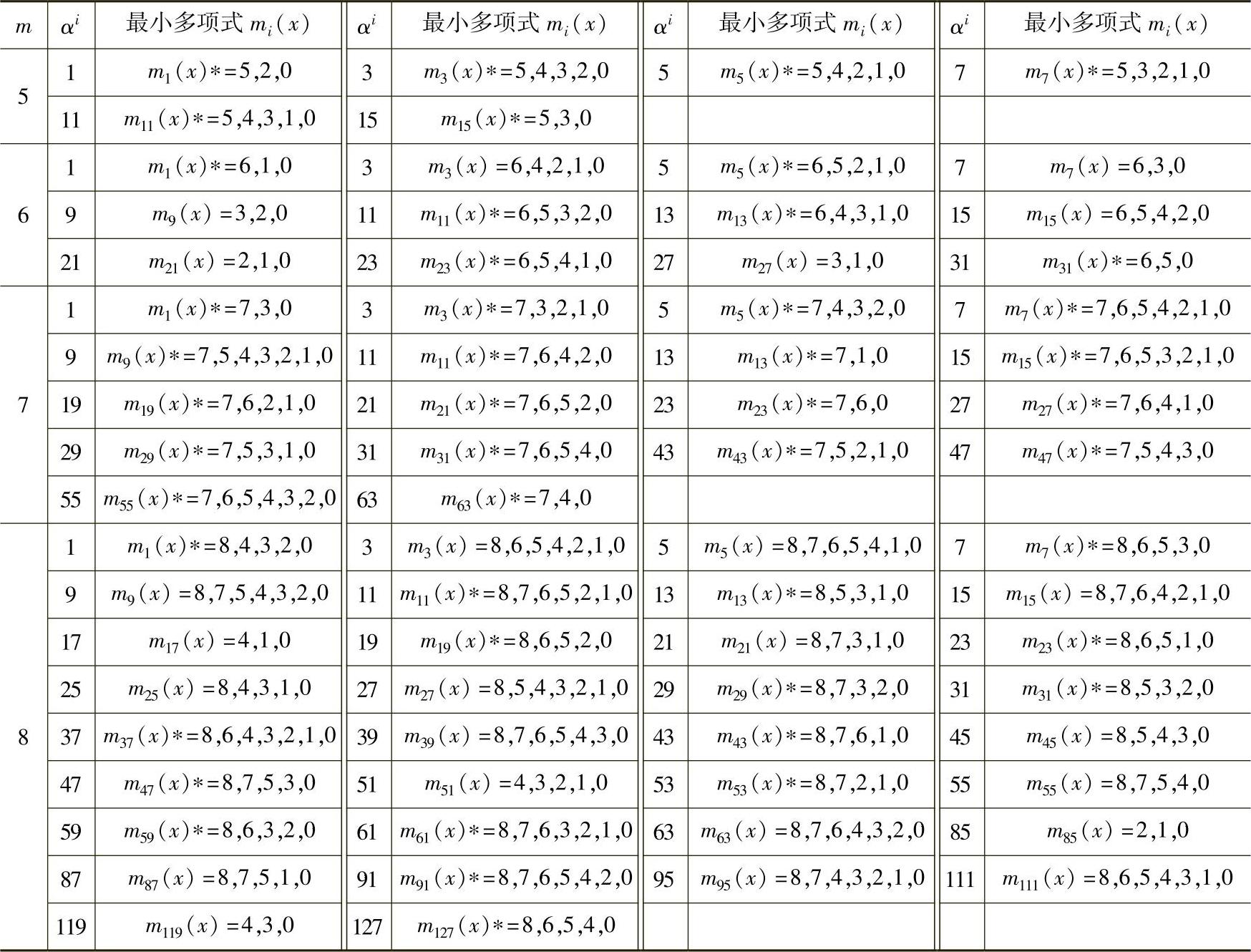
注:1.表中m(x)列的数字表示多项式非0系数所对应的幂次,如3,1,0表示x3+x+1。
2.m0(x)=x+α0=x+1是所有GF(2m)上的最小多项式,表中未列出。
3.标*号的最小多项式是本原多项式。
【例6.52】
求码长为n=24-1=15的二元BCH码。
解α∈GF(24)是本原域元素,其周期为15,且是本原多项式1+x+x4的根。
1)t=1,以α为根,α的最小多项式为m1(x)=1+x+x4,则码的生成多项式为
g(x)=m1(x)=1+x+x4校验元数目是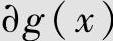 =4,得到(15,11,3)BCH码,这是纠正单个错误的循环Hamming码。由6.5.4节的定义6.63知,纠正单个错误的本原BCH码就是循环Hamming码。
=4,得到(15,11,3)BCH码,这是纠正单个错误的循环Hamming码。由6.5.4节的定义6.63知,纠正单个错误的本原BCH码就是循环Hamming码。
2)t=2,以α、α3为根,α3的最小多项式为m3(x)=1+x+x2+x3+x4,则码的生成多项式为
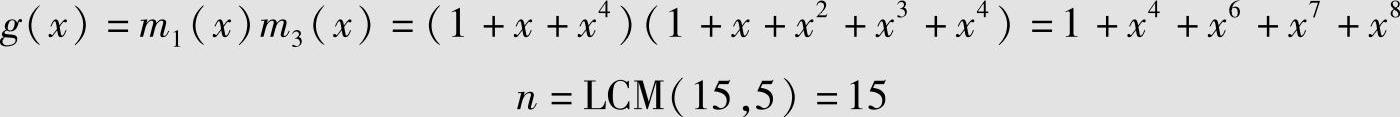
由上面的g(x)生成(15,7,5)BCH码,能纠正2个随机错误。
3)t=3,以α、α3、α5为根,α5的最小多项式为m5(x)=1+x+x2,则码的生成多项式为
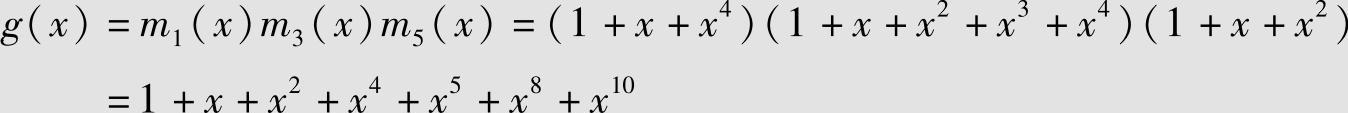
由上面的g(x)生成(15,5,7)BCH码,能纠正3个随机错误。
4)t=4,以α、α3、α5、α7为根,α7的最小多项式为m7(x)=1+x3+x4,则码的生成多项式为
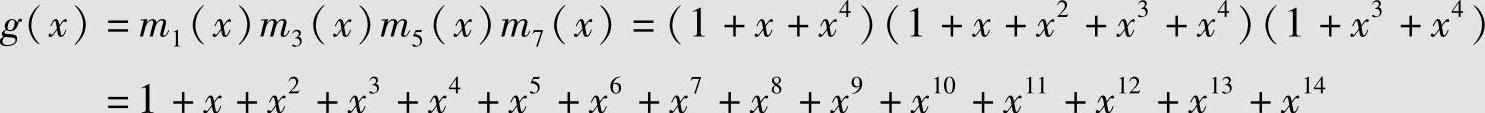
由上面的g(x)生成(15,1,15)BCH码,这是一个重复码,最小距离d=15,能纠正7个随机错误。该码虽以α、α3、α5、α7为根,但由于共轭根系的原因,该码实际上以αi(i=1,2,…,14)共14个连续元素为根,故设计距离δ=15,实际最小距离也为15。
由例6.52看出,BCH码的信息元数目、纠错个数不是连续变化,而是跳跃式变化的。上述这些码,码长n=2m-1,所以都是本原BCH码。另外,该例中的最小多项式可以利用定理6.19的方法求得,也可以用查表的方法直接得到最小多项式。
【例6.53】
求码长n=21,纠2个随机错误的BCH码。
解n=21≠2m-1,26-1=3×21,故n是26-1的因子。所以GF(26)是含有21级元素的最小域。设α是GF(26)的本原域元素,它是1+x+x6的根。令β=α3,则β是21级元素。设计以β、β3为根的BCH码,通过查表6.14得β=α3的最小多项式为m1(x)=1+x+x2+x4+x6;β3=(α3)3=α9的最小多项式为m3(x)=1+x2+x3。则码的生成多项式为
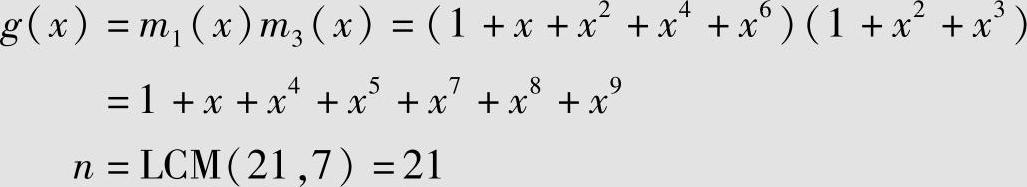
得到一个(21,12,5)非本原BCH码。
2.RS码的定义和构造
定义6.68 GF(q)(q≠2,通常q=2m)上,码长n=q-1的本原BCH码称为RS码。
显然,RS码最主要特点之一是码元取自GF(q)上,而它的生成多项式的根也在GF(q)上。所以,RS码是码元的符号域与根域相同的BCH码。因为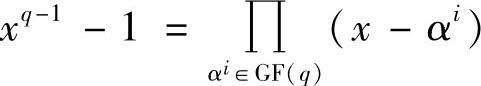 ,αi在GF(q)上的最小多项式为mi(x)=x-αi,所以,由BCH码定义可知,长为n=q-1,设计距离为δ的RS码,其生成多项式为
,αi在GF(q)上的最小多项式为mi(x)=x-αi,所以,由BCH码定义可知,长为n=q-1,设计距离为δ的RS码,其生成多项式为
g(x)=(x-αv)(x-αv+1)…(x-αv+δ-2) (6.92)
通常v=1,此时
g(x)=(x-α)(x-α2)…(x-αδ-1) (6.93)(https://www.xing528.com)
定理6.43(n,k)RS码是极大最小距离可分码,其最小Hamming距离为n-k+1。
在Singleton限意义上,RS码是最佳码。
【例6.54】
求纠正2个错误的(15,11,5)RS码的生成多项式和校验多项式。
解 n=q-1=15,故码符号取自GF(24)中的元素,设α∈GF(24)是本原域元素,它是本原多项式1+x+x4的根,GF(24)的元素表见表6.4。(15,11,5)RS码以α、α2、α3、α4为根,其生成多项式为
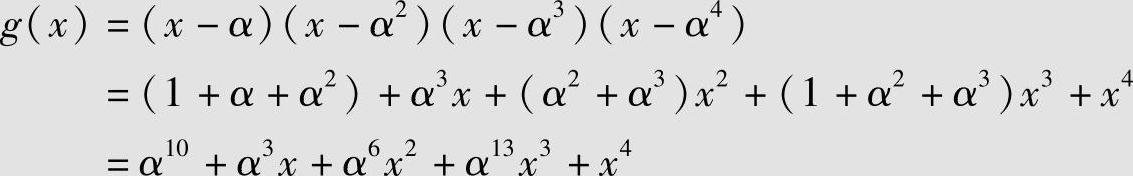
上式的g(x)生成GF(24)上的16元(15,11,5)本原BCH码,也就是(15,11,5)RS码。相应的校验多项式为
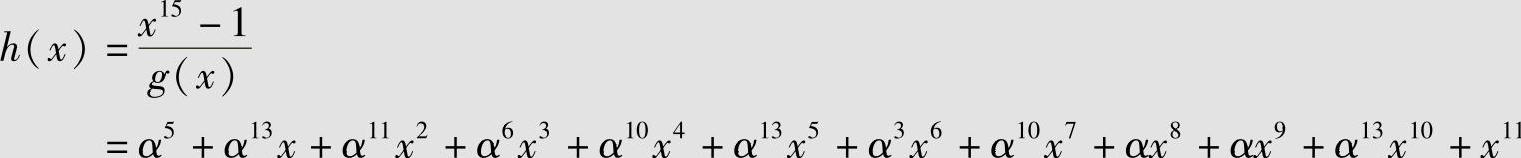
3.BCH码的译码原理
BCH码的译码与前面的线性分组码的译码步骤相同,共分为3步:
1)由接收码字r(x)计算伴随式s(x)。
2)由伴随式s(x)找出错误图样的估值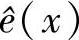 。
。
3)计算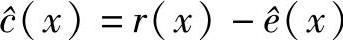 。
。
BCH码是定义在GF(qm)上的一种循环码,码元在GF(q)上取值,生成多项式的根在GF(qm)上取值。因此,这类码的译码算法一般是在GF(qm)上进行的。下面给出在GF(qm)上,BCH码的伴随式计算及其译码算法。
设α是GF(qm)中的n级元素,GF(q)上具有纠正t个错误能力的(n,k,d)BCH码的2t个连续根为α,α2,…,α2t。再设发送码字为c(x),接收码字为r(x),信道产生的错误图样为e(x),则有r(x)=c(x)+e(x)。由于α,α2,…,α2t是码的根,有c(αi)=0(i=1,2,…,2t),因此,有r(αi)=c(αi)+e(αi)=e(αi)(i=1,2,…,2t)。
由伴随式定义和式(6.91),并考虑到r(αi)=e(αi)(i=1,2,…,2t),经推导可得接收多项式的伴随式为
sk=r(αk)=e(αk),k=1,2,…,2t (6.94)
进一步设信道产生t个错误(因为码的纠错能力为t),则错误图样e(x)可以写成
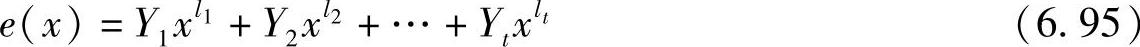
式中,Yi称为错误值,Yi∈GF(q);xli称为错误位置数,说明错误发生在r(x)中的第li位。
设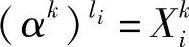 ,利用式(6.95),式(6.94)可以改写为
,利用式(6.95),式(6.94)可以改写为
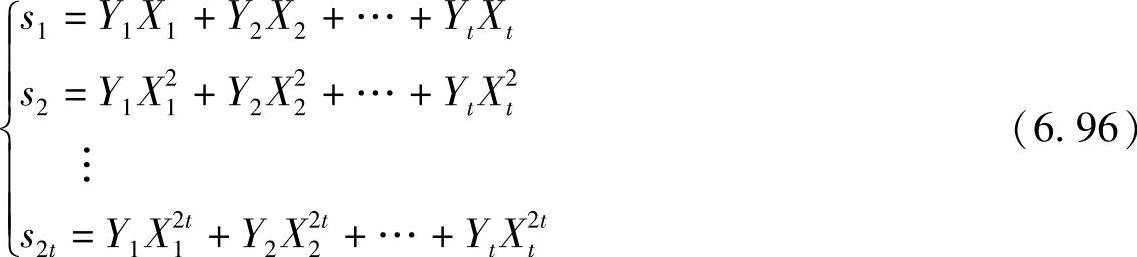
称式中的sj为Xi的加权幂和对称函数。
BCH码的译码算法就是从式(6.96)中的2t个方程中求出2t个未知数Xi和Yi(i=1,2,…,t)。但是,直接解上述方程是比较困难的,所以分两步进行。先解出错误位置数Xi,再求出错误值Yi。为此目的,引入错误位置多项式σ(x)为
σ(x)=(1-X1x)(1-X2x)…(1-Xtx)
若第k个错误位置x=Xk-1,则σ(Xk-1)=0。因此,求错误位置就是求解错误位置多项式σ(x)的根。把σ(x)展开得
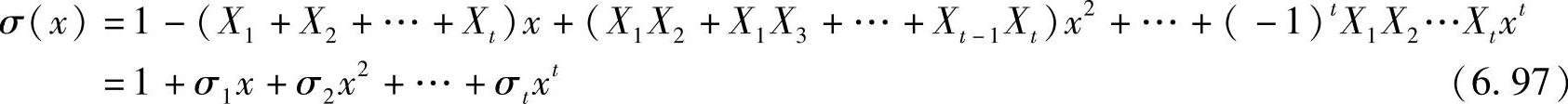
式中

称式(6.98)是Xi的初等幂和对称函数。若Xk-1为错误位置,则
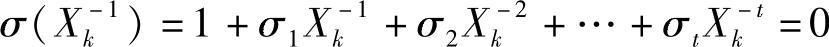
上式两边乘以Xkt(k=1,2,…,t),得

上式两边再乘以YkXjk(j=1,2,…,t),则
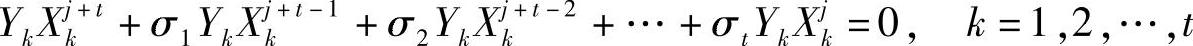
两边对k求和得
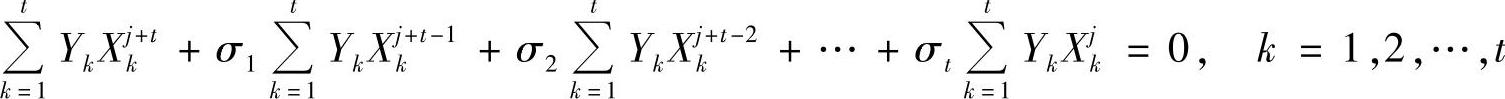
由式(6.96)知,上式可以成为
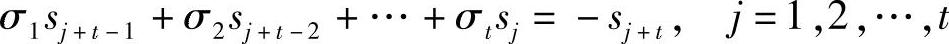
写成矩阵形式为
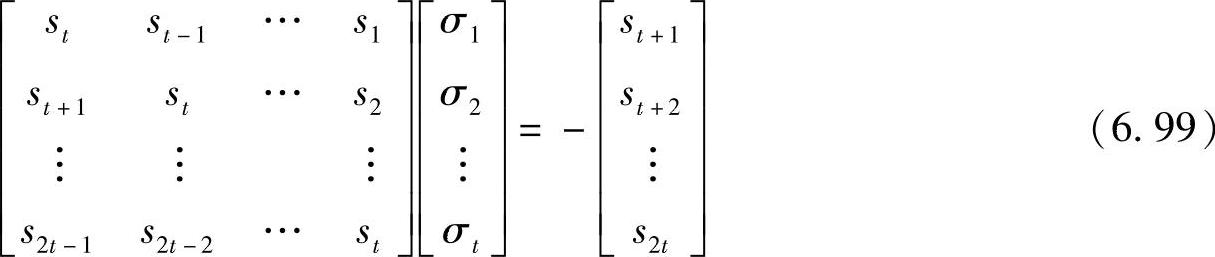
式(6.99)是一组线性方程,有t个方程和t个未知数。
方程组(6.99)有解的充要条件是t×t阶系数矩阵满秩。可以证明,若实际产生的错误个数为t,则t×t阶系数矩阵满秩;如果接收码字r(x)中只有γ<t个错误,则t×t阶系数矩阵非满秩,这就必须把t×t阶系数矩阵降至γ×γ阶满秩为止,才能求得未知数σ1,σ2,…,σγ。
求得σ(x)后解出其根,得到错误位置数X1,X2,…,Xt,并代入式(6.96)的前面t个方程中,并写成矩阵形式,得
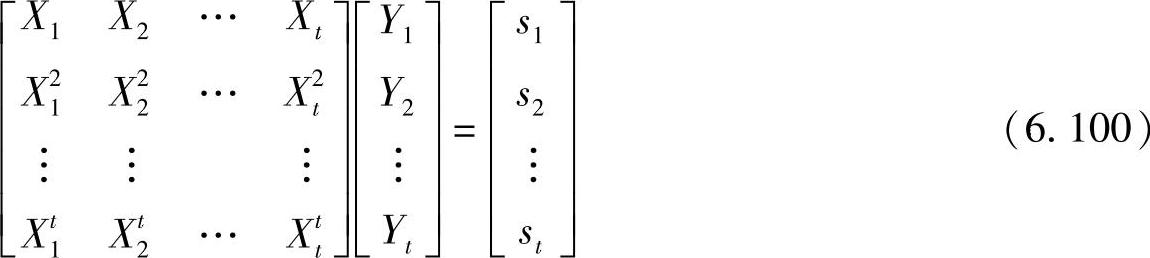
解方程组(6.100),就可以求出错误值Y1,Y2,…,Yt,从而完成译码。在二元情况下,错误值Y1,Y2,…,Yt只可能是1,故求错误值Yi这一步可以省略。
【例6.55】
二元(15,5,7)BCH码的生成多项式为g(x)=1+x+x2+x4+x5+x8+x10(见例6.52)。若接收码字为r(x)=1+x+x2+x7+x10+x13,求发送码字c(x)。
解 该码以α、α3、α5为根,α是本原多项式1+x+x4的根。根据伴随式定义式(6.96)和定理6.17中2),计算接收码字r(x)的伴随式如下:
s1=r(α)=α5,s2=r(α2)=s21=α10,s4=r(α4)=s22=α5
s3=r(α3)=α,s6=r(α6)=s23=α2,s5=r(α5)=α5
上述计算中,GF(24)的元素见表6.4。把求得的si值代入式(6.99)中,得
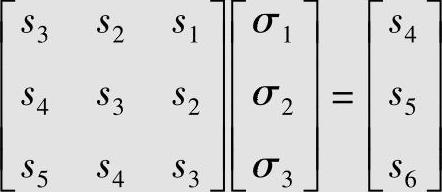
首先,检验3×3阶的系数矩阵的行列式是否为0,即计算下式:
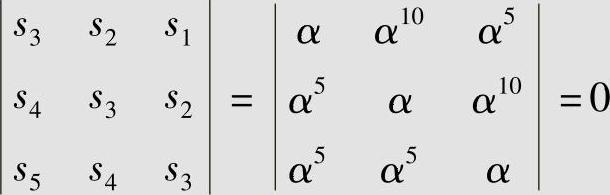
因此,实际产生的错误个数小于3,σ3=0,3×3阶系数矩阵必须降至2×2阶矩阵,得到
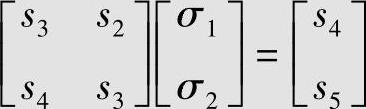
再计算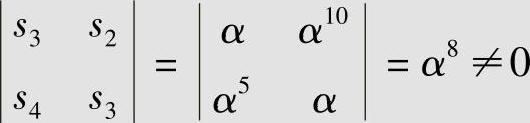 ,所以矩阵满秩,方程组有解。经计算求得σ1=α5,σ2=α14,代入错误位置多项式(6.97),可得
,所以矩阵满秩,方程组有解。经计算求得σ1=α5,σ2=α14,代入错误位置多项式(6.97),可得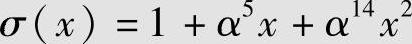 。解得σ(x)=0的2个根为α12和α4;相应的错误位置数X1=(α12)-1=α3,X2=(α4)-1=α11。由此可知,
。解得σ(x)=0的2个根为α12和α4;相应的错误位置数X1=(α12)-1=α3,X2=(α4)-1=α11。由此可知,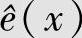
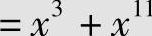 ,则发送码字为
,则发送码字为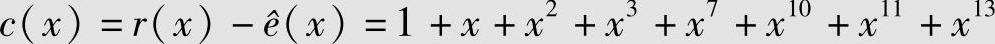 。
。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




