循环码的译码原理和电路设计

纠错码的译码器就是要对失真的接收数字信号作出正确的判断。若对接收信号作出是0或1的判断，就称其为硬判决译码。若失真信号只输出对它判定的信息，如有关它是0或1的后验概率，就是所谓的软判决译码（若不作判定，只输出一个删除符号，这是第三种判决方法）。一个纠错码的译码方法的好坏，往往决定了该码是否可用。循环码的编码理论严谨，编码电路易于实现。而且循环码有多种软、硬判决译码方法，这是它获得广泛应用的基础。通常，软判决译码比硬判决译码能多获得2～3dB的编码增益，但软判决译码设备的复杂度明显高于硬判决译码。下面讨论循环码的一般译码方法。

1.循环码的伴随式计算

循环码是线性分组码的子类，所以仍可以采用线性码的伴随式译码方法。循环码采用多项式来描述，故也可以用多项式来表述伴随式和错误图样。

设发送码字为c（x），接收码字为r（x），错误图样为e（x），即

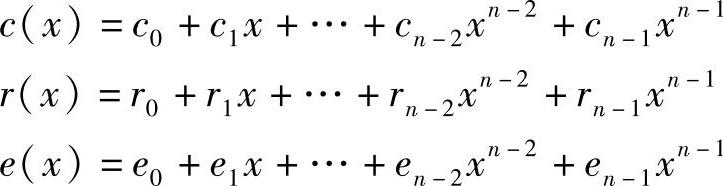
并有r（x）=c（x）+e（x）。伴随式s（x）是r（x）除以g（x）后的余式，即

式中，s（x）=s₀+s₁x+…+s_n-k-1x^n-k-1。

由于s（x）至多是n-k-1次多项式，有2^n-k种不同的表达式，e（x）至多是n-1次多项式，有2ⁿ种不同的表达式。所以，s（x）到e（x）是一对多的映射。由于译码方法的不同，选择出不同的e（x），自然不能排除选错的可能性。但仍然像线性码的译码一样，有以下三步：

1）由接收码字r（x）（用g（x）的除法电路）计算伴随式s（x）。

2）由伴随式s（x）找出错误图样的估值。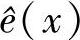

3）计算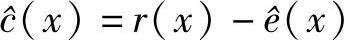。若是非系统码，还需要从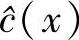中求出其信息组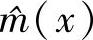。对系统码来说，省去后面一步。

上述步骤中，2）是困难的一步，要依赖于译码方法的选择，这里仅讨论译码的思想方法。首先是利用循环码的循环特点，简化伴随式的计算。

定理6.40 设s（x）是r（x）的伴随式，则r（x）的循环移位xr（x）=r（1）（x）（modxⁿ-1）的伴随式是s₁（x），那么

s₁（x）≡xs（x）（modg（x））（6.81）

证明 由伴随式定义式（6.80），s（x）≡r（x）（modg（x）），由同余式的性质有

xs（x）≡xr（x）（modg（x）） （6.82）

因为xⁿ-1=g（x）h（x），设r₁（x）≡xr（x）（modxⁿ-1），则该式可以写成

r₁（x）≡xr（x）（modg（x）） （6.83）

在s₁（x）≡r₁（x）（modg（x））中，把式（6.83）代入，并由式（6.82），有

r₁（x）≡xr（x）（modg（x））≡xs（x）（modg（x））

【证毕】

由定理6.40可以推得，xⁱr（x）的伴随式为s_i（x）≡xⁱs（x）（modg（x））（i=0，1，…，n-1）。

伴随式计算电路的这些性质，在循环码的译码运算中非常有用。

若c（x）是循环码C的码字，则xc（x）∈C。因此，若s（x）≡e（x）（modg（x））是r（x）=c（x）+e（x）的伴随式，则xs（x）≡xe（x）（modg（x））就是xr（x）=xc（x）+xe（x）的伴随式。也就是说，若e（x）是可以纠正的错误图样（陪集首），则e（x）的循环移位xe（x）也是可以纠正的错误图样。一般说来，xⁱe（x）（i=1，2，…，n-1）也是可以纠正的错误图样。

为此，根据这种循环关系划分错误图样，把特定的错误图样及其所有循环移位作为一类。如将错误图样（100…0），（010…0），…，（00…01）作为一类，并以首位为非0的错误图样（100…0）作为此类图样的代表。在q元时，若码要纠正≤t个错误，则错误图样类的种数为

(www.xing528.com)

译码时，只要知道此类错误图样的伴随式，该类中其他错误图样的伴随式都可以由此类图样的伴随式通过伴随式电路运算得到。这样就简化了循环码译码器的错误图样识别电路，由原来识别

个图样减少到N₁个。例如，在二元码时，若n=63，t=1～5，由式（6.84）和式（6.85）计算译码器所需识别的错误图样个数见表6.12。

表6.12 N₁、N₂比较表

纠错码译码设备的复杂性主要取决于由伴随式找出错误图样的识别电路或组合逻辑电路的复杂性。由表6.12可知，虽然循环码识别错误图样的个数比非循环码大为减少，但随着n和t的增加快速增长，以至难以实现。因此，利用组合逻辑电路识别错误图样类的方法仅适用于n和t较小的情况。若n和t都较大，则必须利用循环码的其他特性寻找更为简单和巧妙的译码方法，这是纠错编码理论和应用中最引人注目的研究课题之一。

2.循环码的通用译码器

循环码的伴随式计算可以用除法电路实现，该电路的复杂性正比于一致校验元的数目（即n-k）。对于二元码，纠正错误这一步是把错误图样与接收码字简单地进行模2加即可。若以串行方式（即一次一位）实现纠错，则用单个异或门就能做到。借助译码表，可以由伴随式完全确定错误图样。

设计译码电路的简单方法是用组合逻辑电路，在译码表中由伴随式寻找错误图样。然而，此方法的局限性是译码电路的复杂度随码长和纠错数目的增加呈指数率增长。循环码有很多代数和几何特性，如果能充分利用这些特性，就有可能简化译码电路。

图6.13给出了（n，k，d）系统循环码的通用译码器框图。它由伴随式计算电路、错误图样检测器和r（x）缓冲寄存器三个主要部分组成。接收码字r（x）从左端移入伴随式计算电路。只要简单地把一个错误数据由左端通过异或门供给移位寄存器，就可以消除错误数据对伴随式的影响。译码算法描述如下：

1）门通，k个移位脉冲将接收码字r（x）的前k位信息元存入k级缓冲寄存器，等待纠错；同时，也将这k位信息组移入伴随式计算电路。

2）门断，k级缓冲寄存器停止移位；再用n-k个移位脉冲将接收码字r（x）余下的n-k位校验元移入伴随式计算电路得到伴随式。

3）把伴随式读入E_n-1图样检测器，以探测相应的错误图样。E_n-1检测器是组合逻辑电路，其功能是：当且仅当伴随式计算电路中的伴随式与在最高位x^n-1有错的错误图样相对应时，它才输出1。即若检测器的输出是1，则在缓冲寄存器最右边一级的接收符号有错误时，需要纠正；否则，不必纠正。

4）由缓冲寄存器读出第一个接收符号，同时伴随式寄存器移位1次。若检测到第1个接收符号有错误，则用检测器的输出予以纠正，且检测器的输出反馈到伴随式计算电路以修正伴随式（即消除错误符号对伴随式的影响）。这样便得到了一个新的伴随式，它相应于向右移位1次后所得的修正接收码字的伴随式。

5）由第3）步得到的新伴随式，用来检测第2个接收符号（现在它在缓冲寄存器的最右边1级）是否有错。译码器重复第3）和4）步。第2个接收符号的纠正方法与第1个接收符号相同。

6）译码器逐个符号地译接收码字，共进行n次，完成全部接收码字的译码。

上述译码器就是著名的Meggitt译码器，原则上它可以用于任何循环码的译码。但是，它能否在实际中得到应用，完全取决于错误图样检测电路的复杂度。该译码器需要用2n个移位脉冲实现一次循环码的译码。

【例6.51】

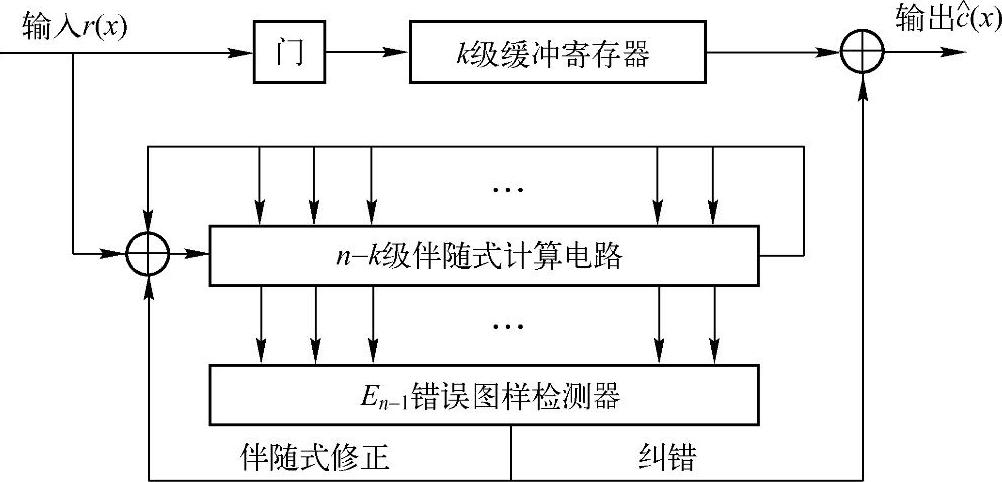
图6.13 循环码通用译码器

二元（7，4，3）循环Hamming码生成多项式为g（x）=1+x+x³，该码的最小距离为3，能纠正7长接收码字中的任何单个错误。图6.14是其译码电路图。接收码字为r（x）=x+x²+x³+x⁴+x⁶，即r=（0111101），表6.13是其译码过程。

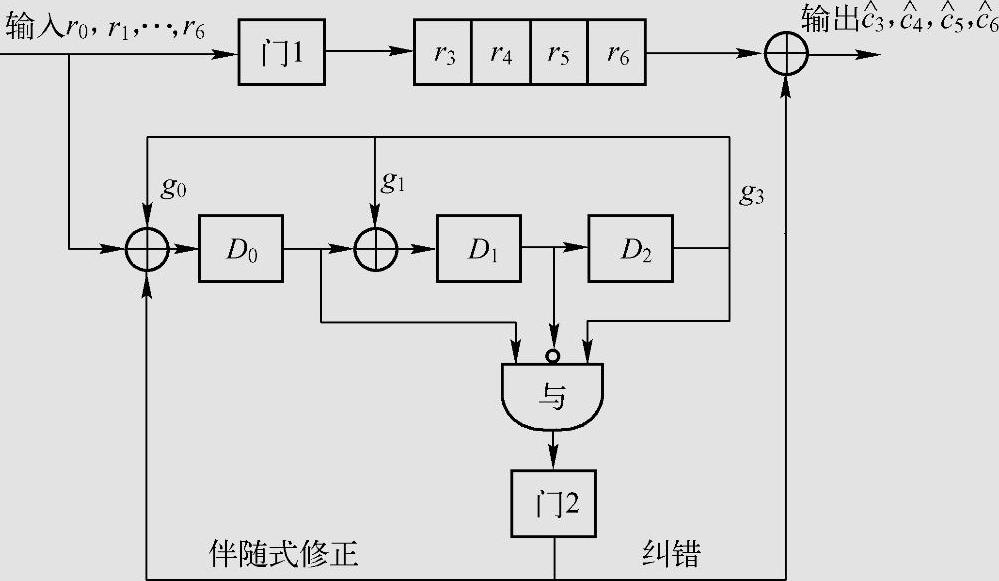
图6.14 （7，4，3）循环码译码器

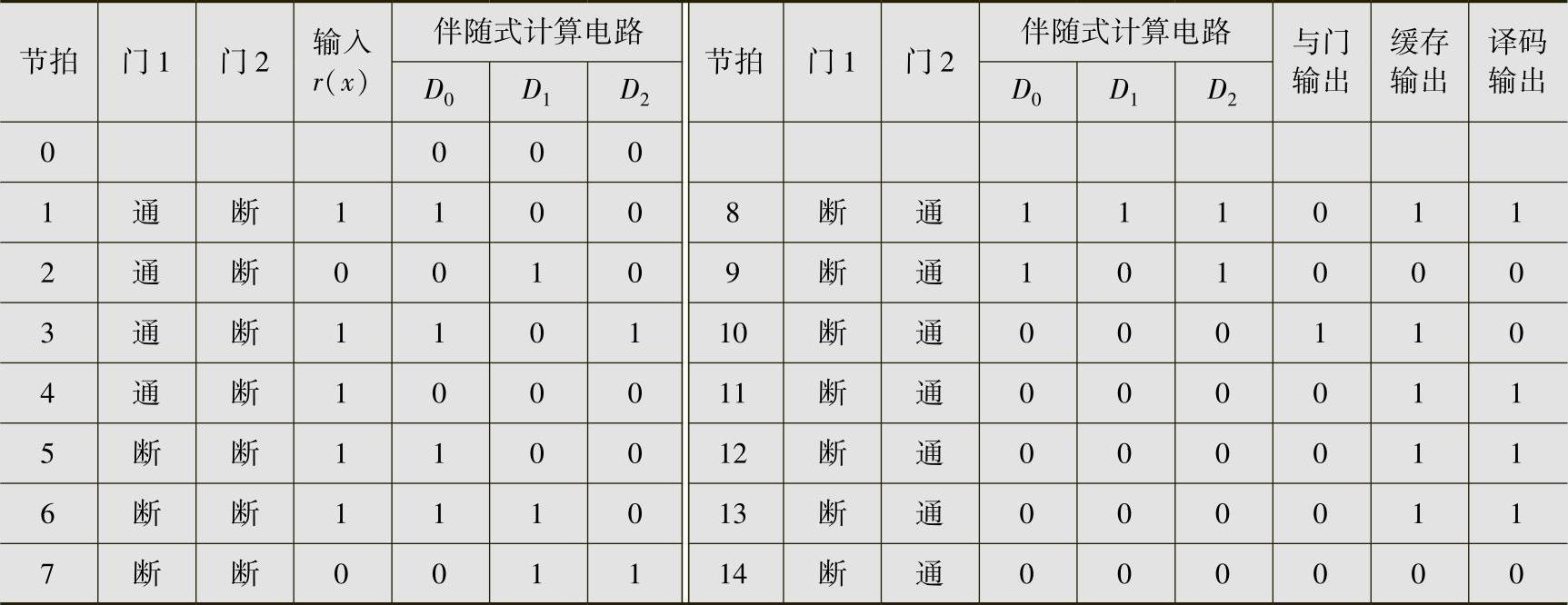
表6.13 图6.14的（7，4，3）循环码译码过程

缩短循环码的译码方法可以在原码译码器的基础上作适当修改即可。