循环码编码电路的实现

（n，k，d）循环码由次数为n-k次的生成多项式g（x）或由次数为k次的一致校验多项式h（x）完全描述。因此，（n，k，d）循环码的编码电路可以分别由g（x）或h（x）确定，主要有两种。其中，由g（x）确定的编码电路称为n-k级编码器，由h（x）确定的编码电路称为k级编码器。

1.n-k级编码器

n-k级编码器有两种实现形式，一种是g（x）的乘法电路，该编码器产生非系统码；另一种是g（x）的除法电路，该编码器产生系统码。

（1）g（x）乘法电路编码器

（n，k，d）循环码的编码是将k长信息多项式m（x）=m₀+m₁x+…+m_k-1x^k-1编成n长码字c（x）。由循环码理论知，c（x）=m（x）g（x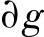）（（x）=n-k）。因此，非系统循环码可以用n-k级g（x）乘法电路实现编码。图6.7是这种编码电路的通用结构，工作过程如下：

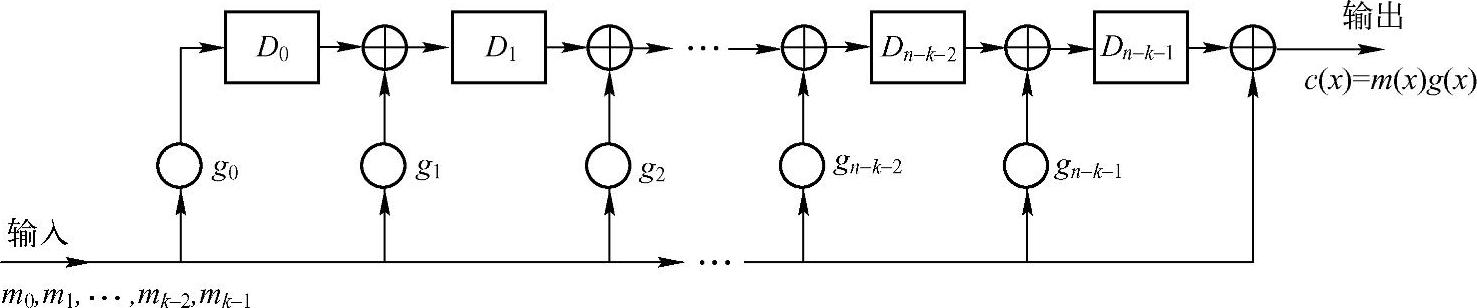
图6.7 （n，k，d）循环码n-k级乘法编码器

1）n-k级移位寄存器的初始状态清0，送入信息组m（x）的系数，高次位系数先进入电路。

2）经k次移位后，m（x）全部送入电路。

3）将输入置0，再经过n-k次移位后，编码器输出完整码字。

（n-l，k-l）缩短循环码的编码电路与（n，k，d）循环码的编码电路相同。但工作过程修正为在第2）步的运算时，用k-l次移位将m（x）送入电路即可，编码过程用k-l次节拍完成。

【例6.48】

二元（7，4，3）循环Hamming码生成多项式为g（x）=1+x+x³。图6.8是该码的n-k=3级乘法编码器。设送入的信息组为1001，相应的信息多项式为m（x）=1+x³，则编出的码字是1100101，相应的码多项式为1+x+x⁴+x⁶。

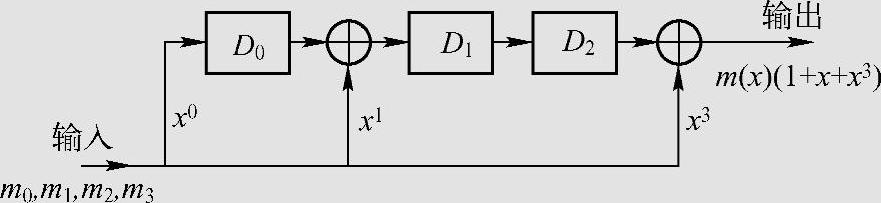
图6.8 （7，4，3）循环码3级乘法编码器

（2）g（x）除法电路编码器

6.5.2节中给出系统形式循环码编码算法的3个步骤：①计算m（x）乘以-x^n-k得到-x^n-km（x）；②用g（x）除-x^n-km（x）得到相应的余式r（x）；③系统码的码字为c（x）=x^n-km（x）+r（x）。所以，（n，k，d）系统循环码的编码电路就是乘-x^n-k除g（x）的电路，其编码电路的一般形式如图6.9所示。这种编码电路的工作过程如下：

图6.9 （n，k，d）循环码n-k级除法编码器

1）n-k级移位寄存器的初始状态清0，门1通、门2断，然后进行移位，送入信息组m（x）的系数，高次位系数首先进入电路，它一方面经或门输出，一方面自动乘以-x^n-k后进入g（x）除法电路，从而完成了-x^n-km（x）的运算。

2）经k次移位后，m（x）全部送入电路，完成了除法运算，此时在移位寄存器内保留了余式r（x）的系数，在二元情况下就是校验元。

3）此时门1断、门2通，再经过n-k次移位后，把移位寄存器的n-k位校验元经取逆运算后全部输出，与原先的k位信息组组成n长的码字c（x）。对于二元码则不需取逆运算。

4）门1通、门2断，送入第2组信息组，并重复上述过程。

（n-l，k-l）缩短循环码的n-k级编码电路与（n，k，d）循环码的编码电路相同。但工作过程修正为在第2）步的运算时，用k-l次移位将m（x）送入电路即可，编码过程用n-l次节拍完成。

【例6.49】(www.xing528.com)

二元（7，4，3）循环Hamming码的生成多项式为g（x）=1+x+x³。图6.10是该码的n-k级除法编码电路。设输入消息多项式为m（x）=1+x³，即m=（1001）。表6.10给出该编码器的编码过程，7次移位后输出端的码字是0111001，相应的码多项式为x+x²+x³+x⁶。

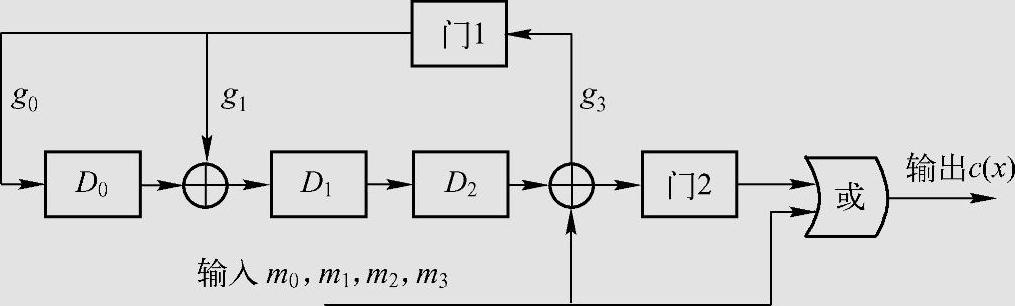
图6.10 （7，4，3）循环码3级除法编码器

表6.10 图6.10电路的编码过程

2.k级编码器

循环码的编码也可以用它的一致校验多项式h（x）=h₀+h₁x+…+h_k-1x^k-1+h_kx^k来实现。令c=（c₀，c₁，…，c_n-2，c_n-1）是一个码字，6.5.3节已证明c的分量满足式（6.67）的n-k个方程。因为h_k=1，故式（6.67）可以改写成如下形式：

对于系统循环码来说，每一码字的c_n-k，c_n-k+1，…，c_n-1分量是信息元。给定这k个信息元，利用式（6.79）的差分方程可以决定n-k个一致校验元c₀，c₁，…，c_n-k-1。基于式（6.79）的编码电路是k级编码器。其编码电路的一般形式如图6.11所示，图中的反馈连线由一致校验多项式h（x）的系数决定。注意h_k=1，h₀≠0；对于二元码，h₀=1。k级编码器的编码过程如下：

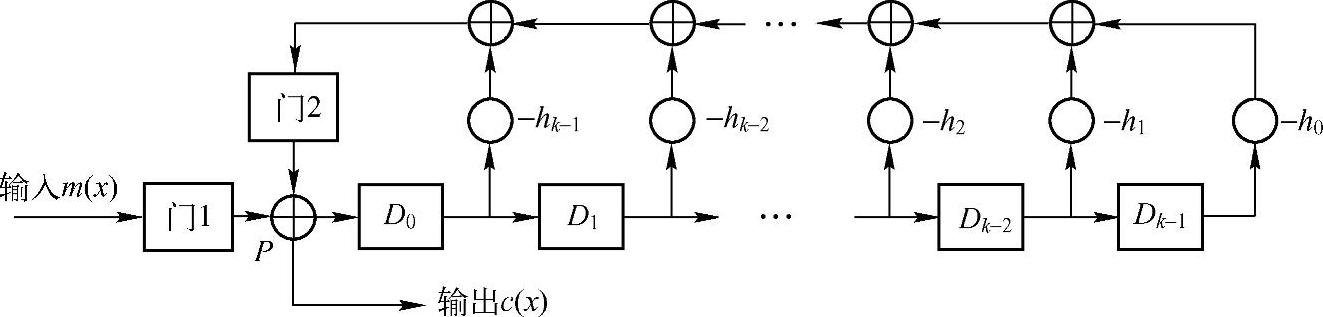
图6.11 （n，k，d）循环码k级编码器

1）开始工作时，门1通，门2断；用k个移位脉冲将k个信息元m（x）=m₀+m₁x+…+m_k-1x^k-1从高次位到低次位依次送入移位寄存器和通信信道。

2）k次移位后，门1断，门2通，在P点形成第1个一致校验元c_n-k-1。

3）移位寄存器移位1次。第1个一致校验元c_n-k-1被送入信道，并同时送入移存器；在P点形成第2个一致校验元c_n-k-2。

4）反复进行第3）步，直到n-k个一致校验元全部生成并送入信道为止。

5）门1通、门2断，送入第2组信息组重复上述过程。

（n-l，k-l）缩短循环码的k级编码电路与原（n，k，d）循环码的k级编码电路相同。但工作过程修正为在第1）步的运算时，用k-l次移位将m（x）送入电路即可，编码过程用n-l次节拍完成。

比较本节中介绍的两个编码电路可以得出如下结论：对于校验元多于信息元的循环码，k级编码器较为经济；否则，n-k级编码器要好些。

【例6.50】

二元（7，4，3）循环Hamming码生成多项式为g（x）=1+x+x³，其校验多项式h（x）为h（x）=（x⁷-1）/g（x）=1+x+x²+x⁴。图6.12是该码的k级编码电路。设输入信息多项式为m（x）=1+x³，即m=（1001）。表6.11给出该编码器的编码过程，7次移位后输出端得到码字x+x²+x³+x⁶。可见编码结果与例6.49相同。

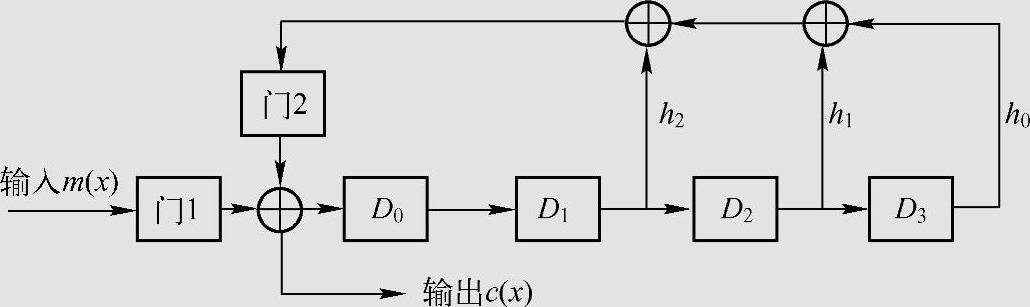
图6.12 （7，4，3）循环码4级编码器

表6.11 图6.12电路的编码过程