用多项式的根定义循环码

循环码的每个码多项式都是g（x）的倍式，g（x）的根也是所有码多项式的根。因此，可以用多项式的根来描述循环码。

设GF（q）上循环码的生成多项式为

g（x）=g₀+g₁x+…+g_r-1x^r-1+x^r，g_i∈GF（x），i=0，1，…，r-1且g₀≠0

它必在某一个GF（q）的扩域上完全分解，即它的全部根必在此扩域上。

关于g（x）的根可以分为无重根和有重根两种情况。由于有重根情况下用g（x）生成的码，比无重根时生成的码，除个别码外通常要差，故下面仅讨论g（x）无重根的情况。

由于g（x）xⁿ-1，或g（x）h（x）=xⁿ-1，若g（x）有n_i个重根，则xⁿ-1也必含有这n_i个重根。因此，要保证g（x）无重根，首先必须要求xⁿ-1无重根。

定理6.38 GF（q）上，当且仅当n与q互素时多项式xⁿ-1无重根，其中n＞q。

由定理6.38易知，在GF（2）上g（x）无重根的条件是n为奇数。因此，在二元循环码中，码长n通常是奇数。

下面讨论在无重根的条件下，用g（x）的根定义的循环码。

在GF（q）的扩域GF（q^m）上，设g（x）有r个互不相同的根α₁，α₂，…，α_r（α_i≠α_j，i≠j）。则g（x）可以写成

g（x）=（x-α₁）（x-α₂）…（x-α_r） （6.73）由于g（x）生成的循环码的每个码多项式是g（x）的倍式，因此，这些码多项式c（x）也必以α₁，α2，…，α_r为根。设码多项式为c（x）=c₀+c₁x+…+c_n-2x^n-2+c_n-1x^n-1，则有

c（α_i）=c₀+c₁α_i+…+c_n-2αⁿ_i-2+c_n-1αⁿ_i-1=0，i=1，2，…，r （6.74）

写成矩阵形式为

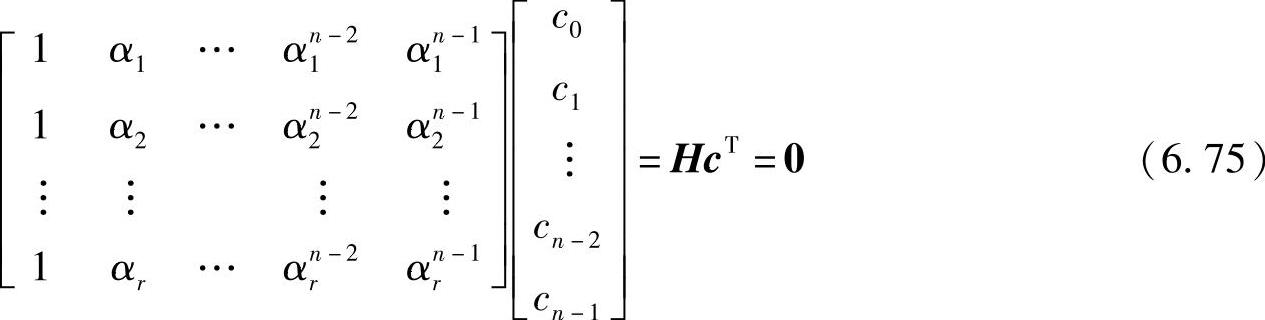
所以循环码的一致校验矩阵H又可以写成(www.xing528.com)

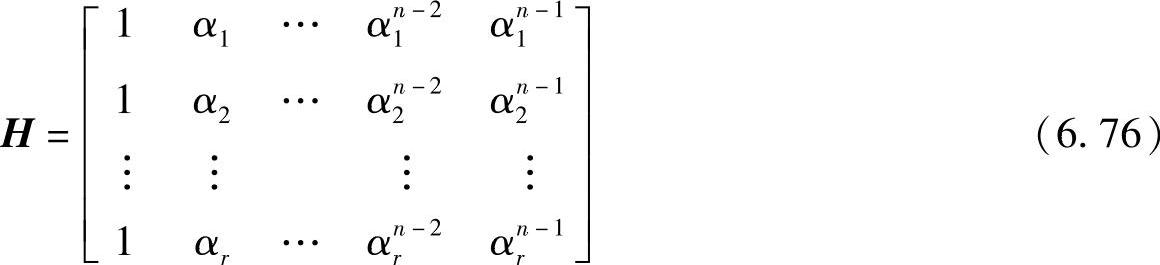
式（6.76）说明，若码多项式c（x）以α₁，α₂，…，α_r为根，则它必在式（6.76）的矩阵H的零空间中。

若α_i的最小多项式为m_i（x）（i=1，2，…，r），则只有g（x）和c（x）同时能被m₁（x），m₂（x），…，m_r（x）除尽时，g（x）和c（x）才能以α₁，α₂，…，α_r为根。为此，给出下面定义：

定义6.65 设α₁，α₂，…，α_r∈GF（q^m），m_i（x）是α_i的最小多项式，则生成多项式定义为

g（x）=LCM（m₁（x），m₂（x），…，m_r（x））（6.77）

定理6.39 以α₁，α₂，…，α_r为根的循环码的码长n为

n=LCM（e₁，e₂，…，e_r）（6.78）

式中，e_i是α_i元素的级，i=1，2，…，r。

由于α_i∈GF（q^m），由有限域理论知，该域中的每个元素由q^m-1级元素（本原元）α的幂生成；若令α_i=αⁱ，且它的最小多项式为m_i（x），则由定理6.17中4）可知，α^q_i=α^iq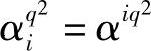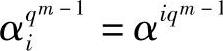，，…，也是m_i（x）的根。因此，g（x）仅含有共轭根系的最小多项式作为其中的一个因子。

求g（x）的关键是找出每个根的最小多项式。但是，当GF（q^m）很大时，计算就很复杂，因此，一般用查表的方法直接得到最小多项式。后面的表6.14给出了GF（2^m）（m=3～8）上的最小多项式。从表中可见m=3～8次的本原多项式的个数分别为2、2、6、6、18、16。

【例6.47】

求GF（2⁴）上以α、α²、α⁴、α⁸为根的循环码。设α∈GF（2⁴）是本原域元素，则α、α²、α⁴、α⁸是它的共扼根系，由表6.3得它的最小多项式（本原多项式）m₁（x）=1+x+x⁴。因此，以α、α²、α⁴、α⁸为根的循环码的生成多项式为g（x）=m₁（x）=1+x+x⁴，码长n就是α的级数，等于2⁴-1=15，故得到一个（15，11）循环码，这是一个循环Ham-ming码。该码的校验矩阵为

码多项式c（x）的系数在基域GF（2）上，它的根α、α²、α⁴、α⁸在扩域GF（2⁴）上，而GF（2⁴）上的元素都可以用GF（2）上的4维矢量表示。因此，若将矩阵H化成GF（2）上的元素，则共有16行，而其中只有4行线性无关。