循环码的一致校验多项式和校验矩阵优化

定理6.36指出，（n，k，d）循环码C的生成多项式g（x）是xⁿ-1的因式，因此有

xⁿ_-1=g（x）h（x） （6.64）

因为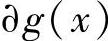=n-k，g_n-k=1，g₀≠0，所以，h（x）是如下形式的k次多项式：

下面证明（n，k，d）循环码C的一致校验矩阵可以由h（x）得到。

令c=（c₀，c₁，…，c_n-2，c_n-1）是C中的任一码字，由定理6.34知c（x）=a（x）g（x）。用h（x）乘c（x），并注意到式（6.64），可得

c（x）h（x）=xⁿa（x）-a（x） （6.66）

由于，故在xⁿa（x）-a（x）中不会出现x^k，x^k+1，…，x^n-1等各次幂项。若把式（6.66）左边的乘积c（x）h（x）展开，则x^k，x^k+1，…，x^n-1项的系数必为0。因此，得到以下n-k个方程：

根据互反多项式的定义6.33，h（x）的互反多项式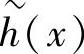为

容易看出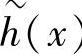，亦是xⁿ-1的一个因式。多项式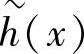生成（n，n-k）循环码，它有如下形式的（n-k）×n阶矩阵作为它的生成矩阵：

由式（6.67）的n-k个方程可知，C中的任何一个码字c与式（6.69）定义的矩阵H的每一行正交。因此，H是循环码C的一致校验矩阵，且H的行空间是C的对偶码。由于一致校验矩阵H是通过多项式h（x）得到的，为此给出定义：

定义6.62 设h（x）=（xⁿ-1）/g（x），称h（x）为（n，k，d）循环码的校验多项式；其中g（x）是该码的生成多项式。

显然，循环码也可以由它的校验多项式h（x）唯一地确定。在上述推导过程中，除了得到循环码的一致校验矩阵以外，还证明了如下定理所述的另一重要特性。(www.xing528.com)

定理6.37 令C是生成多项式为g（x）的（n，k，d）循环码，则它的对偶码也是循环的，且由多项式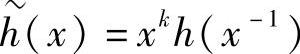生成。

【例6.45】

二元（7，4，3）循环码的生成多项式为g（x）=1+x²+x³，则

故有，可以验证如下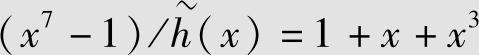：。生成的（7，3，4）循环码。该码是由g（x）=1+x²+x³生成的（7，4，3）循环码的对偶码。

对于系统形式的（n，k，d）循环码C，式（6.62）给出了其形如G=[PI_k]的生成矩阵。根据关系式GH^T=0，可以得到相应的一致校验矩阵H为

式中，H矩阵的后k列-r^T_i（x）（i=0，1，…，k-1）表示由r_i（x）的系数组成的列矢量，其中r_i（x）由式（6.60）确定；H矩阵的前n-k列是x⁰，x¹，…，x^n-k-1的系数，由于它们的次数小于n-k，所以它们被g（x）取模以后不变。因此，式（6.70）写成

对于（n-l，k-l）缩短循环码，依据定义6.60和式（6.71），不难得到其一致校验矩阵为

式（6.62）和式（6.71）就是循环码的系统码形式的生成矩阵G和校验矩阵H的一般表示式。

【例6.46】（续例6.44）

二元（7，4，3）循环码的生成多项式为g（x）=1+x²+x³。在例6.44中已计算r₀（x）≡-x³≡1+x（mod g（x）），r₁（x）≡-x⁴≡x+x²（mod g（x）），r₂（x）≡-x⁵≡1+x+x²（mod g（x）），r₃（x）≡-x⁶≡1+x²（mod g（x）），由式（6.71）知，该码的系统码形式的校验矩阵为

该码缩短两位得到（5，2）缩短循环码，由式（6.72）知，其一致校验矩阵为