信息论构造新码的方法，由已知码出发

由一个已知码构造新码的方法可以从原码的码字集合来讨论。对于线性码来说，也可以从原码的生成矩阵G或一致校验矩阵H来讨论，即对原码的G或H进行适当修正和组合，以构造新码。这些方法虽然很简单，但很实用，且是构造各种复合码的基础。

6.4.3节给出的对偶码是由线性分组码构造（n，n-k）线性分组码的一个实例。此外，属于这类方法构造的码主要还有扩展码、删余码、增广码（增信删余码）、增余删信码、缩短码和延长码等。

定义6.53 设C是二元（n，k，d）线性分组码，若对每一个码字c=（c₀，c₁，…，c_n-1）增加一个校验元c′₀，满足以下校验关系：

c′₀+c₀+c₁+…+c_n-1=0 （6.46）

则称新构造的（n+1，k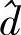，）线性分组码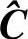为原码的扩展码，称c′₀为全校验元。

若原线性分组码C的校验矩阵为H，则不难得到扩展码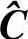的校验矩阵为

可以证明，若原码的最小Hamming距离d为奇数，则扩展码的最小Hamming距离。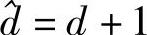

（2^m-1，2^m-1-m，3）Hamming码的扩展码是（2^m，2^m-1-m，4）码，它的中的一致校验矩阵H是Hamming码的校验矩阵。

定义6.54 将二元（n，k，d）线性分组码C删去一个校验元得到（n-1，k，d^*）线性分组码C^*，称C^*为原码C的删余码。

由定义知，删余码由扩展码的逆过程得到，它在原（n，k，d）码C的基础上，删去一个校验元构成。C^*码的最小Hamming距离d^*可能比原码小1，也可能不变。

【例6.35】（续例6.34）

在例6.34的二元（7，4，3）Hamming码上，附加一个全校验元c′₀后，得到二元（8，4，

4）扩展Hamming码，其校验矩阵由式（6.47）得

反过来，将（8，4，4）扩展Hamming码，删去校验元c′₀后，得到（7，4，3）Hamming码。

定义6.55 设二元（n，k，d）线性分组码C没有全1码字，在它的G矩阵上增加一组全1行得到生成矩阵G_a，称由G_a定义的（n，k+1，d_a）线性分组码C_a为增广码（或增信删余码）。

由定义可见，增广码C_a是在原码C的基础上，增加一个信息元，删去一个校验元得到的。增广码的生成矩阵为

与增广码构造过程相反的码是增余删信码。

定义6.56 设二元（n，k，d）线性分组码C的最小Hamming距离d为奇数，则其全体偶数重量的码字组成一个新（n，k-1，d′）码C′，称C′为原码C的增余删信码。

可以证明，若原码的最小Hamming距离d为奇数，则增余删信码的最小Hamming距离d′=d+1。

【例6.36】（续例6.29）(www.xing528.com)

如例6.29中的二元（7，3，4）线性分组码对它进行增广，得到二元（7，4，3）Hamming码，它的生成矩阵由式（6.48）得到

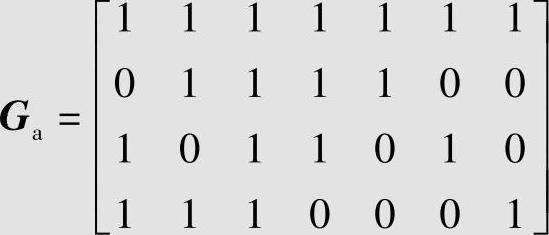
由生成矩阵G_a生成的二元（7，4，3）Hamming码的16个码字为

0000000，0111100，1011010，1100110，1110001，1001101，0101011，0010111

1111111，1000011，0100101，0011001，0001110，0110010，1010100，1101000

反过来，在上面的二元（7，4，3）Hamming码的16个码字中选出全部重量为4的码字，便得到二元（7，3，4）增余删信码。

定义6.57 对于（n，k）线性分组码C，选出最高位码元c_n-1=0的全体码字，并去掉这一位得到一个n-1长的新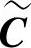码，称码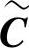为原码C的缩短码。

反复应用缩短码的方法缩短线性分组码，便得到（n-i，k-i）缩短线性分组码。

定理6.30 （n，k，d）线性分组码缩短i位后，得到的码是（n-i，k-i）线性分组码，其最小Hamming距离至少为d。

证明 因为缩短码的全部码字是由原码中对应缩短的码元位为0元的码字组成，所以，对于缩短码而言，并没有改变码元之间的线性约束关系。因此，缩短码是线性码。

又因为当把对应于缩短的码元补上0元后，缩短的每个码字便成为原码中的一个码字，所以缩短码的最小Hamming重量不会小于原码的最小Hamming重量d。因此，由定理6.23知，（n-i，k-i）缩短码的最小Hamming距离至少为d。

【证毕】

（n-i，k-i）缩短码是（n，k）线性分组码缩短i位得到的，因而码率R比原码要小，但纠错能力不一定比原码强。因此，总的看来，缩短码的性能比原码的性能要差。

【例6.37】（续例6.36）

例6.36中的二元（7，4，3）Hamming码，选出最高位码元为0的码字组成二元（6，3）缩短码000000，011110，101101，110011，000111，011001，101010，110100。

与缩短码构造过程相反的码是延长码。

定义6.58 （n，k，d）线性分组码C先进行增广，再将得到的增广码进行扩展，则最后的（n+1，k+1）扩展码称为原码C的延长码。

可见，延长码是在原（n，k，d）码C的基础上，先进行增广然后再加一个全校验元构成的。因此，延长码的码率为（k+1）/（n+1），比原码的码率k/n要大一些，其码的最小距离也可能与原码相同。

【例6.38】

二元（7，3，4）增余删信Hamming码先进行增广，变成二元（7，4，3）Hamming码，然后再增加一个全校验元，变成二元（8，4，4）扩展Hamming码。该码比原来的二元（7，3，4）码的码率要高，而最小Hamming距离相同。以二元（7，3，4）Hamming码为例，把上述各类码之间的关系，示于图6.6中。

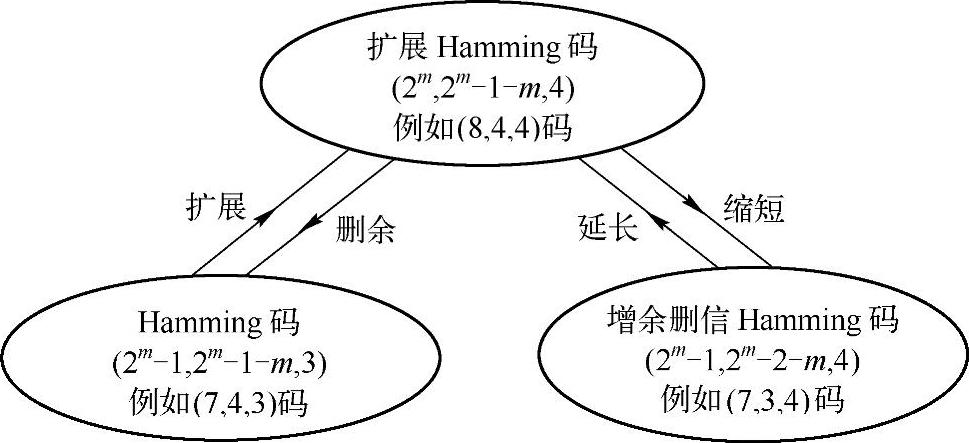
图6.6 二元Hamming码的各类修正码之间的关系图