伴随式和标准阵列译码技术优化探讨

1.伴随式及伴随式译码

在GF（q）上，设发送码字为c=（c₀，c₁，…，c_n-1），通过有扰信道传输，信道产生的错误图样为e=（e₀，e₁，…，e_n-1）；收信端收到的n维矢量为r=c+e=（r₀，r₁，…，r_n-1）；r_i，c_i，ei∈GF（q）；r_i=c_i+e_i。译码器的任务就是从接收码字r中估计发送码字c的估值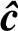，或者由r中解出错误图样的估值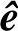，从而得到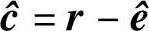，并使译码错误概率最小，或使估值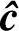尽可能是发送码字c。

线性分组码的每个码字c都必须满足cH^T=0或Hc^T=0。因此，收到接收码字r后用该两式之中的任一式进行检验：

rH^T=（c+e）H^T=cH^T+eH^T=eH^T （6.44）

若e=0，则rH^T=0；若e≠0，则rH^T≠0。这说明rH^T仅与错误图样有关，而与发送码字无关。为此，给出下面定义。

定义6.51 设线性分组码的发送码字为c，接收码字为r，信道的错误图样为e，则

s=rH^T=eH^T（6.45）

称为接收码字r的伴随式（或校正子）。

如果译码器仅用于检错译码，则只需要计算接收码字r的伴随式s，若s≠0，则判定接收码字r有错误；否则，判定接收码字r没有错误。

伴随式s完全由e决定，它充分地反映了信道的干扰情况。纠错译码器的主要任务就是如何从s中得到最像错误图样e的估值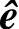，从而译出。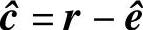

设在第i₁，i₂，…，i_t位有错的错误图样e为

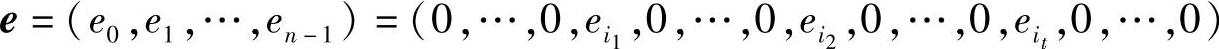
用式（6.42）的一般形式的线性分组码的校验矩阵对这个错误图样e进行校验，有

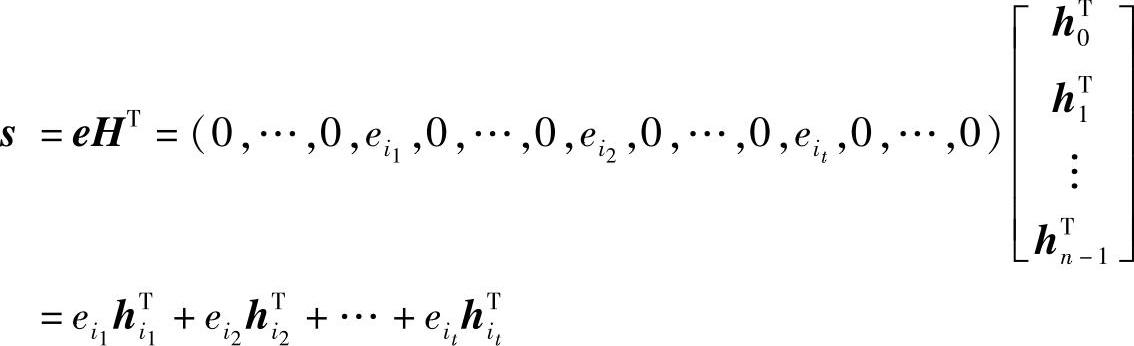
式中，h_i为H矩阵的第i列，是n-k维列矢量。

上式表明，s是H矩阵中相应于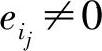（j=1，2，…，t）的列h_ij的线性组合，由于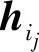是n-k维列矢量，故s是n-k维的行矢量（s₀，s₁，…，s_n-k-1）。若接收码字r没有错误，所有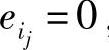，则s是一个零矢量。

【例6.32】（续例6.30）

设二元（7，3，4）线性分组码的发送码字c=（1001101），e=（1000100），则接收码字r=（0001001）。由式（6.45）知，s=rH^T=（1111），它是H矩阵第1与第5列之和的转置。若错误图样e=（0100010），s=rH^T=（1111），它是H矩阵第2与第6列之和的转置。若错误图样e=（0010000），则s=rH^T=（0010）是H矩阵第3列的转置。

从例6.32的计算看出，若错误图样只有一个分量非零，其他均为0，则s≠0，且是H矩阵相应的列。因此，当n长码字中发生在不同位置上的单个错误时，就得到不同的非0伴随式（假设H的每列均不同），由这些不同的伴随式就可以求得不同的错误图样e。因此，例6.32的（7，3，4）码能纠正单个错误。若发生两个错误，则s≠0，但不能纠正。如例6.32中第1、5位发生错误与第2、6位发生错误，所得到的伴随式均相同。因此，由于伴随式不为0，译码器只能判决传输有错（e≠0），但不能唯一地判定是由哪几位错误引起的。可见该码能纠正一个错误，同时发现两个错误。这是很显然的，因为该码的最小距离为4。

从上面分析看出，一个线性分组码要纠正≤t个错误，则要求≤t个错误的所有可能组合的错误图样，都应该有不同的伴随式与之对应。

利用伴随式进行（n，k，d）线性分组码的译码步骤归结为以下三步：(www.xing528.com)

1）由接收码字r计算伴随式s=rH^T。

2）若s=0，则认为接收码字无误；若s≠0，则由s找出错误图样的估值。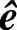

3）计算发送码字的估值。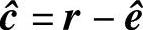

不难分析，对于纠正单个错误的线性分组码，由于伴随式s、错误图样e和校验矩阵H的列有简单的对应关系，因此，利用伴随式译码法是很简单的。除此以外，对其他线性分组码而言，如何由s求得错误图样的估值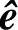就比较复杂。而译码器的复杂性及其译码错误概率也往往由这一步决定。下面讨论分组码的一般译码方法，即标准阵译码法，它是由Slepian于1956年提出的，是一种在BSC信道中译码错误概率最小的译码方法。

2.标准阵

q元（n，k，d）线性分组码的q^k个码字组成n维线性空间的一个k维子空间，该子空间是子群。利用前面的群的基本知识，若以此子群为基础，对n维空间全部qⁿ个元素按陪集划分，则得到表6.5所示的译码表。其中，q^k个码字放在表中的第一行，子群的恒等元c₁=（00…0）（0矢量）放在最左边。在禁用码字中选一个n维矢量e₂放在恒等元素c₁的下面，并求出c₂+e₂，c₃+e₂，…，c_qk+e₂，分别放在c₂，c₃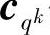，…，码字的下边构成第二行，这是码空间（子群）的一个陪集。再选一个未写入表中前一行的n维矢量e₃，用以上方法构成另一陪集作为表中的第三行。依次类推，共构成q^n-k个陪集，称c₁=e₁，e₂，e₃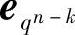，…，为陪集首。根据群论的陪集理论，这种划分把全部qⁿ个矢量划分完毕，且不出现重复元素。按这种方法构成的表称为标准阵译码表，简称标准阵。

表6.5 标准阵译码表

如果接收码字（n维矢量）r落在某一列中，则译码器就将r译成相应于该列最上面的码字。因此，若发送码字c_j，接收码字r=c_j+e_j（j=1，2，…，q^k，e₁是全0矢量），则能正确译码；如果接收码字r=c_k+e_j，则产生了错误译码。

从上述的标准阵译码原理可以看出，标准阵译码法可以纠正的错误图样就是全部的陪集首。由于陪集的划分主要取决于子群，而子群就是q^k个码字，对译码来说，这是已知的。因此，为使标准阵译码的译码错误概率最小，就应该合理选择陪集首。

理论分析表明，在对称DMC信道条件下（此时，产生随机性错误），n长接收码字中出现错误个数少的图样，其概率比出现错误个数多的图样大，即错误图样重量越小的图样产生的可能性越大。因此，译码器必须首先保证能正确纠正这种可能性出现最大的错误图样，也就是重量最轻的错误图样。这相当于在构造译码表时要求挑选重量最轻的n维矢量为陪集首，放在标准阵中的第一列，而以全为0码字作为子群的陪集首。这样得到的标准阵，能得到最小的译码错误概率。由于这样安排的译码表使得c_i+e_j与c_i的距离保证最小，因此，也称为最小距离译码。在对称DMC信道条件下，它们等效于最大似然译码。

【例6.33】（续例6.24）

例6.24给出了二元（6，3）线性分组码的8个码字，该码的标准阵见表6.6。

表6.6 （6，3）线性分组码标准阵

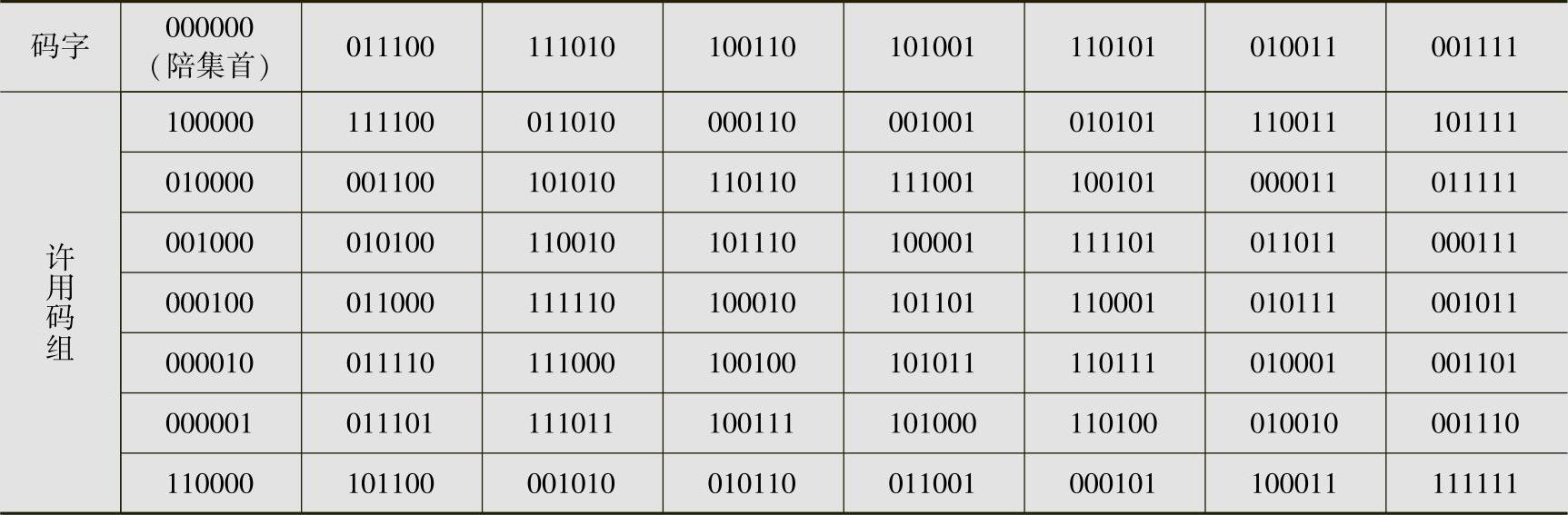
由表6.6看到，标准阵译码法需要把q^k个n维矢量存储在译码器中。所以，这种译码方法译码器的复杂性随n指数增长，很不实用。

根据错误图样与伴随式之间的一一对应关系，可以简化标准阵，得到一个简化译码表。如例6.33中的（6，3）线性分组码标准阵，可以简化为表6.7所示的译码表。译码器收到r后，计算伴随式s=rH^T，由s查表得到错误图样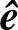，从而译出码字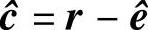。因此，这种译码器不必存储所有qⁿ个n维矢量，而只存储错误图样e与q^n-k个n-k维矢量s。

表6.7 （6，3）线性分组码简化译码表

通常，（n，k，d）分组码n、k都比较大，即使用这种简化译码表，译码器的复杂性还是很高。译码器要存储如此多的错误图样e和n-k维矢量s也是不太可能的。因此，在线性分组码理论中，实现简化译码器是最核心的研究课题之一，这将在以后有关章节中讨论。