生成矩阵、一致校验矩阵和对偶码简介

1.生成矩阵

q元（n，k）线性分组码的编码问题就是在n维线性空间V^q_n中，找出满足一定要求的、有q^k个矢量组成的k维线性子空间V^q_n，k。或者说，在满足给定条件（码的最小Hamming距离d或码率R）下，建立一组如式（6.27）所示的编码方程，并要求这一组方程是线性方程组。通过该方程，由k个码元组成信息组m=（m₀，m₁，…，m_k-1），求出码字c=（c₀，c₁，…，c_n-1），使得到的码恰好具有所要求的最小距离d。这样的一组线性编码方程写为

c_i=m₀g₀，i+m₁g₁，i+…+m_k-1g_k-1，i，i=0，1，…，n^-1 （6.34）

将式（6.34）中的n个线性方程写成矩阵形式，有

式中，。

式（6.35）表明，当已知待编码的信息组m后，计算c=mG就完成了线性分组码的编码。因此，称GF（q）上k×n阶矩阵G为线性分组码的生成矩阵。显然，生成矩阵的行空间就是n维线性空间V^q_n的k维线性子空间V^q_n，k。当然，线性分组码的生成矩阵也可以由生成子空间的一组矢量基底导出。

【例6.28】

二元（7，3，4）线性分组码的生成矩阵G₁为

用3长的全部信息组m=000～111，计算c=mG₁得该码的全部8个码字为

000↔0000000 001↔0010111

100↔0111100 101↔0101011

010↔1001101 011↔1011010

110↔1110001 111↔1100110

【例6.29】

二元（7，3，4）线性分组码的生成矩阵G₂为

用3长的全部信息组m=000～111，计算c=mG₂得该码的全部8个码字为

000↔0000000 001↔1110001

100↔0111100 101↔1001101

010↔1011010 011↔0101011

110↔1100110 111↔0010111

比较例6.28和例6.29两种不同的（7，3，4）码的生成矩阵G₁和G₂，以及由它们生成的两种线性分组码，发现这两种码的集合是相同的，差别仅是信息组与码字的对应关系不同。因此，这两种码的纠错能力是相同的。另外，例6.29的（7，3，4）线性分组码的信息组以不变的形式出现在码字的后3位上，这种形式的码在解码时比较方便。为此，产生了系统码的概念。

定义6.48 若（n，k）线性分组码的信息组以不变的形式在码字的任意k位出现，称这种码为系统码，否则称为非系统码。

在后续的讨论中约定，系统码的信息组出现在（n，k）线性分组码码字的后k位上，其前面的n-k位称为校验元。显然，系统码的信息组码元与校验元很容易区分开，所以这种码也称为可分码。在系统码条件下，q元（n，k）系统码的生成矩阵的一般形式是

G=[P I_k] （6.38）

式中，P是GF（q）上k×（n-k）阶矩阵；I_k是k阶单位矩阵。

2.校验矩阵

从系统码生成矩阵G=[P I_k]，可以构造出另一个重要的（n-k）×n阶矩阵

H=[I_n-k-P^T] （6.39）

式中，P^T表示P的转置矩阵。对于二元码，+1=-1，所以，式（6.39）中的负号可以去掉。

称矩阵H是（n，k）线性分组码的一致校验矩阵，简称校验矩阵。这是因为对任意码字c=mG，计算cH^T=0，即

也就是说，（n，k）线性分组码的每个码字与H矩阵的每一行正交，这构成了码字中n-k个校验元所需要满足的校验方程。实际上

式中，0_k×（n-k）是k×（n-k）阶零矩阵。式（6.41）表明，由G矩阵的行矢量张成的k维子空间与由H矩阵的行矢量张成的n-k维子空间是正交的。(https://www.xing528.com)

由于H矩阵的行矢量张成的n-k维子空间的基底可以有多个，则其任一组基底矢量作为行矢量，可以组成满足式（6.41）的H矩阵。因此，一致校验矩阵的一般形式为

式中，h_i是H矩阵的第i列，是n-k维列矢量。

【例6.30】（续例6.28和例6.29）

由例6.29的二元（7，3，4）线性分组码的生成矩阵G₂，可以得到该码校验矩阵为

可以检验G₁H^T=0，G₂H^T=0，其中G₁和G₂是例6.28和例6.29码的生成矩阵。

系统码的编码相对而言较为简单，且由生成矩阵G可以方便地得到校验矩阵H（反之亦然），容易检查编出的码字是否正确。同时，对分组码而言，系统码与非系统码的纠错能力完全等价。因此，今后若无特别声明，仅讨论系统码形式。

校验矩阵H与码的最小Hamming距离d有密切联系，为此，给出下面的重要定理。

定理6.27 GF（q）上（n，k）线性分组码的最小Hamming距离等于d的充要条件是，H矩阵中任意d-1列线性无关。

证明 先证明必要性。即码有最小距离为d，证明H中的任意d-1列线性无关。用反证法。若矩阵H中某d-1列线性相关，则由线性相关定义知

h_ij是矩阵H的列矢量。设一矢量在i₁，i₂，…，i_d-1位处取值分别为c_i1，c_i2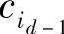，…，，其他位取值为0，这样得到矢量c=（0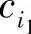，…，0，，0，…，0，，0，…，0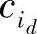，，0，…，0），由此

故c是一个码字，而c的非0分量个数只有小于等于d-1个，这与码有最小距离为d的假设相矛盾，故矩阵H中的任意d-1列必线性无关。

再证明充分性。即证明，若H矩阵中任意d-1列线性无关，则（n，k）线性分组码的最小距离为d。若H矩阵中任意d-1列线性无关，则H中至少需要d列才能线性相关。将能使H中某些d列线性相关的列的系数，作为码字中对应的非0分量，而码字的其余分量均为0，则该码字至少有d个非0分量，故码有最小距离为d。

【证毕】

由定理6.27，并结合码的纠错能力，可以直接得到下面的定理。

定理6.28 一个（n，k，d）线性分组码，若要纠正≤t个错误，则其充要条件是H矩阵中任何2t列线性无关。

定理6.28非常重要，它是构造任何类型线性分组码的基础。该定理表明，交换H矩阵的列，不会影响线性分组码的最小距离。因此，所有列相同，但排列位置不同的H所对应的线性分组码，其纠错能力和其他码参数完全等价。

定理6.29（Singleton限）线性分组码的最大可能的最小距离d≤n-k+1。

证明 因为线性分组码的H矩阵是（n-k）×n阶矩阵，因此，H矩阵的最大线性无关列的数目是n-k，故线性分组码的最大可能的最小距离为n-k+1。

【证毕】

定义6.49 若分组码的最小距离d=n-k+1，称此码为极大最小距离可分码。

构造极大最小距离可分码是编码理论中一个重要课题，后面讨论的RS码就是一种极大最小距离可分码。

3.对偶码

（n，k）线性分组码是n维线性空间V_n中的一个k维子空间V_n，k，由一组基底即生成矩阵G的行矢量张成。由前可知，它的零空间必是一个n-k维的线性子空间V_n，n-k，并由n-k个独立矢量张成。由式（6.39）和式（6.42）知，这n-k个矢量就是H矩阵的行矢量。因此，若把H矩阵看成是（n，n-k）线性分组码的生成矩阵，而把（n，k）线性分组码的生成矩阵G看成是它的校验矩阵，则称由G生成的（n，k）线性分组码C与由H生成的（n，n-k）线性分组码C^⊥互为对偶码。相应地，称V_n，k与V_n，n-k空间互为对偶空间。

定义6.50 设C是（n，k）线性分组码，则它的对偶码C^⊥是

C^⊥={a∈V_n，n-k|所有b∈V_n，k，使a·b=0}（6.43）

式中，a·b为a与b的内积。

【例6.31】（续例6.29）

例6.29的（7，3）线性分组码，它的对偶码必是（7，4）线性分组码，其生成矩阵G（7，4）就是（7，3）线性分组码的校验矩阵H（7，3），即

由此生成矩阵，已知信息组，计算c=mG就可以求得（7，4）线性分组码的16个码字。

若一个码的对偶码是其本身，即C=C^⊥，则称C码为自对偶码。显然，自对偶码必定是（2m，m）形式的分组码。如（2，1）重复码就是一个自对偶码。