分组码的基本概念探究

1.分组码的定义

从信源输出的以k个码元为一组的信息组m，通过纠、检错编码器后，变换成n（通常n＞k）长的码字（也称为码组）c，即编码器给k个码元的信息组按一定规则映射成n个码元，组成n长的码字。编码规则使码字中的n个码元之间建立一种关系，如满足一组方程（线性的或非线性的）。而收信端的译码器从收到的n长序列r中按编码规则来检验这些关系（或方程），从而确定r中是否有错误，并自动予以纠正。

码字中的n个码元通常取自q个符号，即q元编码或q进制编码。但由于广泛使用的数字处理技术为二元码制，因此，二元编码和2^m元编码是最常用的编码进制。今后，如无特别说明，所讨论的码均指二元码。

n长q元序列（今后称为n维矢量）共有qⁿ个，分组码的编码问题就是定出一套规则，从qⁿ个n维矢量中选出M个作为码字。下面给出分组码的一般性定义。

定义6.42 在q元qⁿ个n维矢量中，取出M个n维矢量组成的集合称为q元[n，M]分组码，称被选出的M个n维矢量为许用码字，其余的qⁿ-M个n维矢量为禁用码字。该码的编码速率（或称码率）为。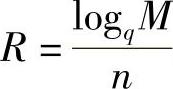

通常取M=q^k。但有些分组码，如后面将介绍的恒比码，M≠q^k。为方便起见，[n，M=q^k]分组码简记为（n，k）分组码。显然q元（n，k）分组码有q^k个许用码字，码率为R=k/n。

由定义6.42知，不同的选取规则，就组成了不同的[n，M]分组码。对于给定的码长n和许用码字数M，所有可能的不同的编码方法共有（qⁿ）M=q^nM种，其中，只有极小部分的编码是性能优良的码。

用数学语言对分组码的定义描述如下：

设M个q元k长信息组m=（m₀，m₁，…，m_k-1），一种q元[n，M]分组码的编码方法就是确定一组n个编码函数，将k长信息组m映射成n长码字c=（c₀，c₁，…，c_n-1），这组函数写为

c_i=f_i（m₀，m₁，…，m_k-1），i=0，1，…，n^-1 （6.27）

在分组码中存在一大类线性分组码。由于线性分组码具有优良的数学结构、很强的纠错和检错能力，与非线性分组码相比，其编码和译码算法又比较简单。因此，线性分组码获得了广泛的关注，并在工程中得到了大量的应用。下面重点讨论线性分组码。

如果将（n，k）线性分组码看成是n维数组或n维线性空间中的一组矢量，就可以用线性空间理论深入地研究线性分组码。（n，k）线性分组码是把待编码的信息序列划分成k个码元组成的信息组，通过编码器变换成为n个码元的一组，作为（n，k）线性分组码的一个码字。若每位码元的取值有q种（通常q为素数，或素数幂），则共有q^k个码字。n维数组共有qⁿ个（二元时有2ⁿ个）。显然，qⁿ个n维组成GF（q）上的n维线性空间。如果q^k个码字集合构成一个k维线性子空间，则称它是一个（n，k）线性分组码。

定义6.43 （n，k）线性分组码是GF（q）上的n维线性空间V^q_n中的一个k维子空间V^q_n，k。该码的编码速率（码率）为R=k/n。

线性子空间在加法运算下构成Abel群，所以线性分组码又称为群码。线性分组码的码元的值域是GF（q），其中q=p^m，p为素数，m为正整数。

由于线性分组码的全体码字构成一个群，因此，具有以下性质：

性质6.8 线性分组码中任意两个码字的和是该码集合中的一个许用码字。

在通信系统或计算机系统中，多以二元表示信息，因此，常使用的线性分组码是二元码或2^m元码。为简单起见，如无特别说明，所讨论的分组码均指线性分组码。

一般用c=（c₀，c₁，…，c_n-1）表示q元（n，k）线性分组码的任一码字，码字c的每一分量c_i∈GF（q）（i=1，2，…，n-1）。

【例6.24】

二元（6，3）线性分组码的编码如下，这8个码字构成Abel加群。

信息组 码字 信息组 码字

000↔000000 001↔101001

100↔011100 101↔110101

010↔111010 011↔010011

110↔100110 111↔001111

2.Hamming距离和Hamming重量

下面系统地介绍分组码的汉明距离（Hamming距离）和汉明重量（Hamming重量）的概念。

定义6.44 两个n维矢量a和b的对应分量不相同的个数，称为它们之间的Hamming距离，简称距离，记为d（a，b）。

设a=（a₀，a₁，…，a_n-1）和b=（b₀，b₁，…，b_n-1），显然，有下式成立：

d（a，b）=d（a₀，b₀）+d（a₁，b₁）+…+d（a_n-1，b_n-1） （6.28）

【例6.25】

二元7维矢量a₁=（0100110），b₁=（1010100），则其Hamming距离d（a₁，b₁）=4；

四元6维矢量a₂=（301012），b₂=（203002），则其Hamming距离d（a₂，b₂）=3。

Hamming距离是一种距离的测度，亦应满足下列性质：

性质6.9 自反性 任意n维矢量a，则有d（a，a）=0。

性质6.10 非负性 任意n维矢量a和b，则有d（a，b）≥0。

性质6.11 对称性 任意n维矢量a和b，则有d（a，b）=d（b，a）。

性质6.12 三角不等式 任意n维矢量a、b和c，则有d（a，b）+d（b，c）≥d（a，c）。

上述性质的证明留作习题。

一个q元（n，k）分组码C的q^k个码字集合中，两两码字的距离必有一个最小值。故有

定义6.45 分组码C的最小Hamming距离d为

最小Hamming距离是衡量一个分组码的纠错或检错能力的一个极为重要的参数。因此，有时为表述问题方便，常将最小Hamming距离为d的分组码（n，k）记为（n，k，d），将分组码[n，k]记为[n，k，d]。根据讨论的问题需要，这两种记法在后面是混用的。

【例6.26】（续例6.24）(www.xing528.com)

在例6.24的码中，共有8个码字，分别求出两两码字的距离，取其最小者。易知最小Hamming距离d=3。因此该码是二元（6，3，3）线性分组码。

按定义确定一个码的最小距离，就必须分别求出两两码字的距离，并取其最小值。如果码字的个数很多，其运算量就很大。为解决这个问题，引入Hamming重量的概念。

定义6.46 n维矢量a=（a₀，a₁，…，a_n-1）中非零元素的个数称为a的Hamming重量，简称重量，记为w（a）。

定义6.47 分组码C中不等于0的码字重量的最小值w称为码C的最小Hamming重量（简称最小重量），其定义式为

【例6.27】（续例6.24）

在例6.24中，除全0码字外，该二元（6，3）线性分组码的各码字重量为3、4、3、3、4、3、4，故该码的最小重量w=3。

定理6.23 线性分组码的最小Hamming距离等于它的最小Hamming重量。

证明 由性质6.8的封闭性知，线性分组码中任意两个码字之间的Hamming距离一定是某一个许用码字的Hamming重量，因此，定理6.23必成立。

【证毕】

定理6.24 线性分组码的码字Hamming重量或全部为偶数，或奇、偶重量码字数相同。

证明 设线性分组码有偶重量码字n₁个，奇重量码字n₂个。若n₂=0，则定理成立。

若n₂≠0，将某一奇重量码字与所有n₁个偶重量码字相加，由性质6.8的封闭性知，将得到n₁个奇重量码字。因此，必有n₁=n₂。同时，可以推出n₁≠0，即没有仅含有奇重量码字的线性分组码存在。

【证毕】

3.码的纠错能力

两个矢量之间的Hamming距离表示它们之间差别的大小。距离越大，则从一个矢量变成另一个矢量的可能性越小。在最大似然译码中，所谓一个码字“最像”另一个码字，即指它们的距离最小。码的最小Hamming距离是衡量码抗干扰能力的重要参数。码的最小距离越大，其抗干扰能力越强。码的抗干扰能力一般可以分为下列三种情况讨论：

1）检测l个错误。系指码字传送时出现错误的个数≤l，该码的译码器都能发现。

2）纠正t个错误。系指码字传送时出现错误的个数≤t，该码的译码器能纠正，即可以从接收码字中恢复成原发送码字。

3）纠正t个同时检测l个错误（l＞t）。系指码字传送时出现错误的个数≤t时，该码的译码器能纠正；出现错误的个数＞t但≤l时，译码器虽不能纠正但可以发现。

一个码的最小距离d和码的抗干扰能力有如下关系：

定理6.25 对于（n，k，d）分组码

1）检测l个差错的充要条件是d≥l+1。

2）纠正t个差错的充要条件是d≥2t+1。

3）纠正t个差错，并检测l个差错的充要条件是d≥t+l+1，其中l＞t。

证明 设a、b是（n，k，d）分组码中的两个码字。

1）一方面，若d≥l+1，a传送时出错个数≤l，且接收码字为r，则d（a，r）≤l。由于d≥l+1，说明r不是许用码字。因此，根据r判定传送出现了≤l个差错，故该码是可以检测l个错误的码。

另一方面，因a、b均是码字，故d（a，b）≥d≥l+1。若发送a，接收码字是r且传送时发生l+1个错误，则d（a，r）=l+1。此时，若r=b，则r是许用码字，而无法检测出是否出现错误，即该码不能检测出l+1个错误。

综上两方面，该（n，k，d）分组码检测l个错误的充要条件是d≥l+1。

2）一方面，若d≥2t+1，则d（a，b）≥2t+1。若发送a，接收码字是r且传送时发生错误个数≤t，则

d（a，r）≤t （6.31）

当b是（n，k，d）分组码中任一码字时，由性质6.12得

d（a，r）+d（r，b）≥d（a，b）≥2t+1 （6.32）

由式（6.31）和式（6.32）得d（r，b）≥t+1。这就是说，r与任意一个不等于a的码字的距离都满足≥t+1，与a的距离≤t。根据最大似然译码准则，r与a的距离最小，故将r译成a。因此，该码是可以纠正t个错误的码。

另一方面，若d（a，b）≥2t+1，那么总可以找到一个字r，使d（a，r）≥t+1，d（b，r）=t。当发送a且发生≥t+1个错误变成r时，有d（r，b）＜d（a，r）。根据最大似然译码准则，译码器将r译成b而不是a，也就是说发生错误译码。

综上两方面，该（n，k，d）分组码纠正t个差错的充要条件是d（a，b）≥2t+1。

3）由1）和2）很容易证明，故从略。

【证毕】

定理6.26 二元（n，k）线性分组码中，任何两个码字a、b之间有如下关系：

w（a+b）=w（a）+w（b）-2w（a·b）（6.33）

式中，a·b是两个码字的内积。

证明 设a=（a₀，a₁，…，a_n-1）和b=（b₀，b₁，…，b_n-1）。

考查w（a_i+b_i），当a_i、b_i取值为00，01，10，11时，有w（a_i+b_i）=w（a_i）+w（b_i）-2w（a_i·b_i）成立。又因为w（a）=w（a₀）+w（a₁）+…+w（a_n-1），所以，必有式（6.33）成立。

【证毕】