由前面讨论知,以素数p为模的整数同余类环构成p阶有限域GF(p)。以GF(p)上m次首一既约多项式g(x)为模的多项式同余类环构成pm阶有限域,通常用GF(pm)表示。由于有限域理论在编码理论中起着特别重要的作用,故下面将较详细地讨论它的乘法结构、加法结构等代数结构。
1.有限域的乘法结构
域的全体非0元素集合构成交换乘群;全体元素集合构成交换加群。
有限域的元素个数是有限的。因此,全体非0元素集合构成有限乘群,乘群中每个元素的级为有限。并可以证明,该群必由群中的一个元素生成,且是循环群。
定义6.25 域中非0元素构成乘群,该乘群元素的级定义为域中该元素的级。
定义6.26 若α为GF(q)中的n级元素,则称α为n次单位原根。若在GF(q)中,某元素α的级为q-1,则称α为本原域元素,简称本原元。
由于GF(q)中全体q-1个非0元素集合组成乘群,因此,本原元α能生成这个乘群,与循环群中的定义类似,显然有αq-1=1。
定理6.14 GF(q)中的每个非0元素是多项式xq-1-1=0的根;反之,多项式xq-1-1=0的根必在GF(q)中。
推论6.3 由GF(q)中n级元素α生成的循环群G(α),一定是xn-1=0的根。
GF(q)中的全体q-1个非0元素集合组成循环群。换言之,q-1个非0元素一定可以由一个级为q-1的本原元生成。
由上述可知,若α是GF(q)中的本原元,则可以把xq-1-1在域中完全分解成一次因式

称GF(q)为xq-1-1的最小完全分离解(域)。
2.有限域的加法结构
在域中必有乘法单位元1,若作1+1+1+…运算,对无限域来说,则有可能n·1≠0,但在有限域中,1+1+…+1=0,否则该域必成为无限域。例如,在GF(2)中,1+1=0。
定义6.27 满足n.1=0的最小正整数n,称为域的特征。如果对于每一个n,恒有n.1≠0,则称该域的特征为∞。
【例6.16】
GF(2)的特征为2;若p为素数时,GF(p)的特征为p。
定理6.15 在特征为p的域中,若a是域中的任意元素,则均有pa=0。
定理6.16 每一个域的特征或为素数,或为∞。
有限域的特征必为有限;但当域的特征为有限时,该域可以是有限域也可以是无限域。
【例6.17】
p为素数,GF(p)上全体多项式集合关于多项式加法和乘法运算构成一个域,它的单位元为1,且p·1=0,所以域的特征为p。但集合中多项式的次数可以是无限的,故集合中的元素个数是无限的。因此,这是一个有限特征的无限域。
定义6.28 以p为特征的域是GF(pm)(m=1,2,…),称GF(p)是GF(pm)的基域,GF(pm)为GF(p)的扩域,称GF(p)为素子域(或称素域)。
可以证明,GF(q)的阶q一定是素数或素数的幂,即q=pm(m=1,2,…;p是素数),且域的特征为p。近一步由定理6.13知,GF(pm)是通过构造GF(pn)上模k次多项式g(x)(k,n=1,2,…;m=kn)的多项式同余类集合得到的。
总结上述分析可知,GF(pm)可以由:①GF(p)上模m次多项式,或②GF(pn)上模k次多项式,或③GF(pk)上模n次多项式构成,其中m=kn;GF(pn)由GF(p)上模n次多项式构成;GF(pk)由GF(p)上模k次多项式构成。因此,GF(p)是GF(pk)、GF(pn)和GF(pm)的素子域;GF(pk)和GF(pn)是GF(pm)的子域,同时也是GF(p)的扩域;GF(pm)是GF(p)、GF(pk)和GF(pn)的扩域。
利用这种子域与扩域的相互关系,可以构造出许多复杂、巧妙的代数系统,这些系统在信道编码理论和密码理论中得到了广泛应用。
定理6.17 在特征为p的域中,有下列性质:
1)若a是域中的任意元素,则均有(x-a)p=xp-ap和 。
。
2)若a和b是域中的任意元素,则均有(a±b)p=ap±bp。
3)任意域元素的级均不是p的倍数。
4)设f(x)是GF(p)上的n次多项式,若p特征域中的元素β是f(x)的根,则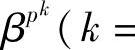
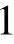 ,2,…)也是f(x)的根。
,2,…)也是f(x)的根。
在GF(pm)中,本原域元素的级是pm-1,而其他域元素的级必是pm-1的因子。在GF(2m)中,本原域元素和其他一切域元素的级均是奇数。
3.最小多项式和本原多项式
由于多项式f(x)是n次多项式,其根不多于n个。因此,定理6.17中4)给出的f(x)的根序列β,βp, ,…中必有重复,且不多于n个。设这样的不重复的根数为k个,则这k个根写成β,βp,
,…中必有重复,且不多于n个。设这样的不重复的根数为k个,则这k个根写成β,βp,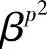 ,…,
,…, 。为此,引出共轭根系的定义。(https://www.xing528.com)
。为此,引出共轭根系的定义。(https://www.xing528.com)
定义6.29 若多项式f(x)以β为根,则称β,βp, ,…,
,…,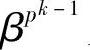 为共轭根系。
为共轭根系。
如果β是p特征域上的n级元素,βn=1,则β是系数取自GF(p)上的多项式xn-1的根。系数取自GF(p)上,且以β为根的多项式可以有多个,其中必有一个次数最低的多项式。
定义6.30 系数取自GF(p)上,且以β为根的所有首一多项式中,必有一个次数最低的多项式,称之为最小多项式,记为m(x)。
定理6.18 在p特征有限域中,每一个元素β,皆存在唯一的最小多项式m(x),具有以下性质:
1)m(x)在GF(p)上是既约的。
2)若f(x)是GF(p)上的多项式,且f(β)=0,则m(x)f(x),显然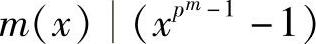 。
。
定理6.19 设β是p特征有限域中的元素,若β,βp,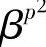 ,…,
,…,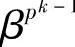 为一组共轭根系,则β的最小多项式m(x)是k次的,且为
为一组共轭根系,则β的最小多项式m(x)是k次的,且为

定义6.31 系数取自GF(p)上,以GF(pm)中本原元为根的最小多项式,称为本原多项式。
由定义6.31知,本原多项式一定以n=pm-1级元素为根。设α为本原元,则以α为根的本原多项式的共轭根系是α,α ,
,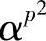 ,…,
,…, ,共有m个根。因此,以GF(pm)上的本原元为根的GF(p)上的本原多项式,必是m次多项式。
,共有m个根。因此,以GF(pm)上的本原元为根的GF(p)上的本原多项式,必是m次多项式。
定义6.32 设f(x)是GF(p)上次数>1,而零次项不为0的多项式,称满足f(x)xn-1的最小正整数n为f(x)的周期,记为p(f)=n。
定义6.33 若f(x)是GF(q)上的n次多项式,称 为f(x)的互反多项式。
为f(x)的互反多项式。
互反多项式有如下性质:
性质6.5 若α是f(x)的根,则α-1必是f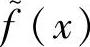 的根。
的根。
性质6.6 若f(x)是既约多项式,则 也是既约多项式,反之亦然。
也是既约多项式,反之亦然。
性质6.7 若f(x)是本原多项式,则f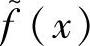 也是本原多项式,反之亦然。
也是本原多项式,反之亦然。
可以证明,m次本原多项式的周期为pm-1,且m次多项式是本原多项式的充要条件是其周期为pm-1。
【例6.18】
f1(x)=x3+x+1,f2(x)=x4+x3+x2+x+1,f3(x)=x4+x+1,f4(x)=x4+x3+x2+1均是GF(2)上的多项式。因为x7+1=(x+1)(x3+x+1)(x3+x2+1),(x+1)(x3+x+1)=f4(x),故知p(f1)=p(f4)=7;又因为x5+1=(x+1)f2(x),故有p(f2)=5;实际上,f3(x)x15+1,故有p(f3)=15。可以验证,f1(x)、f2(x)、f3(x)是既约多项式,f4(x)不是既约多项式。
既约多项式f1(x)、f3(x)是本原多项式,因为p(f1)=23-1=7,p(f3)=24-1=15。而f2(x)是非本原多项式,因为p(f2)=5≠24-1=15。
由定义知,本原多项式必是既约多项式,但反之不一定。对于正整数m,至少有一个m次本原多项式。但m次本原多项式可能有多个。可以证明,m次本原多项式有φ(pm-1)/m个,其中φ(n)是欧拉函数,是指当n为自然数,不超过n且与n互素的正整数的个数。
【例6.19】
x3+x+1和x3+x2+1是GF(2)上两个3次本原多项式,且这两个多项式是互反多项式。
本原多项式在编码理论中十分重要,而确定本原多项式是很困难的。为方便读者,表6.3给出了GF(2)上次数40以内的本原多项式,每个长度仅列出一个。
表6.3GF(2)上m≤40次的本原多项式
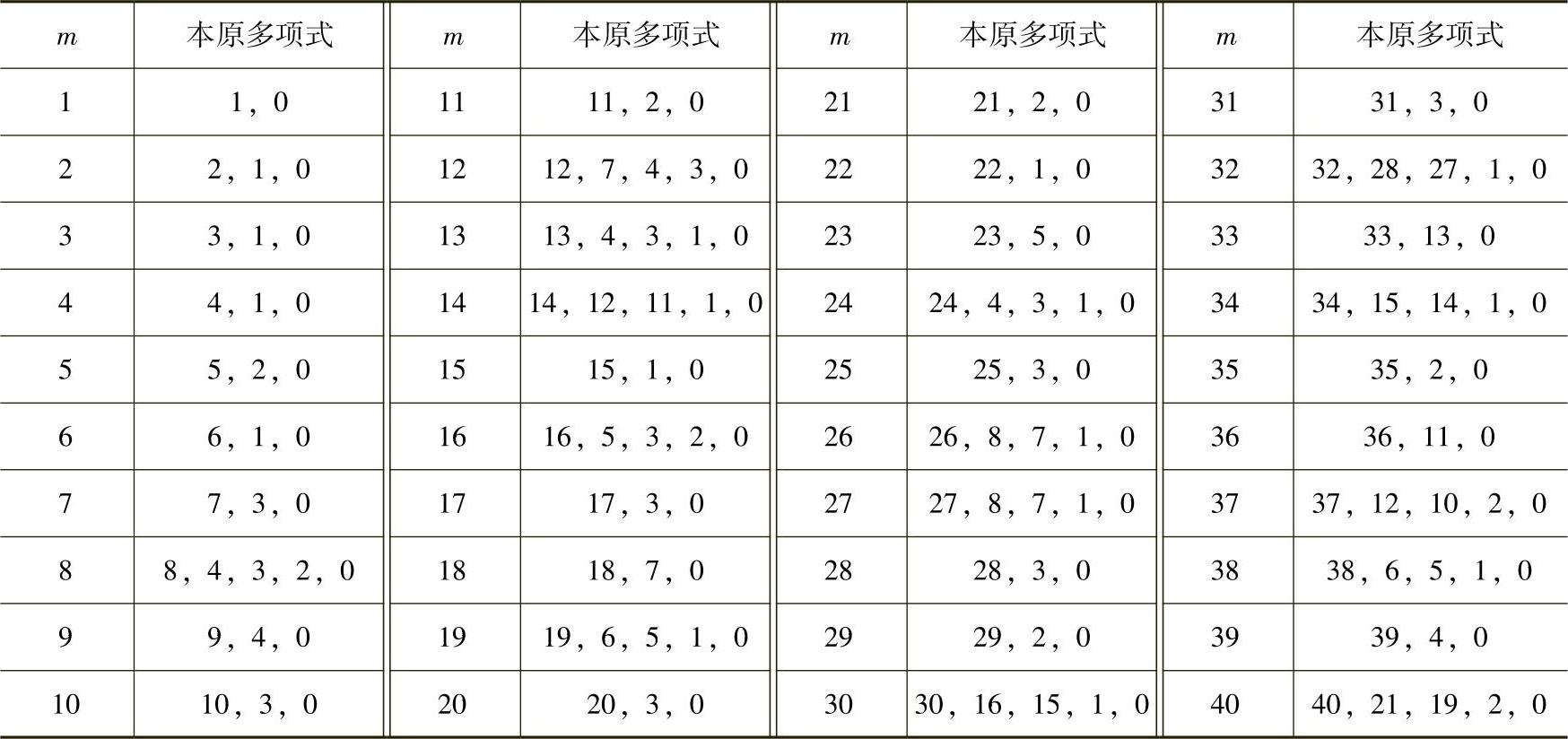
注:表中所列数字表示多项式非零系数所对应的幂次,如10次本原多项式为m(x)=x10+x3+1。
4.用本原多项式构造有限域
前面已经讨论了有限域的性质和多种有限域GF(pm)的表示方法。由于有限域理论是讨论循环码的重要的数学基础,下面以有限域GF(24)为例,详细给出用本原多项式构造有限域的方法与加法和乘法的计算方法。
查表6.3知4次多项式x4+x+1是GF(2)上的本原多项式。设α是4次本原多项式x4+x+1的根(α是本原元),则α是24-1=15级元素,α15=1,也就是说,元素α0=1,α1,α2,…,α14互不相同。因此,元素0,1,α,α2,…,α14是有限域GF(24)的全部16个元素。
由α4+α+1=0得α4=α+1。利用恒等式α4=α+1可以将αi表示为本原元α的3次多项式的形式,而这些多项式可以用其系数组成的4维矢量表示。例如,α4=α+1的4维矢量是1100;α5=α(α+1)=α2+α,其4维矢量是0110。因此,有限域GF(24)的元素的表示方法有α的幂次、α的多项式、α多项式的系数和多项式同余类等方法。在编码理论中主要使用前3种表示方法。表6.4给出了GF(24)的全部元素。
表6.4 用本原多项式x4+x+1构造的GF(24)的元素
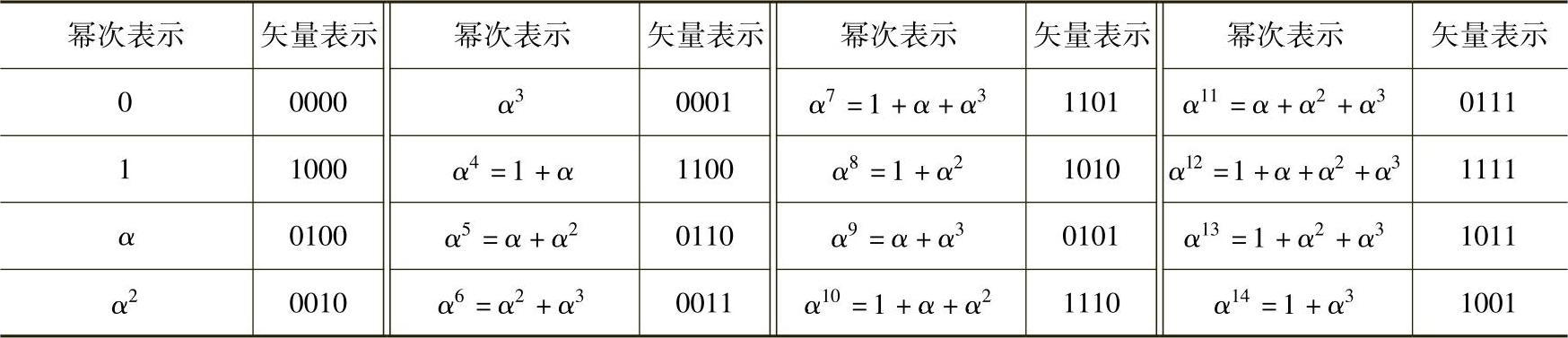
在进行有限域运算时,加法使用α的多项式或α多项式系数的表示法比较方便,乘法使用α的幂次的表示法比较方便。如α11+α8=(α+α2+α3)+(1+α2)=1+α+α3=α7,α11α8=α19=α4。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




