简化后：多项式同余类环

类似于整数模m同余类环的概念，可以引入多项式模g（x）同余类环的新概念，这就是多项式同余类环。为此先给出模多项式同余和多项式同余类的定义。

定义6.23 若两个GF（q）上的多项式a（x）和b（x）之差可以被另一个多项式g（x）整除，记为g（x）|（a（x）-b（x）），则称a（x）和b（x）关于模g（x）同余，记为a（x）≡b（x）（mod g（x））。

【例6.13】

设GF（2）上两个多项式a（x）=x⁴+x³+1，b（x）=x³+x²+x+1，计算

a（x）-b（x）=（x⁴+x³+1）-（x³+x²+x+1）=x（x³+x+1）

因此，a（x）≡b（x）（mod x³+x+1）。

定义6.24 给定GF（q）上的m次多项式g（x）（m＞0），将GF（q）上的全部多项式按模g（x）有相同的余式r（x）（∂r（x）＜∂g（x）或r（x）=0）进行分类，得到q^m个集合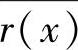，其中是由具有相同的余式的多项式组成，称为模g（x）同余类。

多项式同余和同余类的概念给出一种GF（q）上的多项式集合F_q[x]的分类方法，即将F_q[x]分成q^m个模g（x）同余类。任意多项式模g（x）的余数必为这q^m个多项式同余类之一。

【例6.14】(www.xing528.com)

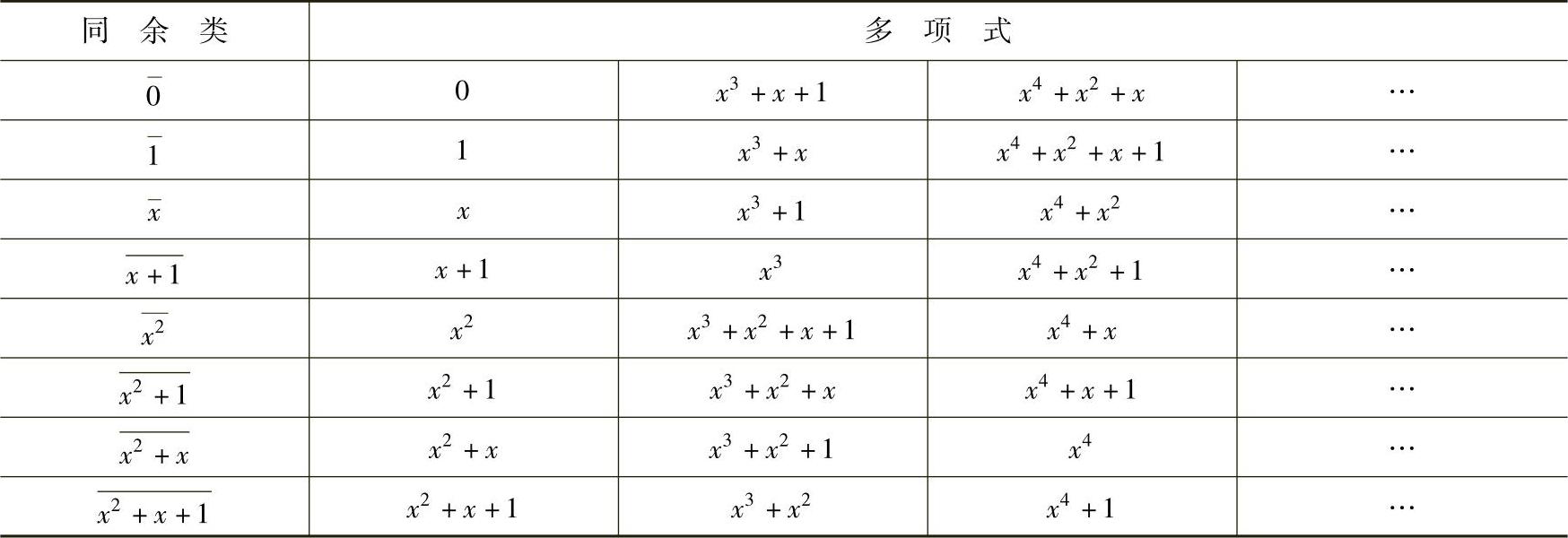
以GF（2）上的g（x）=x³+x+1为模，将F₂[x]划分为2³=8个模g（x）同余类，见表6.2。

表6.2 模x³+x+1划分的同余类

如同构造整数同余类环一样，也可以构造多项式同余类环。

定理6.12 给定GF（q）上的m次多项式g（x）（m＞0），则模g（x）的多项式同余类集合构成一个环，称为多项式同余类环。

定理6.13 给定GF（q）上的m次首一既约多项式g（x）（m＞0），则模g（x）的多项式同余类环是一个有q^m个元素的有限域GF（q^m）。

【例6.15】

表6.2的第一列全部元素集合组成GF（2）上的模g（x）=x³+x+1的多项式同余类环。又由于g（x）=x³+x+1在GF（2）上是首一既约的，则该多项式同余类环是一个有2³=8个元素的有限域。