1.群
定义6.5 非空集合G及其上定义一种运算“°”，若
1）满足封闭性，即对于任意a，b∈G，恒有a°b∈G。
2）满足结合律，即对于任意a，b，c∈G，恒有（a°b）°c=a°（b°c）。
3）存在单位元e，即对于任意a∈G，满足a°e=e°a=a。
4）对任意a∈G，都存在逆元a-1∈G，使a°a-1=a-1°a=e。则称G构成群（Group），记为〈G，°〉或G。
由定义6.5可知，群是一种只定义了一种代数运算的系统。
定义中的运算“°”若为普通加法，运算符“°”记为“+”，则a°b记为a+b，此时的单位元e记为0，它可以是数值零，也可以是零矢量或零矩阵等；而其逆元就是-a；G被称为加法群（或加群）。
若运算“°”表示普通乘法，运算符“°”记为“·”，则a°b记为a·b或简记为ab，此时的单位元e记为1，它可以代表数值1，也可以代表恒等变换或单位矩阵；而其逆元可以记为1/a；G被称为乘法群（或乘群）。
在加群中，对于任意a∈G，把n个a的运算记为a+a+…+a=na。在乘群中，对于任意a∈G，把n个a的运算记为a·a·…·a=an，规定a0=e。特别要注意的是，在上述表达式中a是群中的元素，n是整数。
若对于任意a，b∈G，有a°b=b°a，则G称为交换群（或Abel群）。无疑，加群总是交换群，但乘群却不一定，如矩阵乘法在一般情况下并不满足交换律。
【例6.5】
1）全体整数集合N对普通加法构成交换群，单位元是0，元素a的逆元是-a。全体整数集合N对乘法运算不构成群，因为没有乘法逆元。
2）全体实数集合R和有理数集合Q对加法构成交换群，单位元是0，元素a的逆元是-a；而全体非零实数集合R\0和全体非零有理数集合Q\0（集合符号R\0或Q\0表示从集合中去掉元素0以后的集合）对乘法运算构成交换群（因为0没有逆元），单位元是1，元素a的逆元是1/a。
3）全体n阶方阵集合对矩阵加法构成交换加群，单位元是零矩阵。全体非奇异的n阶矩阵集合构成乘群，单位元是n阶单位矩阵。
注：在数学上常用黑、正体的大写字母表示特定的集合，如整数集合N、有理数集合Q、实数集合R、复数集合C等。这样，相同的斜体符号还可以用于表达其他的量，例如，后面应用黑、斜体R表示环。
定义6.6 若整数a和b之差可以被正整数m整除，记为m（a-b）（竖线表示整除），则称a、b同余，记为a≡b（mod m）。
定义6.7 给定整数m（m＞1），将全部整数按模m有相同的余数进行分类，得到m个集合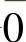
，
，…，
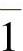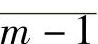，其中
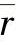（r=0，1，…，m-1）是由形如qm+r（q=0，±1，±2，…）的整数组成，称
，
，…，
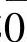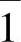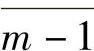为模m同余类，称Zm：{0，1，…，m-1}为模m同余类集合，一个同余类中任一数称为同类的数的同余。同余也称为剩余，同余类也称为剩余类。为了方便，也可以将同余类
，
，…，
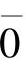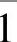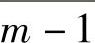简记为0，1，…，m-1，相应的模m同余类集合也简记为Zm：{0，1，…，m-1}。
同余和同余类的概念给出了一种全体整数集合Z的分类方法，即Z分成m个模m同余类。任意一个整数模m的余数必处于这m个同余类之一。
同余类之间可以定义加法和乘法运算，这种运算称为模运算，其定义为
可以证明，模m的同余类中，m个元素对于模m加法和乘法具有和整数相同的性质。
【例6.6】
1）{0，1}对模2加运算构成群，单位元是0，元素1的逆元是1。
2）模m同余类集合Zm：{0，1，…，m-1}对模m加法运算构成交换加群，对模m乘法运算构成交换乘群。
定理6.4 群G中单位元是唯一的，每个元素的逆元也是唯一的。
定理6.5 若a，b∈G，则（a°b）-1=b-1°a-1。
推论6.1 若a，b，c，…，f∈G，则（a°b°c°…°f）-1=f-1°…°c-1°b-1°a-1。
定理6.6 给定G中任意两个元素a和b，则方程a°x=b和y°a=b在G中有唯一解。
推论6.2 群G中的消去律成立，即由a°x=a°y或x°a=y°a推得x=y。
定义6.8 群中元素的个数称为群的阶；若群的阶为无限则称为无限群，否则称为有限群。
定义6.9 若存在a∈G，使得G中每个元素都是a的某次幂，即an（n是整数），则G称为循环群。此时称该循环群由a生成，a是该群的生成元。记G=（a）或G（a）。
【例6.7】
1）全体整数集合Z关于加法构成循环群，1是生成元。因为该群有无限多个元素，故是一个无限循环群。
2）若a0=1，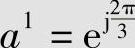
，
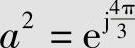，a3=ej2π=a0=1，
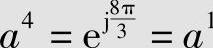，…是一个循环的交换乘群。该群只有3个元素，表示为{1，a，a2}，1是乘法单位元。该群是有限循环群。
定义6.10 使an=1的最小正整数n称为元素a的级。
有限循环群G（a）有以下性质：
性质6.1 若a是n级元素，群G（a）中的n个元素a0=1，a1，a2，…，an-1均互不相同，且由a的一切幂次生成的元素都在G（a）的集合中。
性质6.2 若a是n级元素，则am=1的充要条件是n整除m。
性质6.3 若a，b∈G，a是n级元素，b是m级元素，且n和m互素，则ab的级为nm。
性质6.4 若a为mn级元素，则am元素的级为n。
2.环和域(www.xing528.com)
定义6.11 非空元素集合R中定义了加法和乘法两种运算，若满足下述公理：
1）R中全体元素构成交换加群，加法单位元为0，称a的加法逆元为负元，记为-a。
2）乘法运算满足封闭性。
3）乘法满足结合律。
4）加法和乘法之间满足分配律。则称R是环（Ring），记为〈R，+，.〉，简记为R。
由定义6.11知，环是一种定义了称为加法和乘法的两种代数运算的系统。
在环中加法运算构成加群，因此，集合中必含有加法单位元；而乘法运算并没有要求构成乘群，因此，也没有要求一定含有乘法单位元。若在一个环中无乘法单位元，此时当然也无逆元。对于有乘法单位元的环，称这类环为单位元环。若环关于乘法满足交换律，即对任意a，b∈R，恒有ab=ba，则称此环为交换环。
【例6.8】
1）全体整数集合Z关于普通加法和普通乘法运算构成交换环。全体偶数集合构成环，且是没有乘法单位元的环。
2）模m同余类集合Zm：{0，1，…，m-1}关于模m同余类加法和乘法构成交换环，称Zm为模m同余类环。
3）全体实系数多项式集合R[x]构成环。
4）全体n阶方阵集合构成环。
定义6.12 设a，b∈R，a≠0，b≠0，若ab=0，则称a、b为零因子；含有零因子的环称为有零因子环；不含零因子的环称为整环。
【例6.9】
模6同余类集合Z6：{0，1，2，3，4，5}有6个元素。因为2≠0，3≠0，但2×3=6=0（mod 6）。所以，2和3是同余类环Z6的零因子，该环是有零因子环。
可以证明，若m是合数，则模m同余类环Zm是有零因子环；若m是素数，则模m同余类环Zm是整环。
定义6.13 非空集合F中定义了加法和乘法两种运算，若满足下述公理：
1）F中全体元素构成交换加群，加法单位元为0，称a的加法逆元为负元，记为-a。
2）F中全体非零元素构成交换乘群，乘法单位元为1。
3）加法和乘法之间满足分配律。则称F是域（Field），记为〈F，+，.〉或F。
由定义6.13知，域也是一种定义了称为加法和乘法的两种代数运算的系统，是一种交换的、有乘法单位元的、有乘法逆元的、没有零因子的环。
对于环或域均有对于任意a，b∈R或a，b∈G，把a+（-b）记为a-b，并由此引入了减法的概念。因此在研究代数结构时，一般仅研究加法运算。
非空集合是否构成域，可以根据定义6.13逐条验证，但最关键的是封闭性与乘法逆元。
定义6.14 域中元素的个数称为域的阶。若域中元素有无限多个，则称为无限域；若域中元素个数有有限多个，则称为有限域或Galois（伽罗华）域。
通常，含有q个元素的有限域记为GF（q）或Fq。
【例6.10】
1）全体有理数集合Q、全体实数集合R和全体复数集合C对普通加法和乘法运算分别构成有理数域、实数域和复数域。它们都是无限域。
2）{0，1}对模2加法和模2乘法运算构成二元域，记为GF（2）或F2。
3）模m同余类的集合Zm，无论m是素数还是合数，均构成交换加群。而整数模6同余类集合Z6不能构成域，这是因为其非零元素的全体不能构成交换乘群（参见例6.9，2和3没有乘法逆元）。
定理6.7 设p为素数，则集合Zp：{0，1，…，p-1}在模p加法和乘法运算下构成p阶有限域GF（p）或Fp。
3.子群和陪集
定义6.15 若群G的非空子集H对于G中的代数运算构成群，则称H为群G的子群。
定理6.8 群G的非空子集H为G的子群的充要条件是，对于任意h1，h2∈H，恒有h1°h2-1∈H。
【例6.11】
全体偶数集合构成的加群是全体整数集合Z所构成的加群的一个子群。全体整数集合Z构成的加群是全体有理数集合Q所构成的加群的一个子群。
定义6.16 设H是群G的一个子群。任一元素g∈G，h1，h2，…是H中的所有元素，称g°H={g°h1，g°h2，…}为子群H在群G中的一个左陪集，称H°g={h1°g，h2°g，…}为右陪集。陪集中左面第一个元素称为陪集首。H的第一个元素规定为G的单位元。
在编码中应用的是交换群，故左陪集等于右陪集，简称为陪集。利用子群和陪集的概念，把G中的元素按子群H划分成等价类。设G中的元素是g1，g2，…，则陪集的划分见表6.1。
表6.1 陪集划分
有限群G按子群H划分成有限个互不相交的陪集，各个陪集的元素数目相同，即等于子群H的阶。将群G进行陪集划分是一种完备的划分方法，G中所有元素均在此阵列中，且不重复出现。若G的阶为N，H的阶为n，则应有N=kn，其中k为整数。
类似于子群的概念，也可以定义子环和子域。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
