信道编码的分类及特点分析

在深入研究信道编码之前，先从信道编码的结构特点、性能与构造方法等多角度，对信道编码进行分类。

（1）按纠正错误方式分类

按纠正错误方式，信道编码分为自动发现错误的检错码，或者不仅能发现错误而且能纠正错误的纠错码，或者纠正删除错误的纠删码。但是，这三类码之间没有明显的区分。事实上，任何一类码按照译码方法的不同，均可以作为检错码、纠错码和纠删码来使用。

（2）按编码规则的局限性分类

按编码规则的局限性，信道编码分为分组码和卷积码。

若编码的规则仅局限在本码组之内，即本码组的校验元仅与本码组的信息元相关，称这类码为分组码。若本码组的校验元不仅与本码组的信息元相关，而且还与本码组相邻的前v个码组的信息元相关，则这类码称为卷积码。

在分组码中，待编码的信息组由k个码元组成。信道编码器对每个信息组独立地进行编码，附加的n-k个码元仅与该信息组的k个码元有关。编码器输出长度为n的码字，又称码组。所有的码字集合称为（n，k）分组码。对于有k个信息元和n-k个校验元的分组码用（n，k）表示，其编码速率（或码率）定义为R=k/n。由于分组码的每个码字只取决于相对应的信息组，所以，编码器是无记忆的，可以用组合逻辑电路来实现。

卷积码编码器是对k₀个码元的信息组进行编码，输出长为n₀个码元的码字。但每个码字可以附加的校验元，不仅与此时刻输入到编码器的信息组有关，还与此时刻相邻的前v个信息组有关。因此，编码器应含有v级存储器，存储前v个时刻中输入到编码器的每组k₀个信息元。所以，卷积码编码器是有记忆的，必须用时序逻辑电路来实现。v称为卷积码的编码存储，v+1称为卷积码的约束度。卷积码常用（n₀，k₀，v）表示，其编码速率定义为R=k₀/n₀。

（3）按编码规则的约束关系分类

按编码规则的约束关系，信道编码分为线性码和非线性码。

若码字的码元之间满足线性方程组的约束关系，则称该类码为线性码。相应地，若码字的码元之间不满足线性方程组的约束关系，则称该类码为非线性码。例如，电信中常用的等比码是非线性码。非线性码的分析比较困难，实现较为复杂，本书主要讨论线性码。

（4）按编码后码字的信息组的结构分类

按编码后码字的信息组的结构，信道编码分为系统码和非系统码。

在系统码中，每个码字的k个（或k₀个）信息元以不变的形式出现在码组中，而非系统码不具有这种结构性质。

（5）按纠正错误的类型分类(www.xing528.com)

按纠正错误的类型，信道编码分为纠随机错误码、纠突发错误码和纠同步错误码，以及既能纠随机错误又能纠突发错误的码。

（6）按码字中每个码元的取值分类

按码字中每个码元的取值，信道编码分为二元码（二进制码）和q元码（q进制码）。q元码中，通常取q=p^m，其中，p为素数，m为正整数。

（7）按对每个信息元的保护能力是否相等分类

按对每个信息元的保护能力是否相等，信道编码分为等保护纠错码和不等保护纠错码。

除非特别声明，下面讨论的纠错码均指等保护纠错码。

（8）按码字的循环结构分类

按码字的循环结构，信道编码分为循环码和非循环码。

在循环码中，任一码字循环移位得到的仍是该码字集合中一个码字。而在非循环码中，一个码字的循环移位后不一定是该码的一个码字。

（9）按构造码的数学方法（或称数学结构）分类

按构造码的数学方法，信道编码分为代数码、几何码和算术码。

为清楚起见，上述的大部分信道编码的分类可以用图6.5来表示。

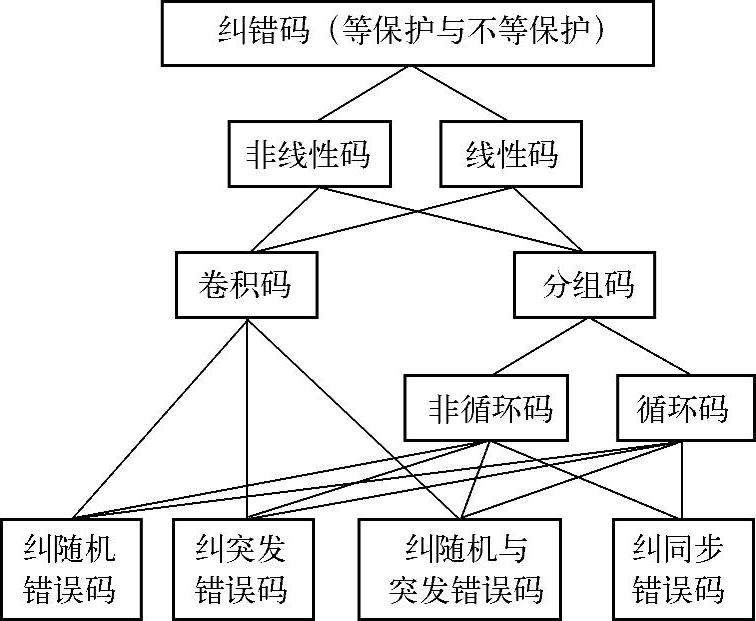
图6.5 信道编码的分类