通信的过程并不是信息传输到信道输出端就结束了,还要经过译码过程才能到达信宿。除信道的转移特性外,译码过程和译码规则对系统的错误概率影响很大。下面举例说明信道转移概率和译码规则对通信系统的错误概率是有影响的。
【例6.1】
二元对称信道如图6.1所示,信道的输入符号为等概率分布。如果译码规则为:
1)接收到“0”时译码器输出“0”,接收到“1”时译码器输出“1”,则错误译码概率为
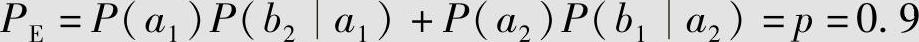
2)反之,接收到“0”时译码器输出“1”,接收到“1”时译码器输出“0”,则错误译码概率为
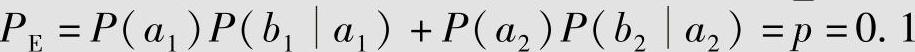
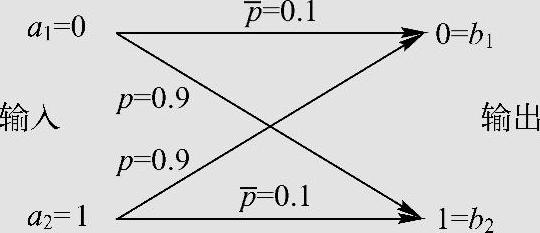
图6.1 二元对称信道(BSC)
从例6.1中可见,译码规则2)优于译码规则1),且错误译码概率既与信道统计特性有关,也与译码规则有关。
定义6.1 设信道的输入随机变量X的值域为符号集A:{a1,a2,…,ar},输出随机变量Y的值域为符号集B:{b1,b2,…,bs},若对每一个输出符号bj,都有一个确定的单值函数F(bj),使bj对应于唯一的一个输入符号ai,称这样的函数为译码规则,记为
F(bj)=ai,i=1,2,…,r且j=1,2,…,s (6.1)
对于有r个输入、s个输出的信道,输出bj可以对应r个输入中的任何一个,所以译码规则共有rs种。显然,这些译码规则的性能是有差异的。
【例6.2】
设某信道输入符号集为A:{a1,a2,a3},输出符号集为B:{b1,b2,b3},转移概率矩阵为

根据此信道矩阵,可以设计两个译码规则如下:
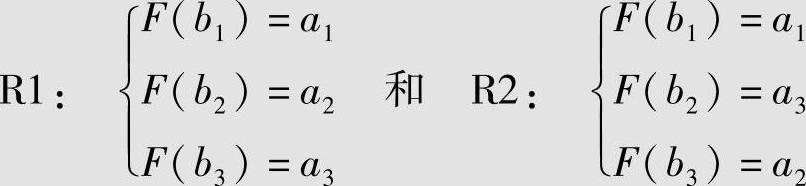
例6.2中,r=s=3,所以可以设计出多达rs=27种译码规则。但这些译码规则中,只有很少的规则是性能优良的。因此,需要从理论上解决选择最佳的译码规则的一般方法。一个很自然的准则就是使平均错误概率最小。
在确定译码规则F(bj)=ai(i=1,2,…,r;j=1,2,…,s)后,若信道输出端接收到符号bj,则一定译成ai。如果发信端发送的确实就是ai,就是正确译码;反之,若发信端发送的不是ai,就认为是错误译码。于是,给出如下定义:
定义6.2 收到符号bj条件下,译码的条件正确译码概率为

而条件错误译码概率为
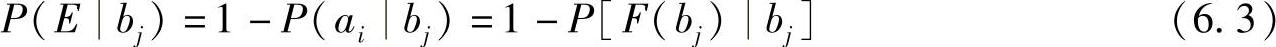
式中,E表示除了F(bj)=ai以外的所有输入符号的集合。译码后的平均错误译码概率为

显然,最佳译码规则就是使平均错误译码概率PE为最小的译码规则。由于式(6.4)右边是非负项之和,所以可以选择译码规则使每一项为最小,则所得PE为最小。因为P(bj)与译码规则无关,所以只要设计译码规则F(bj)=ai使条件错误概率P(E|bj)最小,也就是要使P[F(bj)|bj]最大。这就是最大后验概率准则。
定义6.3 选择译码函数F(bj)=a*(a*∈A;bj∈B),使之满足条件
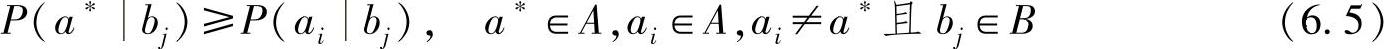
这称为最大后验概率译码准则,又称为最小错误概率准则。
因为一般是已知信道的前向概率P(bj|ai)和输入符号的先验概率P(ai),所以根据贝叶斯公式,式(6.5)可以写成
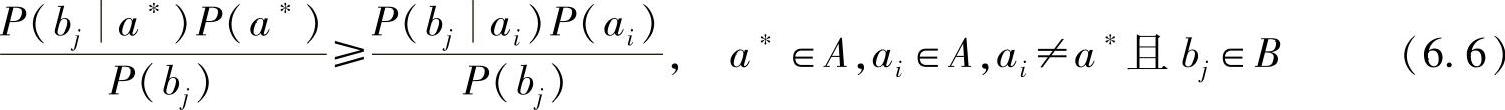
一般P(bj)≠0。这样,最大后验概率译码准则就可以表示为:选择译码函数F(bj)=a*,使其满足
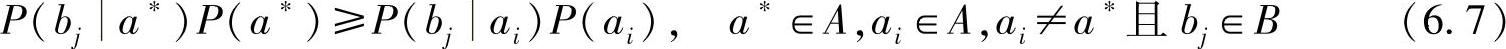
当输入符号的先验概率P(ai)相等时,式(6.7)又可以写成P(bj|a*)≥P(bj|ai)。因此,可以定义一个有条件最佳的最大似然译码准则。
定义6.4 选择译码函数F(bj)=a*(a*∈A;bj∈B),使之满足条件

这称为最大似然译码准则。
根据最大似然译码准则可以直接从信道转移概率矩阵中选定译码函数:
当收到bj后,译成信道转移概率矩阵P中第j列中最大的转移概率所对应的ai。
最大似然译码准则本身不依赖于先验概率P(ai),当先验概率为等概率分布时,它与最大后验概率译码准则是等价的,可以使平均错误概率PE达到最小。如果先验概率不相等或不知道时,仍可以采用这个准则,但不一定能使PE最小。
根据译码规则和式(6.2)~式(6.4),计算平均错误译码概率为
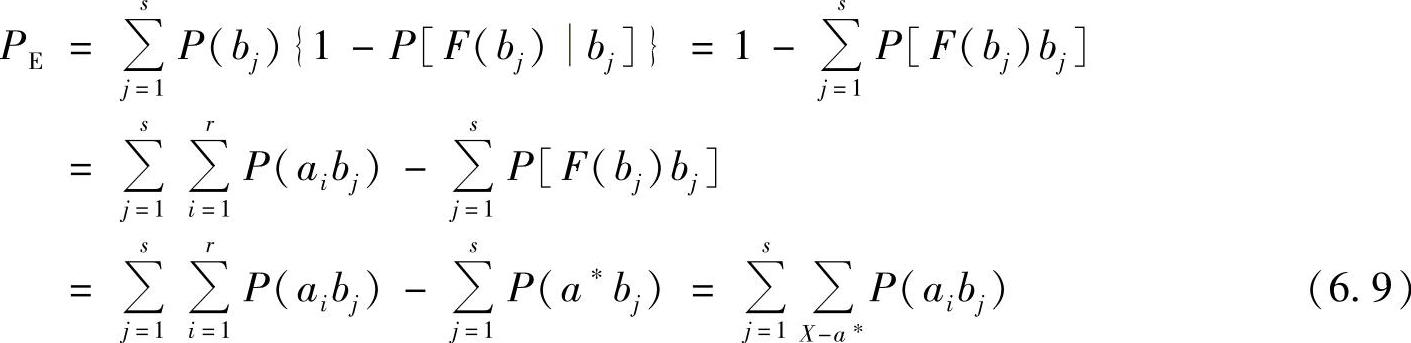
而平均正确译码概率为
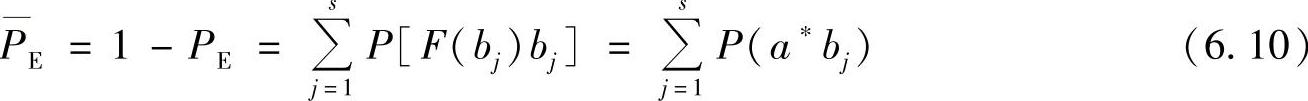
式(6.9)中,符号X-a*表示集合A中除F(bj)=a*以外的所有元素。式(6.9)表示对联合概率矩阵[P(aibj)]中除P(a*bj)以外的所有(r-1)s个元素求和。
式(6.9)又可以写成(https://www.xing528.com)

式(6.11)的平均错误概率是在联合概率矩阵[P(ai)P(bj|ai)]中,先求每列除去F(bj)=a*所对应的P(a*bj)以外所有元素之和,然后再对各列求和。当然,也可以在[P(ai)P(bjai)]中先对行i求和,除去译码规则中F(bj)=a*所对应的P(aibj)(j=1,2,…,s),然后再对各行求和。因此,式(6.11)还可以写成

式中,令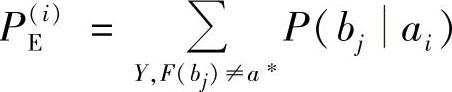 。PE(i)就是某个输入符号ai传输所引起的错误概率。
。PE(i)就是某个输入符号ai传输所引起的错误概率。
如果先验概率P(ai)为等概率分布,即P(ai)=1/r,则由式(6.11)得
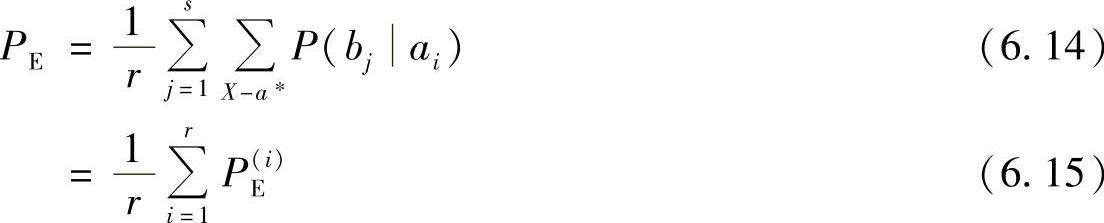
式(6.14)表明,在等先验概率分布情况下,译码错误概率可以用信道矩阵中的元素P(bjai)的求和来表示。式(6.14)求和是除去每列中对应于F(bj)=a*的那一项后,先对列求和,然后求各列之和。而式(6.15)是由式(6.13)求得,它是先对行求和,然后求各行之和。式(6.14)和式(6.15)只是求和表达式的不同表述。
【例6.3】(续例6.2)
当输入为等概率分布时,求例6.2中两种译码规则对应的平均错误译码概率。
解 当输入为等概率分布时,译码规则R2就是最大似然译码准则。
由式(6.14)计算两种译码规则所对应的平均错误译码概率分别为
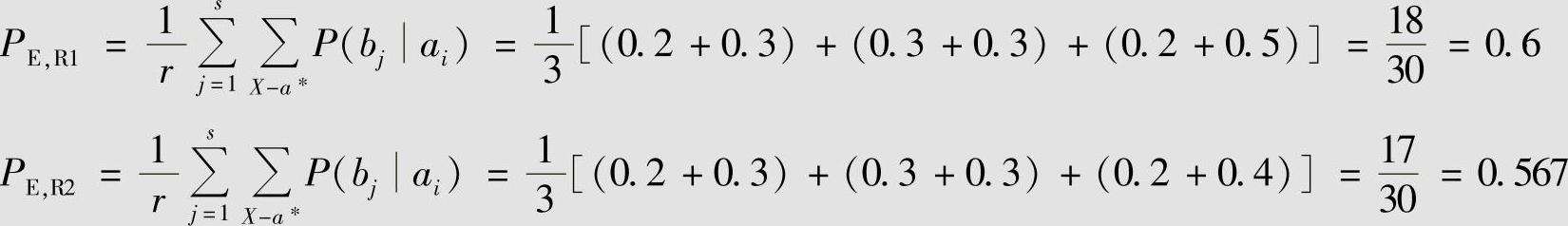
可见PE,R2≤PE,R1,所以在输入等概率时最大似然译码准则可以使信道平均错误概率最小。
【例6.4】(续例6.2)
当输入为不等概率分布,且为P(a1)=P(a2)=0.25,P(a3)=0.5时,求例6.2中两种译码规则和采用最小错误概率准则对应的平均错误译码概率。
解 先计算联合概率矩阵[P(ai)P(bj|ai)]为

根据最小错误概率译码准则,由式(6.5)得最小错误概率译码准则下的译码函数为
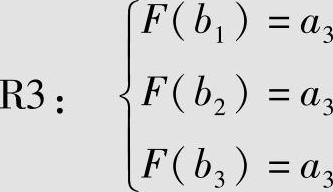
再由式(6.9)计算例6.2中两种译码规则和译码规则R3所对应的平均错误译码概率分别为

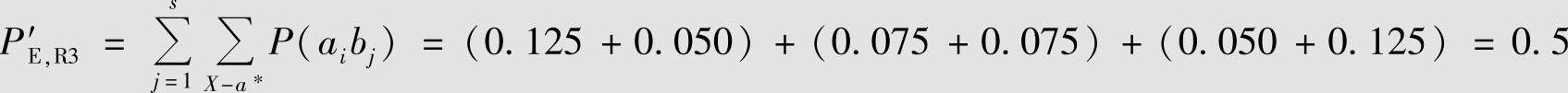
可见,输入非等概率分布时最大似然译码准则的平均错误译码概率不是最小的。
由例6.3和例6.4可以看出,当输入非等概率分布时,最大似然译码准则的平均错误译码概率已从等概率分布时PE,R2=0.567变成例6.4分布时的P′E,R2=0.6;且在例6.4的输入分布时,最佳译码(最小错误概率译码)的平均错误译码概率为P′E,R3=0.5。
译码时发生错误是由信道中的噪声引起的,而信道噪声的影响使在收信端收到输出符号Y后对发信端发送的符号仍然存在不确定性。因此,平均错误译码概率与信道疑义度存在着一定的关系,这个关系就是Fano(费诺)不等式。
定理6.1(Fano不等式)平均错误译码概率PE与信道疑义度H(XY)满足以下关系:
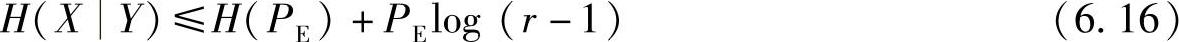
证明 由式(6.10)和式(6.9)得
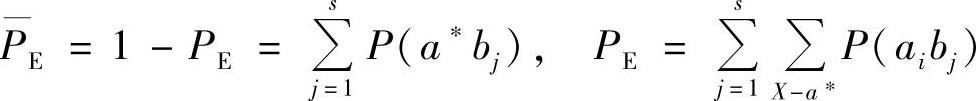
那么
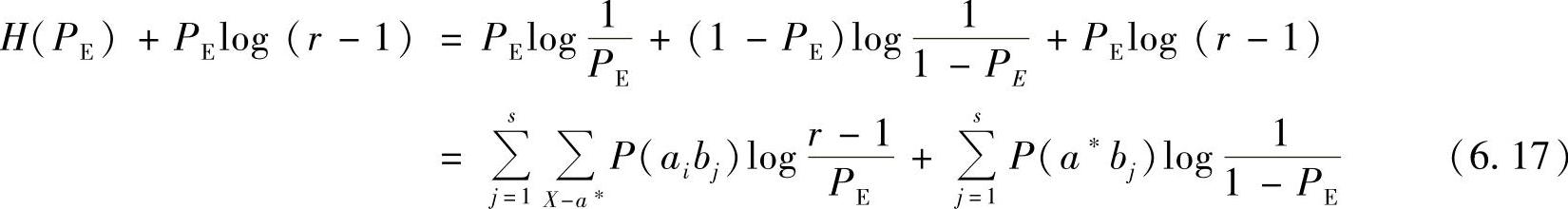
而信道疑义度
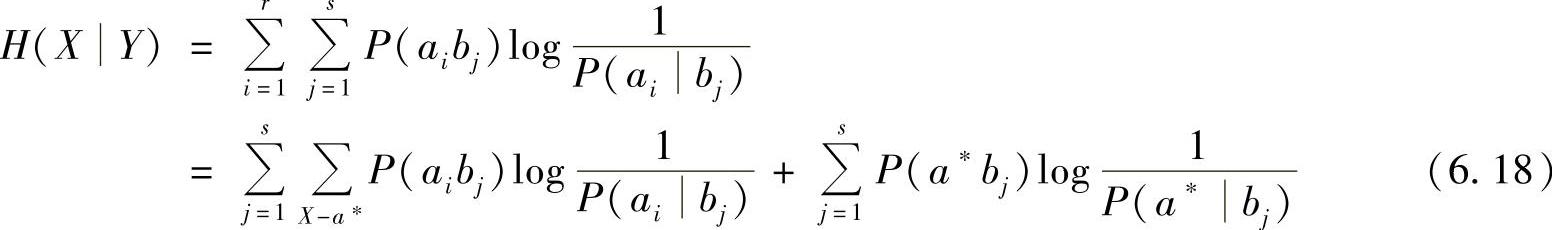
联合式(6.17)和式(6.18)得
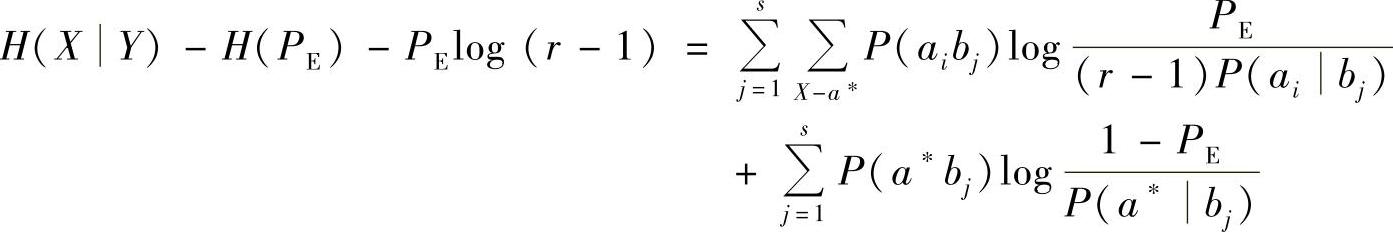
利用不等式ln x≤x-1(x>0;仅当x=1时等式成立),得
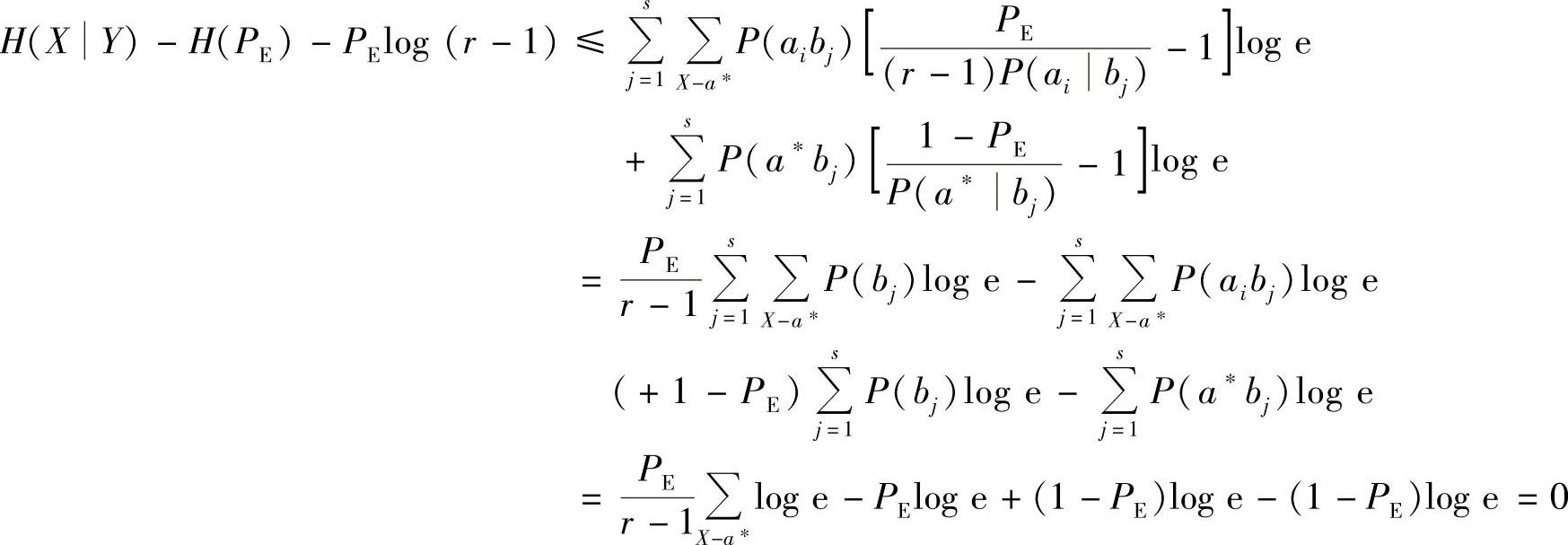
故证得Fano不等式(6.16)。
【证毕】
虽然PE与译码规则有关,但是不管采用什么译码规则,Fano不等式(6.16)都是成立的。Fano不等式表明,接收到Y后关于X的平均不确定性可以分为两部分:
1)H(PE)是指接收到Y后是否产生错误的不确定性。
2)PElog(r-1)是当错误PE发生后,判断是哪个输入符号造成错误的最大不确定性,是r-1个符号不确定性的最大值与PE的乘积。
若以H(XY)为纵坐标,PE为横坐标,函数H(PE)+PElog(r-1)随PE变化的曲线如图6.2所示。PE的最大值为1,这时H(XY)=log(r-1);当PE=(r-1)/r时,H(XY)=logr,取到最大值。

图6.2 Fano不等式曲线图
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




