如何选择最佳变换编码方法？

变换是一个广泛的概念。在通信与信息处理系统中，常希望把信号进行变换以达到某种目的。信源编码实际上就是一种变换，使之能在信道中更有效地传输。这里讨论的变换是数学意义上一一对应的变换。变换编码就是经变换后的信号的样值能更有效地编码，也就是通过变换来解除或减弱信源符号间的相关性，再将变换后的样值进行量化，或采用对于独立信源符号的编码方法，以达到压缩码率的目的。

1.变换的一般原理

设函数f（t）（0＜t＜T）满足

则函数f（t）可以用完备正交函数系来表征。

再设完备正交归一函数系φ（i，t）（i=0，1，2，…），该函数的正交性和归一性表示如下：

利用φ（i，t）（i=0，1，2，…）的级数表示方法，可以把函数f（t）展开为

式中，a_i（i=0，1，2，…）是待定系数，可以用有限项逼近时的均方误差最小准则来确定。即

利用函数φ（i，t）的正交性式（5.72）和归一性式（5.73），可得

如果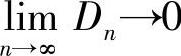，则称上述正交函数系是完备的，此时式（5.74）才成立。否则，正交函数系是不完备的，因而式（5.74）也就不成立。

与欧氏空间类比，可见式（5.74）实际上就是把函数矢量分解成各坐标分量，式（5.75）相当于内积运算，把函数f（t）投影到φ（i，t）（i=0，1，2，…）上。

通过上述变化，把函数f（t）变换成一系列离散的系数a_i（i=0，1，2，…）。若已给出这些系数，就可以用式（5.74）恢复函数而不产生误差。所以，这种变化是可逆的。如果只取有限个系数，恢复时就会引入一定的误差。

最常用的、最熟悉的傅里叶变换是一种完备正交归一函数系。从解除相关性的意义上说，傅里叶变换不是一种很好的变换。要有效地解除相关性，正交函数系必须根据信源的相关函数来选择。

以均方误差最小准则来推导，可以得到一种最佳的正交变换，称为K-L变换（Karhunen-Loeve Transform）。这个变换可以使变换后的随机变量之间互不相关。一般认为K-L变换是压缩编码的最佳变换，评价其他变换时，常与它进行比较。K-L变换的最大缺点是计算复杂，除了需要测定相关函数和解积分方程外，变换时的运算也十分复杂，尚无快速算法可用。(www.xing528.com)

以上的变换是在时间上连续的信源输出x（t）中取一段（0，T）进行积分运算，得到一系列系数a_i（i=0，1，2，…），截取有限的n个系数a_i（i=0，1，…，n-1），并对各a_i进行量化，达到信源编码的目的。这种方法在实际编码时较少应用，因为积分运算一般地说是比较困难的，而且除了量化各系数将引入失真外，截取有限个系数也会引入失真。要保持失真在某一限度内，可能量化级数要有一定的增多，这将使码率有所上升。

另一种方法是先对信源输出x（t）取样，得到一系列离散值x（i）（i=0，1，2，…），然后取N个样值形成一个N维矢量，对矢量用矩阵进行变换，成为另一域内的N维矢量，以解除或减弱矢量内各分量的相关性。再对后一个分量进行标量量化或对矢量进行矢量量化来完成信源编码。此时的变换已不用积分运算而是矩阵运算。若变换所用的矩阵选得恰当，就可以达到压缩码率的要求。用矩阵来变换常称为离散变换。

其实取样也是一种把连续函数变换成时间上离散的一系列值的变换。此时变换所用的正交函数是单元脉冲函数δ（t-i，τ）（i=0，1，2，…），τ是取样间隔。单元脉冲函数系的正交性和完备性是明显的；但这里已不是截取一段（0，T）信源输出而是连续进行取样运算。要使变换能一一对应，也就是能无失真地恢复原来的连续函数，信源输出必须是限频的。根据奈奎斯特采样定理，若信源输出信号的最高频率是f_m，则取样间隔τ必须小于1/2f_m，才能使变换可逆。

2.离散傅里叶变换

前面提到的傅里叶变换具有其相应的离散变换的形式，即离散傅里叶变换（DFT）。设信源输出x（t）的一个N长取样序列为x（0），x（1），…，x（N-1），其对应的离散傅里叶变换的频域序列为X（0），X（1），…，X（N-1），则离散傅里叶变换和反变换表达式分别为

经离散傅里叶变换后的输出的频域序列X（0），X（1），…，X（N-1）中，各分量间的相关系数将与原输入过程的相关函数有关。一般来说，输入过程的相关系数越接近1，输出各分量间的相关函数越小，也就是说，离散傅里叶变换对强相关的信源是有效的。此外各输出分量的方差将不同，有大有小，即经变换后能量有所集中，这对压缩码率是有利的。

3.离散余弦变换

DFT虽然有快速算法，可以减少计算量，但还是需要复数运算，使得其运算量偏大，这在工程应用中是不方便的。为了克服这些缺点，在寻求快速算法的同时，基于DFT构造了一种实数域变换——离散余弦变换（DCT）。由于离散余弦变换的性能正好符合人类语音和图像信号的特点，因此在这个意义上说，常常认为离散余弦变换是接近K-L变换性能的准最佳变换。

设信源输出x（t）的一个N长取样序列为x（0），x（1），…，x（N-1），其对应的离散余弦变换的频域序列为X（0），X（1），…，X（N-1），则离散余弦变换和反变换表达式分别为

离散余弦变换是使用最广泛的变换编码技术，已经应用于很多编码标准中，如电视电话/会议视频编码标准H.261和H.263；静态图像编码标准JPEG；视频编码标准MPEG1、MPEG2、MPEG4等。

还有很多离散变换，如正、反变换矩阵都相同的离散哈尔变换和离散沃尔什变换；由有限维正交矢量系导出的广泛用于电视信号编码的斜变换和多重变换；可以把信号分割成多个窄带以解除或减弱信号样值间相关性的子带编码和小波变换等。在实际应用中，需要根据信源特性来选择变换方法以达到解除相关性、压缩码率的目的。另外还可以根据一些参数来比较各种变换方法间的性能优劣，如反映编码效率的编码增益、反映编码质量的块效应系数等。当信源的统计特性很难确知时，可以用各种变换分别对信源进行变换编码，然后用实验或计算机仿真来计算这些参数。