预测编码理论与方法：解除序列相关性的常用措施

由信息论可知，对于相关性很强的信源，条件熵可以远小于无条件熵。因此，人们常采用尽量解除相关性的办法，使信源的输出转化为独立序列，以利于压缩码率。解除相关性的常用措施是预测和变换，其实质都是进行序列的一种映射。一般来说，预测编码有可能完全解除序列的相关性，但必须确知序列的概率特性。变换编码一般只能解除矢量内部的相关性，但它可以有许多可供选择的变换方法，以适用不同的信源特性。

下面介绍预测编码的一般理论与方法。

预测就是从已收到的符号来提取关于未收到的符号的信息，从而预测其最可能的值作为预测值；并对它与实际值之差进行编码，达到进一步压缩码率的目的。由此可见，预测编码是利用信源的相关性来压缩码率的，对于独立信源就没有预测的可能了。

设信源序列为x₁，x₂，…，x_r，x_r+1，…。r阶预测就是由x₁，x₂，…，x_r来预测x_r+1。令预测值为

x′_r+1=f（x₁，x₂，…，x_r） （5.68）

式中，f是待定的预测函数。要使预测值具有最小均方误差（此时的预测称为最佳预测），必须确知r+1个变量（x₁，x₂，…，x_r，x_r+1）的联合概率密度函数，这在一般情况下是困难的。因而，常用线性预测的方法来达到次最佳的结果。线性预测就是预测函数为各已知信源符号的线性函数，即x_r+1的预测值是前几个符号值的线性组合，其预测函数为

并求均方误差D=E[（x_r′₊₁-x_r+1）²]最小时的各a_i（i=1，2，…，r）值。为此，令(www.xing528.com)

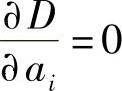，得

式（5.70）是一组有r个未知参数a_i（i=1，2，…，r）、由r个独立方程组成的线性方程组。当已知信源各符号之间的相关函数后即可进行求解。

最简单的预测是令x′_r+1=x_r，这可以称为零阶预测，常用的差值预测就属这一类。高阶线性预测已在语音编码，尤其是声码器中广泛采用。如果信源是非平稳的或非概率性的，无法获得确切和恒定的相关函数，此时可以采用自适应预测的方法。有关预测参数a_i（i=1，2，…，r）的具体求解方法请参考文献[26]。

利用预测值来编码的方法可以分为两类：

一类是对实际值与预测值之差进行编码，也叫差值编码。常用于相关性强的连续信源，也可以用于离散信源。在连续信源的情况下，就是对此差值量化或取一组差值进行矢量量化。由于相关性很强的信源可以较精确地预测待编码的值，使得差值的方差远小于原来的方差。所以，在同样失真要求下，量化级数可以明显地减少，从而较显著地压缩了码率。对于离散信源也有类似的情况。

另一类方法是根据差值的大小，决定是否需传送该信源符号。例如，可以规定某一容许值，当差值小于该容许值时可以不传送。对于连续函数或相关性很强的信源序列，常有很长一串符号可以不传送而只需要传送这串符号的个数，这样就能大量地压缩码率。这一类方法一般是按信宿要求设计的，也就是失真应能满足信宿需求。