量化编码的信息率失真函数及其界限

1.量化编码的作用

连续信源限失真编码的主要方法是量化，量化就是把连续信号（又称为模拟信号）变换为离散信号的过程。所以量化也可以称为数字化，量化后的信号称为数字信号。这种转换必将引入失真（或误差）。

量化的目标是使这种失真尽量小。常用的量化方法有标量量化和矢量量化。标量量化是指每次只量化一个模拟样本值，故又称为零记忆量化。矢量量化是把多个模拟样本值联合起来形成多维矢量后再进行量化。

2.标量量化

设连续信源的模拟样本值x（t）的值域为（a，b），即a＜x（t）＜b，a可以为-∞，b可以为∞。所以，上述假设不失一般性。

标量量化就是将（a，b）区间分成n个互不重叠的小区间（一般称n为量化级数），每个区间内确定一个量化值y_i，若各区间的端点为a_i-1和a_i，则必有

a₀≤y₁≤a₁≤y₂≤a₂≤…a_n-1≤y_n≤a_n （5.58）

当x（t）的值处于（a_i-1，a_i]（或[a_i-1，a_i））区间上，则将其量化为该区间的量化值y_i，这样就实现了标量量化。显然，量化将引入量化误差（或量化噪声），该误差可以表示为

ε_i=x-y_i （5.59）

最佳标量量化就是在确定n值后，在最佳准则（一般是假定某种平均量化误差为最小）下，确定各a_i和y_i的值。此时，信息传输率为R=log n。

在一般情况下，最佳标量量化是比较难解的，这时可以采用递推算法获得近似解。从理论上说，只要递推次数足够多，就可以得到相当精确的解，但是计算量很大，收敛速度不快。在某些特殊情况下，可以采用求解析表达式方法。下面举一个有解析解的例子。

设x（t）在（0，L）区间内均匀分布，即x（t）的概率密度函数为

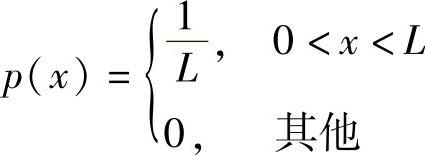
先计算x（t）的方差σ²和平均偏差1/λ。根据定义可得

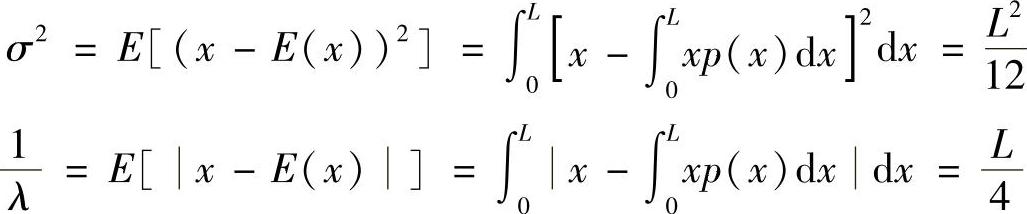
当量化级数为n时，可以将（0，L）区间均匀分割成n个小区间，小区间的宽度（或量化间隔、量化级差）为Δ=L/n，以每个小区间的中点作为量化值，即

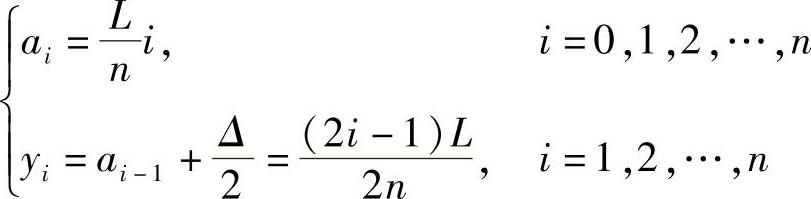
则平均失真为

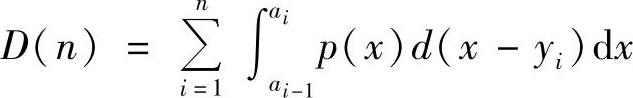
当失真函数选用平方误差失真时，量化的平均误差为

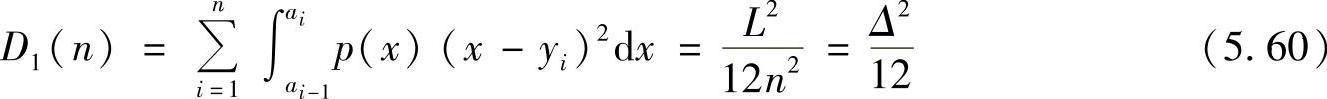
因此，可以解得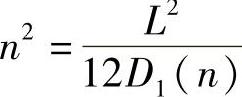，此时的信息传输率R₁=log n可以进一步写成

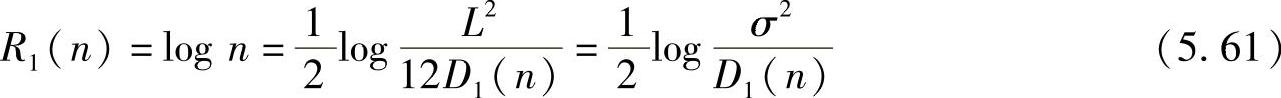
当失真函数为绝对误差失真时，量化的平均误差为

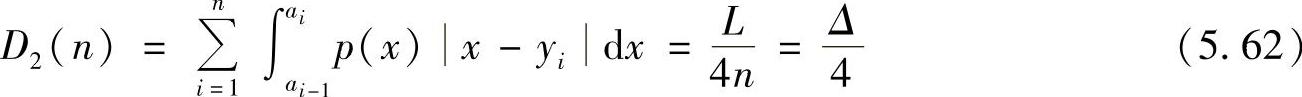
因此，可以解得，此时的信息传输率R₂=log n可以进一步写成

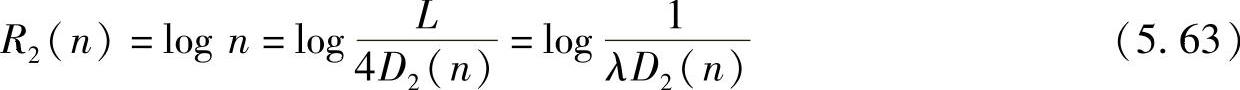
比较式（5.60）和式（5.62）可见，上述两种情况定义的平均失真虽然不同，但结论是相同的，即对于标量量化而言，量化间隔Δ越小，平均失真就越小，量化级数n就越大，所需要的信息传输率也就越大。

信息论中已经证明：

对于平方误差失真，当方差一定时，正态分布的信息率失真函数R（D）恒大于其他分布时的R（D）；

对于绝对误差失真，当平均偏差一定时，负指数分布的信息率失真函数R（D）恒大于其他分布时的R（D）。

可以证明，式（5.61）和式（5.63）的右侧分别是正态分布和负指数分布的信息率失真函数，所以，即使在最佳标量量化的情况下，仍未能达到信息率失真函数所规定的界，而且量化以后的各量化值y_i的概率是相同的，等于1/n，因而倘若x（t）的各连续符号相互独立，也就不能再用无损编码进一步压缩码率。由此可见，最佳标量量化在这里也不是最佳限失真编码。

3.矢量量化

要想得到性能好的编码，仅采用标量量化是不可能的。在前面的最佳编码中可以看到，将离散信源的多个符号联合编码可以提高效率，连续信源也是如此。当把多个连续信源符号联合起来就形成了多维矢量，再对矢量进行整体量化，就得到一种新的量化方法——矢量量化。矢量量化是标量量化的发展，凡是需要量化的地方都可以应用矢量量化。同时，矢量量化总是优于标量量化，矢量维数越大，矢量量化的性能就越优越。

20世纪70年代末，Linda、Buzo、Gray和Markel等首次解决了矢量量化码书生成的方法（称为LBG算法），并首先将矢量量化技术用于语音编码获得了巨大的成功。从此矢量量化技术不仅在语音压缩编码和语音识别等方面发挥了重要作用，而且很快推广到其他许多领域。目前，矢量量化不仅在理论研究上，而且在系统结构、计算机模拟及硬件实现等方面取得了大量的成果。

矢量量化的基本原理是将若干个标量数据组成一个矢量，在多维空间上整体量化，从而可以在信息量损失较小的情况下高效地压缩数据量。(www.xing528.com)

设有N个k维矢量X={x₁，x₂，…，x_N}（X⊂R^k，R为实数域（或欧氏空间）），其中

x_i={x₁，x₂，…，x_k}，i=1，2，…，N （5.64）

矢量x_i可以是随机波形信源{x（t）}的k个连续的样本值（即k维连续信源），或一帧连续信号中某种k个相关联的参数组成的矢量。再把k维欧氏空间R^k无遗漏地划分成n个互不相交的子空间R₁，R₂，…，R_n，在每一个子空间R_j中选取一个代表矢量y_j，n个代表矢量组成矢量集合：

Y={y₁，y₂，…，y_n} （5.65）

这样就组成了一个矢量量化器。在矢量量化中，Y称为码书（或码本），y_j称为码矢或码字，码书Y内矢量的个数n称为码书容量（或码书尺寸）。不同的划分或不同的代表矢量的选取方法构成不同的矢量量化器。

任意矢量x_i输入到矢量量化器并进行量化时，矢量量化器判断x_i属于哪个子空间R_j，然后输出该子空间R_j的代表矢量y_j。矢量量化的过程是将k维欧氏空间R^k中的矢量x_i映射到其有限子集Y的过程。

以k=2为例来说明矢量量化过程。记第i个二维矢量为x_i={x_i，1，x_i，2}，则所有可能的x_i={x_i，1，x_i，2}组成一个二维空间。二维矢量量化就是把这个平面划分为n块互不相交的子区域R₁，R₂，…，R_n，并从每一个子区域中选出一个代表矢量y_j（j=1，2，…，J），构成一个有n块区域的二维矢量量化器。图5.9是一个码书容量为7的二维矢量量化器，图中有7块区域和7个码字的代表值，码书是Y={y₁，y₂，…，y₇}。利用这个量化器对矢量x_i={x_i，1，x_i，2}量化时，首先要选择一个合适的失真测度，再根据最小失真原理，分别计算用各码矢y_j代替x_i所带来的失真。其中产生的失真最小时所对应的那个码矢，就是矢量x_i的重构矢量（或称恢复矢量），并称矢量x_i被量化成码矢y_j。

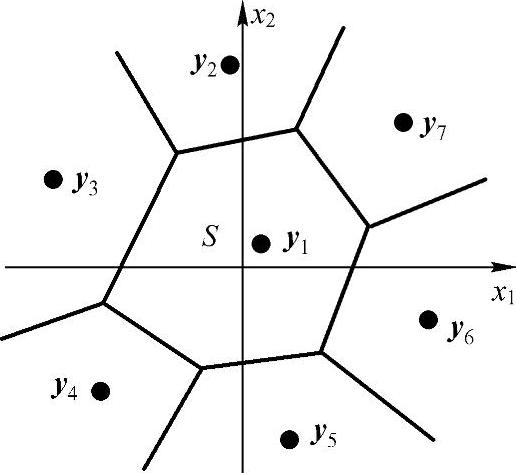
图5.9 二维矢量量化概念示意图

根据Shannon信息论，矢量维数越大，矢量量化性能越好。显然，矢量量化的过程与标量量化相似。在标量量化时，在一维的零至无穷大值之间设置若干个量化阶梯，当某输入信号的幅度值落在某相邻的两个量化阶梯之间时，就被量化为两阶梯的中心值。与此相对应，在矢量量化时，则将k维无限空间划分为n块区域边界，然后将输入矢量与这些边界进行比较，并被量化为“距离”最小的区域边界的中心矢量值。当然，矢量量化与标量量化一样，也会产生量化误差（即量化噪声），但只要码书容量足够大，量化误差就会足够小。另外，合理地选择码书也可以降低误差，这就是码书优化问题。

利用矢量量化技术时主要有两个问题要解决：

1）设计一个好的码书。好的码书有两个标志，即n个区域边界和代表码字。划分n个区域边界需要用大量的输入信号矢量，经过统计实验才能确定。这个过程称为“训练”或“学习”，其任务是建立码书。按照一定的失真度准则，应用聚类算法对训练数据进行分类，从而把训练数据在多维空间中划分成一个个以质心（码字）为中心的子空间，常用LBG算法来实现。为了建立一个好的码书，不仅要求建立码书的训练数据的量要充分大，而且要有代表性；其次，要选择一个好的失真准则以及码书优化方法。

2）未知矢量的量化。按照选定的失真测度准则，把未知矢量量化为失真测度最小的区域边界的中心矢量值（码字矢量），并获得该码字的序列号（码字在码书中的地址或编号）。同样存在两矢量在进行比较时的测度问题。这个测度就是两矢量之间的距离，或以其中某一矢量为基准时的失真度。它描述了当输入矢量用码书中对应的码矢来表征时所应付出的代价。其次是未知矢量量化时的搜索策略，好的搜索策略可以减少量化时间。

矢量量化器的最佳码书设计就是：

1）从大量的信号样本中训练出优化的码书。

2）从实际效果出发寻找到好的失真测度。

3）用最少的搜索和计算失真的运算量实现最大可能的平均信噪比。

如果用d（x，y）表示训练用特征矢量x与训练出的码书的码字y之间的畸变（失真测度），则最佳码书设计的任务就是在一定条件下，使得此畸变的统计平均值D=E[d（x，y）]最小。为了实现这一目的，应该遵循以下两条原则：

1）根据x选择相应的码字y_j时遵从最近邻准则（Nearest Neighbor Rule，NNR）：

2）设S_l是所有选择码字y_l（即归属于y_l所表示的区域）的输入矢量x的集合，那么y_l应使此集合中的所有矢量与y_l之间的畸变值最小。如果x与y之间的畸变值等于它们的欧氏距离，那么容易证明y_l应等于S_l中所有矢量的质心，即

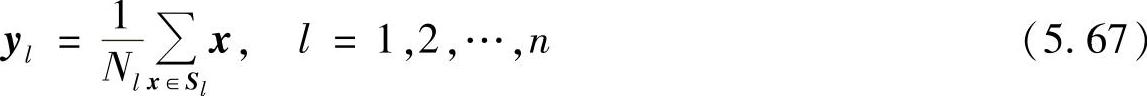
式中，N_l是集合S_l中矢量的个数。

根据上述两条原则可以设计出计算码书的递推算法。算法的核心实际上是上述两个条件的反复迭代过程，即从初始码书寻找最佳码书的迭代过程。它由对初始码书进行迭代优化开始，直到系统性能满足要求或不再有明显的改进为止。

下面给出LBG算法的具体实现步骤：

1）设定码书和迭代训练参数：全部输入的训练矢量x的集合为S，码书的容量为n，最大迭代次数为L，两个矢量的最小畸变阈值为δ。

2）初始化：n个码字初值为y₁^（0），y₂^（0），…，y_n^（0），畸变初值D（0）=∞，迭代次数初值m=1。

3）将S分成n个子集S₁^（m），S₂^（m），…，S_n^（m）：根据最近邻准则，对每一个x∈S，若有d（x，y_l^（m-1））≤d（x，y_i^（m-1））（i=1，2，…，n；i≠l），判定x∈S_l^（m）。

4）计算总畸变。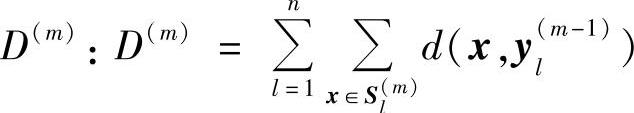

5）计算畸变改进量ΔD^（m）的相对值δ^（m）：。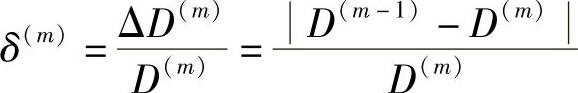

6）更新码书的码字y₁^（m），y₂^（m），…，y_n^（m）：y。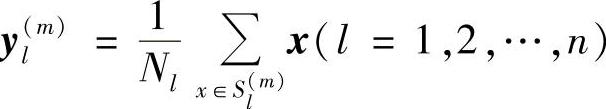

7）若满足δ^（m）＜δ，则转入9）执行；否则，转入8）执行。

8）若满足m≥L，则转入9）执行；否则，令m=m+1，转入3）执行。

9）迭代终止；输出优化的最佳码书。