限失真信源编码定理的应用及意义

本节给出信息率失真理论的基本定理。这些定理严格地证实了R（D）函数确实是在允许失真为D条件下，每个信源符号能够被压缩的最低值。虽然，本节的讨论限于离散无记忆平稳信源，但所述定理可以推广到连续信源、有记忆信源等更一般的情况。

定理5.3 设离散无记忆平稳信源的信息率失真函数为R（D），只要使信息传输率R满足R＞R（D），并且失真度是有限的，当信源序列长度n足够长时，一定存在一种编码方法，其译码失真≤D+δ，其中δ是任意小的正数；反之，若R＜R（D），则无论采用什么样的编码方法，其译码失真必大于D。

该定理称为Shannon第三编码定理，它包含两部分：R＞R（D）的情况称为正定理，R＜R（D）的情况称为逆定理。通过正、逆定理说明R（D）是限失真信源编码的界。该定理与Shannon第二编码定理（即有噪信道编码定理，见第6章）一样，只是码的存在性定理。

正定理表明，R＞R（D）时，译码失真≤D+ε的编码肯定存在，但定理本身并未告知码的具体构造方法。一般来说，要找到满足条件的编码，只能用优化的思路去寻找。迄今尚无合适的系统编码方法来接近Shannon给出的界R（D）。

逆定理表明，R＜R（D）时，译码失真必大于D，肯定找不到满足条件的码。因此，用不着浪费时间和精力。

下面将正定理和逆定理分别转换为严格的数学形式。

定理5.4（限失真信源编码正定理） 设离散无记忆平稳信源的信息率失真函数为R（D），且失真度是有限的。对于任意的D≥0，ε＞0，δ＞0，以及任意足够长的码长n，则一定存在一种信源编码C，其码字个数为

M=h^{n[R（D）+ε]}（5.57）

而编码后的平均失真度d（C）≤D+δ，其中，R（D）以h为底，h为编码进制数。

如果用二元编码，且R（D）计算以2为底，即以bit为单位，则M=2^{n[R（D）+ε]}。

定理5.4表明，对于任何失真度D≥0，只要码长n足够长，总可以找到一种信源编码C，使编码后的每个信源符号的信息传输率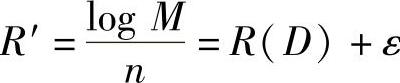ε。即R′≥R（D），而码的平均失真度d（C）≤D。这说明在允许失真D条件下，信源最小的、可达到的信息传输率是信源的信息率失真函数R（D）。

定理5.5（限失真信源编码逆定理） 不存在平均失真度为D、平均信息传输率R′＜R（D）的任何信源编码。即对任意码长n的信源编码，若码字个数M＜h^nR（D），一定有d（C）＞D。

定理5.5表明，如果编码后平均每个信源符号的信息传输率R′＜R（D），就不能在保真度准则下再现信源的消息，即失真必然超过D。

定理5.4和定理5.5的完整证明请参考文献[14]。(www.xing528.com)

从Shannon第三编码定理可知，R（D）确实是允许失真度为D的情况下信源信息压缩的下限值。比较Shannon第一编码定理和第三编码定理可知，当信源给定后，无失真信源压缩的极限值是信源熵H（X），而有失真信源压缩的极限值是信息率失真函数R（D）。在给定某个D值之后，一般R（D）＜H（X）。

无失真信源编码可以看成是限失真信源编码的特例。根据对失真的正常的定义，一般当输入和输出符号一一对应时，失真才为0，此时R（0）=H（X）。可以通过限失真信源编码定理来证明无失真信源编码定理。

类似于无失真信源编码利用信源熵来衡量编码的效率一样，信息率失真函数R（D）可以用来度量限失真信源编码在某一失真下的信源编码的效率。

在实际应用中，主要存在以下三类运用Shannon第三编码定理的问题：

第一类问题是，符合实际信源的R（D）函数的计算相当困难。

1）需要对实际信源的统计特性有确切的数学描述，即概率分布明确。

2）需要对符合主观和客观实际的失真给予正确的度量，否则不能求得符合主观和客观实际的R（D）函数。

例如，通常采用均方误差来表示信源的平均失真度，但对于图像信源来说，均方误差较小的编码方法在人们的视觉中失真较大，所以，人们常采用主观观察来评价编码方法的好坏。因此，如何定义符合主观和客观实际情况的失真测度，就是件较困难的事。

3）即便对实际信源有了确切的数学描述，又有符合主观和客观实际情况的失真测度，而失真函数的计算仍然较困难。

第二类问题是，即便求得了符合实际的R（D）函数，还需要研究采取何种实用的最佳编码方法才能达到极限值R（D）。

目前，这两方面工作都有进展，尤其是对实际信源的各种压缩方法，如对语音信号、图像信号、视频信号和遥感图像等信源的各种压缩方法有了巨大进步。

第三类问题是，R（D）的求解是在给定试验信道的输入/输出及其失真矩阵的情况下计算的。当输出的符号集未定时，不能确定到底什么样的符号集才是最优的，即使R（D）最小。

在人类社会进入信息时代以来，多媒体计算机、多媒体数据库、多媒体通信和多媒体表现技术等多媒体研究领域成为计算科学和通信技术发展中的一个重要研究热点。其中，面临的最大问题是巨大数据量的“爆炸”。文件、表格和工程图纸（二值图像）等的数据已较大。但相比之下，语音信号、静止灰度图像信号、彩色静止图像信号、电视图像和高清电视图像等的数据量更是巨大。因此，研究有效的数据压缩和解压缩的技术成为重要的、关键的研究方向。而信息率失真理论正是从理论上指出这种问题的解决的途径是存在的、可能的。