计算信息率失真函数的信源对称性优化方案

通常一个具有对称性的数学优化问题，其极值（极大或极小值）解也出现在某种对称点上。因此，对于这类具有对称性的问题就可以利用对称性求得最优解。下面通过例子说明利用信源的对称性计算R（D）函数。

【例5.7】

设信源为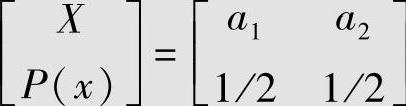，输出符号集为Y，其值域为B：{b₁，b₂，b₃}。失真矩阵为

求信息率失真函数R（D）。

解1）确定R（D）的定义域。由式（5.20）和式（5.21）分别计算D_min和D_max如下：

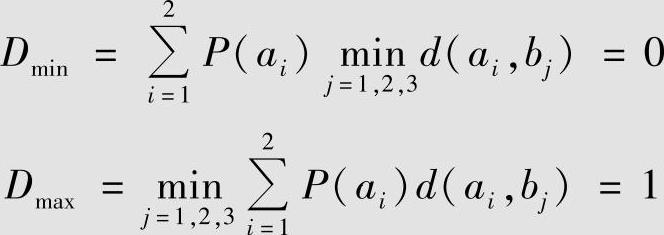
2）确定转移概率P（b_j|a_i）。由于信源X等概率分布、失真函数具有对称性，因此存在与失真函数具有类似对称性的转移概率达到R（D）函数，设该转移概率矩阵为

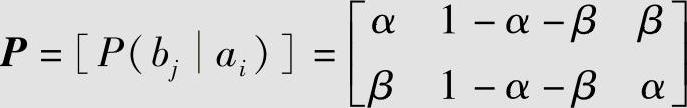
因为d（a₁，b₃）=d（a₂，b₁）=∞，所以对于任何有限平均失真，必须β=0。

3）确定转移概率P（b_j|a_i）与失真度D的关系。由式（5.6）计算平均失真度为

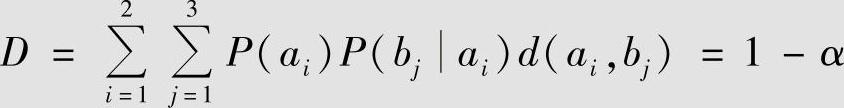
因此，α=1-D，允许失真为D的试验信道为

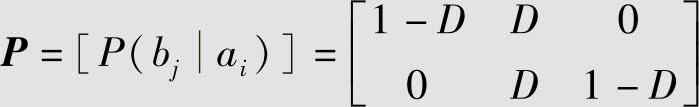
4）计算输出符号的概率为P（b₁）=P（b₃）=（1-D）/2，P（b₂）=D。

5）计算信息率失真函数：

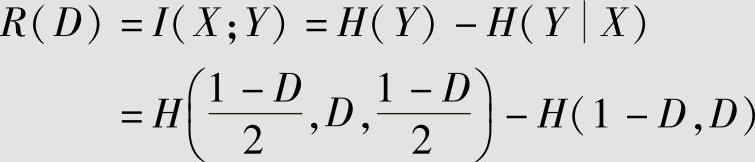
即

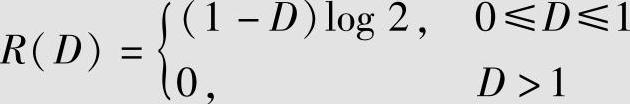
相应的信息率失真函数R（D）如图5.4所示。

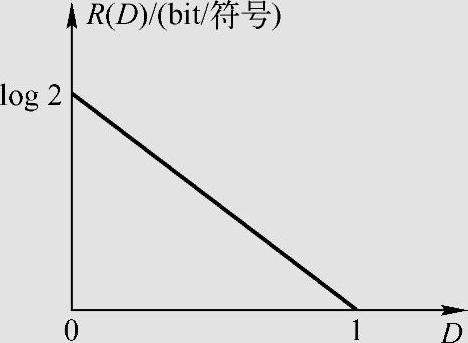
图5.4 二元等概信源R（D）函数曲线

【例5.8】(www.xing528.com)

设X是r元等概信源，其值域为A：{a₁，a₂，…，a_r}；输出符号集为Y，其值域为B：{b₁，b₂，…，b_r}；求Hamming失真度时的信息率失真函数R（D）。

解1）依题意，信源概率分布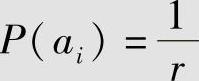：，i=1，2，…，r

Hamming失真度：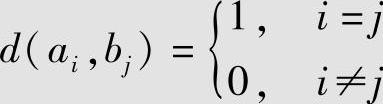

2）确定R（D）的定义域。由式（5.20）和式（5.21）分别计算D_min和D_max如下：

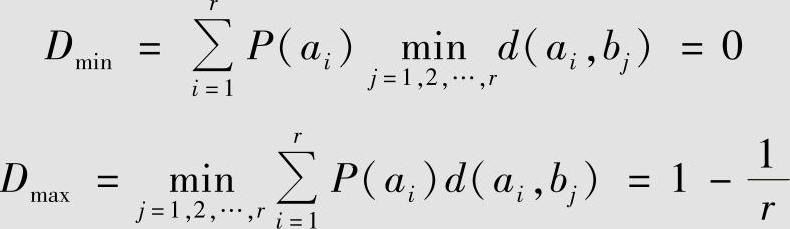
3）确定转移概率P（b_j|a_i）。由于信源等概率分布、Hamming失真函数具有对称性，因此存在与失真函数具有类似对称性的转移概率达到R（D）函数，设该转移概率为

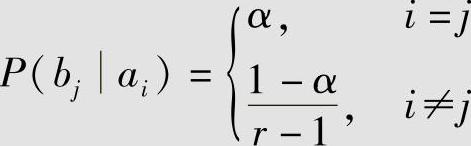
4）确定转移概率P（b_j|a_i）与失真度D的关系。由式（5.6）计算平均失真度为

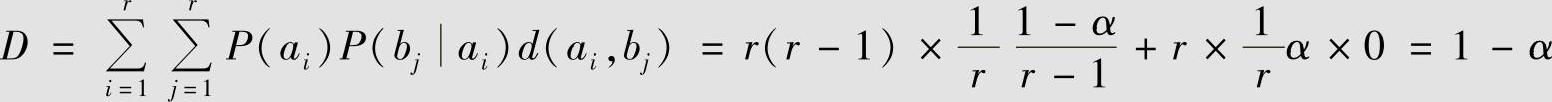
因此，α=1-D，允许失真为D的试验信道为

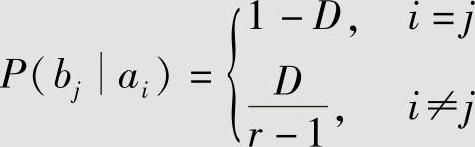
5）计算输出符号的概率：

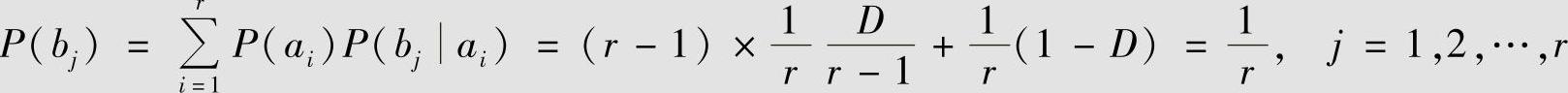
6）计算信息率失真函数：

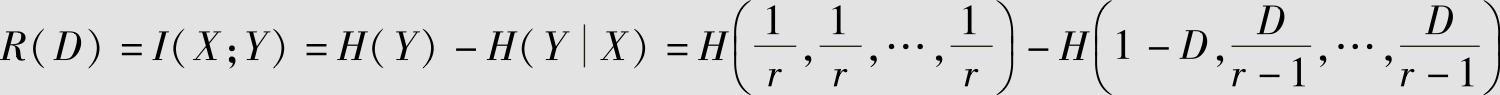
即

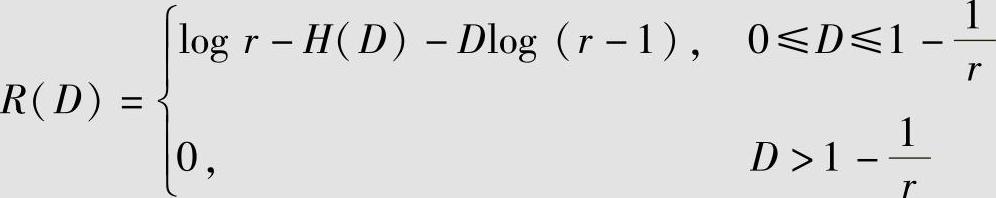
相应的信息率失真函数R（D）如图5.5所示。

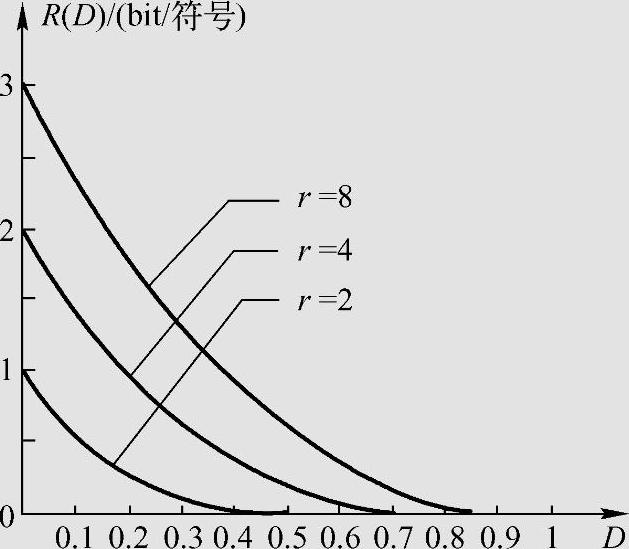
图5.5 r元等概信源R（D）函数曲线

从图5.5可知，对于相同的平均失真度D，r越大，R（D）越大，信源压缩性越小。若把r的取值看成是连续信源分层后的符号数，即r越大就表示信源分层越多。于是，在满足相同的允许失真要求下，分层越多，信源的可压缩性就越小；反之，分层越少，信源的可压缩性就越大。这些规律对于实际信源的量化分层、数据压缩有深刻的指导意义。