信息率失真函数性质分析

性质5.1 信息率失真函数R（D）的定义域为0≤D_min≤D≤D_max，D＜D_min时R（D）无意义；D＞D_max时，R（D）=0；且

证明1）首先证明下界式（5.20）。根据定义式（5.6），可进行如下推导：

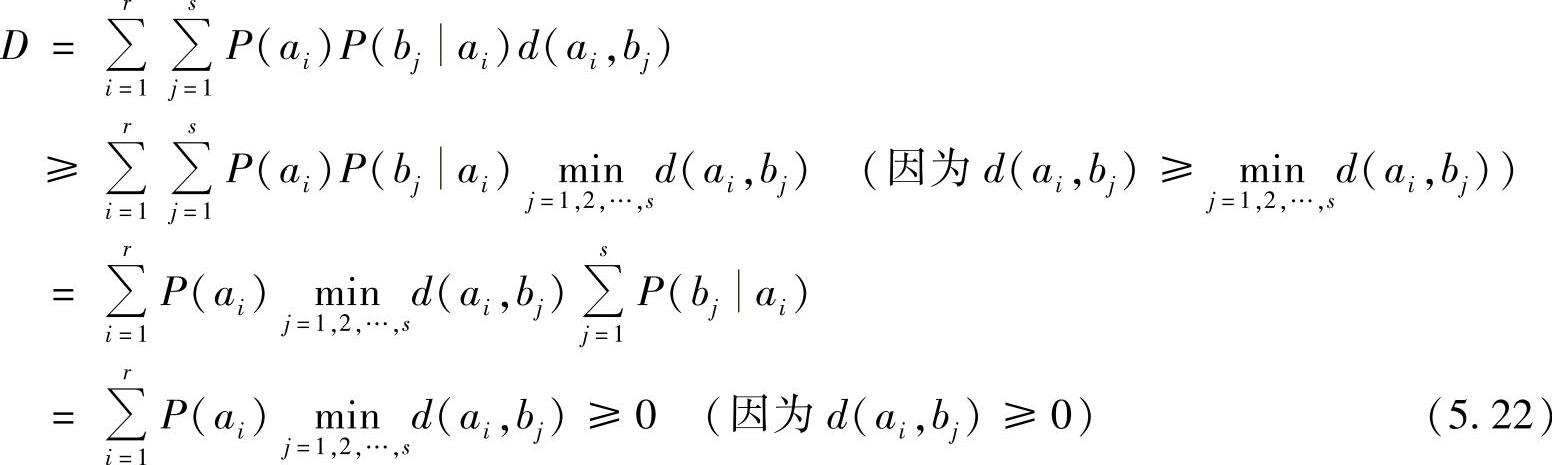
又因为d（a_i，b_j）≥0，故D不可能小于0。因此，D＜0时R（D）也就无意义了。

选择试验信道，对于每一个a_i，令对应最小的d（a_i，b_j）的条件概率P（b_j|a_i）=1，其余条件概率为0，即得到D_min，即取

将式（5.23）代入式（5.22），则得到可能的最小平均失真度D_min的表达式，即式（5.20）成立，且D＜D_min时R（D）也是无意义的。

2）下面证明上界式（5.21）。

因为R（D）是平均互信息，所以R（D）≥0。

因为在较大范围内的极小值一定不大于在所含的小范围内的极小值，所以，D₁≥D₂⇒R（D₁）≤R（D₂），即R（D）是平均失真度D的非增函数。

当D增大时，R（D）可能减小，直到减小到R（D）=0。此时对应着D_max。当D再增大时R（D）仍然为0。D_max是使R（D）=0的平均最小失真度。

因为X和Y相互独立，即P（a_ib_j）=P（a_i）P（b_j），使得R（D）=0。所以

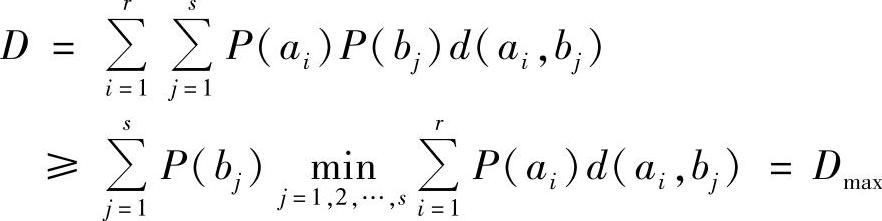
由于P（a_i）和d（a_i，b_j）已给定，而且对于不同的b_j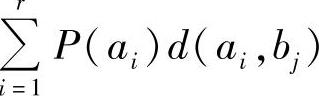，也可以有不同的值。所以，求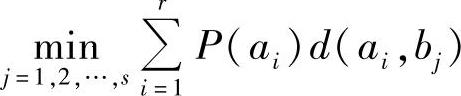，并使对应的P（b_j）=1，其余为0。这样就可以使平均失真度最小。最终证得式（5.21）。

【证毕】

由式（5.20）可知，只有当失真矩阵中每行至少有一个零元素时，信源的平均失真度才能达到下限值0，否则D_min＞0。在实际情况中，一般D_min=0，它表示信源不允许任何失真存在。直观地理解，这时信息率至少应等于信源熵，即R（0）=H（X）。

可以证明，只有当失真矩阵中每行至少有一个零元素，并且每列最多只有一个零元素时，式R（0）=H（X）成立。

但是当失真矩阵除了满足D_min=0的条件，即每行至少有一个零元素以外，某些列还有不止一个0时，说明信源符号集有些符号可以压缩、合并而不带来任何失真，压缩后的信息率必然减小，这时R（0）＜H（X）。

【例5.5】（续例5.3）

求例5.3中信源的最小允许失真度。由式（5.20）可知

满足最小允许失真度的试验信道是一个无噪无损的试验信道，信道转移概率矩阵为

可以看出，若取允许失真度D=D_min=0，则B_D集合中只有这个信道是唯一可取的试验信道，也就是无失真一一对应的编码。因此，有I（X；Y）=H（X），而无失真时的信息率失真函数为

【例5.6】

设信源为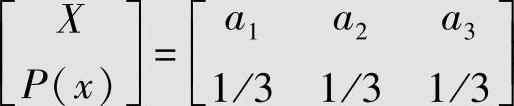，信宿Y的值域为B：{b₁，b₂}。失真矩阵为

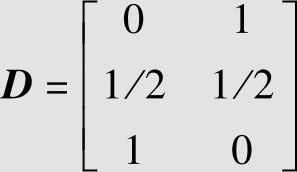
由式（5.20）可知

由式（5.23）可知，使平均失真度达到最小值（D=1/6）的信道必须满足

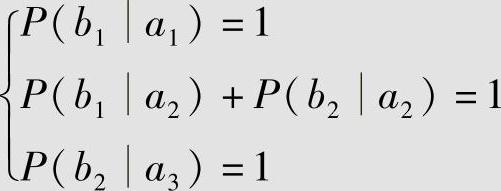
因为P（b₁|a₂）+P（b₂|a₂）=1的限制，P（b₁|a₂）和P（b₂|a₂）有无穷多组解，且它们的最小平均失真度都是1/6，即集合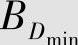中的信道有无穷多个。这些信道的共同特征是当已知接收符号b_j（j=1，2）时不能唯一确定发送符号a_i（i=1，2，3），所以其信道疑义度H（X|Y）≠0，则得

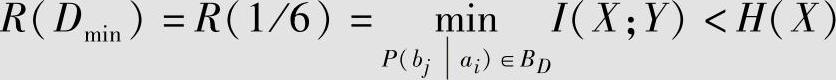
性质5.2 信息率失真函数R（D）是关于平均失真度D的∪形凸函数（又称下凸函数），即设D₁和D₂是两个任意平均失真度，取0＜θ＜1和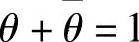，则

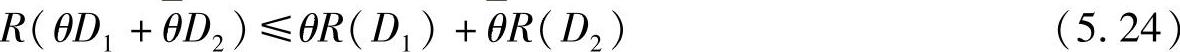
证明根据∪形函数的定义来进行证明。(www.xing528.com)

当信源概率分布给定后，R（D）可以看作是信道转移概率P（y|x）的函数，即

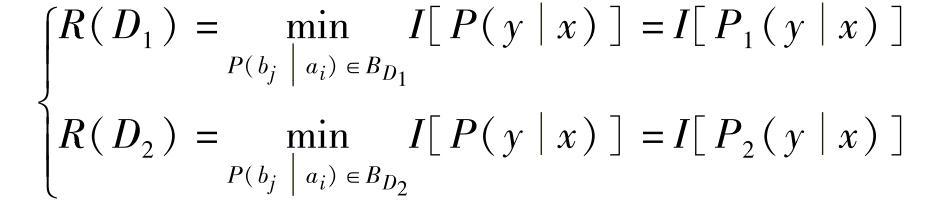
且有

现令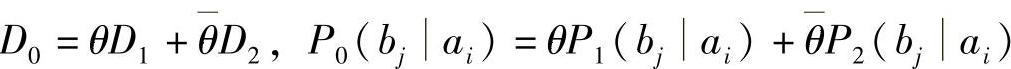，则有

可知，P₀（b_j|a_i）满足保真度准则D₀，即P₀（b_j|a_i）∈B_D0。

【证毕】

性质5.3 信息率失真函数R（D）是（D_min，D_max）区间上的连续和严格单调递减函数。

证明 由性质5.2知R（D）是下凸函数，因此R（D）在（D_min，D_max）区间上是连续的。

由D₂＞D₁⇒B_D2⊃B_D1，而在较大范围内的极小值一定不大于在所含的小范围内的极小值，所以R（D₁）≥R（D₂）。下面用反证法证明在（D_min，D_max）区间上R（D）是严格单调递减函数。

设区间[D₁，D₂]，且有D_min＜D₁＜D₂＜D_max。如果假定在该区间上R（D）为常数，则R（D）就不是严格递减的，现证明此假设不能成立。

现有两个试验信道P₁（b_j|a_i）和P₀（b_j|a_i），它们达到对应的信息率失真函数分别为R（D₁）和R（D_max）。则有

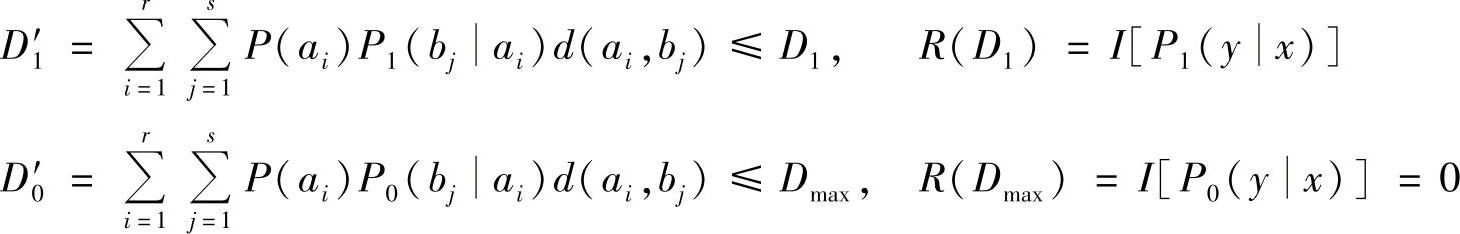
对于足够小的θ，总能找到θ＞0，使满足D₁＜θD_max+θD₁＜D₂。现在定义一个新的试验信道，设其信道转移概率为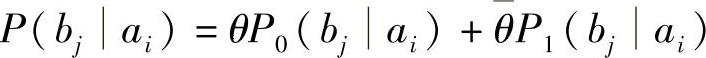，再设允许的平均失真度为D=θD_max+θD₁，则

D₁＜D＜D₂ （5.25）

对应于新试验信道的平均失真度为

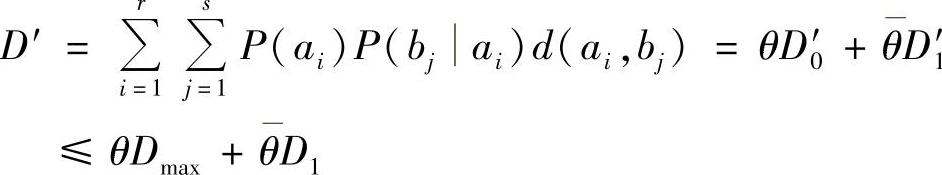
可见，新试验信道满足保真度准则，但它不一定是达到信息率失真函数的试验信道，故一般有

R（D）≤I（X；Y） （5.26）

由平均互信息对信道转移概率特性P（b_j|a_i）的下凸性，有

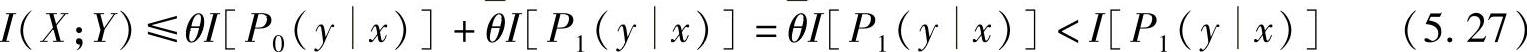
综合式（5.25）～式（5.27）可知，当D＞D₁时，R（D）＜R（D₁）。即在区间[D₁，D₂]内，R（D）不为常数。这与初始假设矛盾，因而，R（D）是严格递减的。

【证毕】

根据以上几点性质，可以大体画出一般信源（无记忆、有记忆）信息率失真函数R（D）的典型曲线图，如图5.3所示。图5.3a中设D_min=0，而图5.3b中设D_min≠0。图中R（D_min）和R（D_max）决定了曲线的两个端点，R（D_min）≤H（X），R（D_max）=0；在D_min和D_max之间R（D）是单调递减的下凸函数。在连续信源的情况下，当D→0时R（0）→∞，曲线不与纵轴相交，如图中虚线所示。

关于信息率失真函数的两点解释如下：

1）通常总是希望信息通过信道传输时，输入与输出之间的互信息最大，这是在信道给定情况下的要求。而这里是指在信源给定而不是信道给定的传输。信息率失真理论要解决的问题就是计算满足失真要求的传输所需要的最小信道容量或信息传输率，以达到降低信道的复杂度和通信成本的目的。

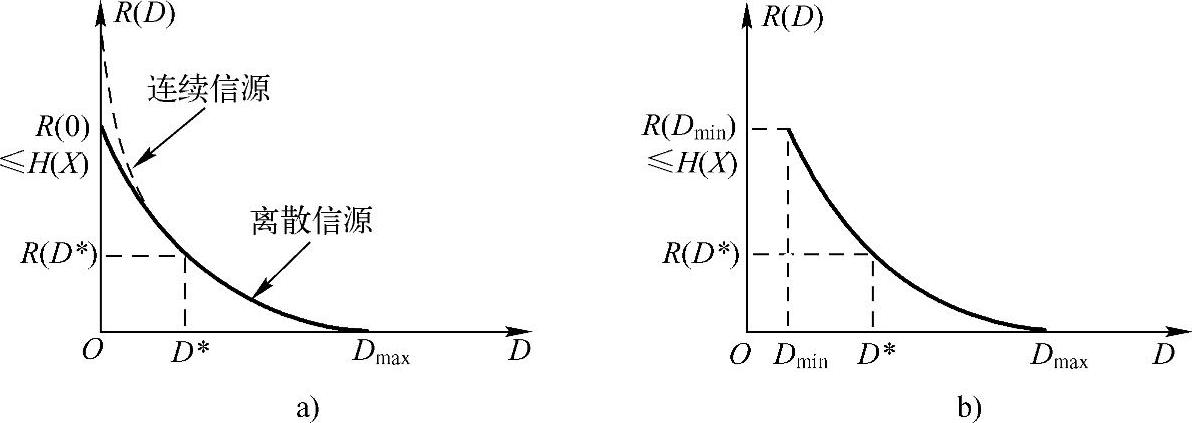
图5.3 R（D）函数的典型曲线

a）D_min=0时R（D）曲线 b）D_min≠0时R（D）曲线

2）根据R（D）为单调减函数的性质，如果固定平均互信息，选择信道的转移概率使平均失真最小，可以得到类似R（D）的函数。其差别是变量之间作用交换，成为D（R）的函数。这时就得到了失真率函数（Distortion-Rate Function）。

失真率函数定义为

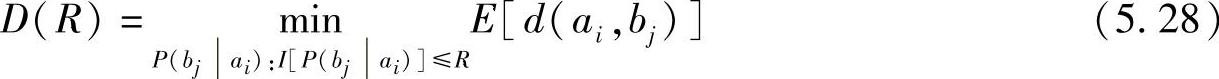
使用这种定义意味着既给定了信源，又给定了信道容量。问题是寻找达到平均失真最小的理想信道。这种定义好像比求最小互信息更自然，同时更有助于说明信息率失真理论是用来对有失真系统的性能进行比较的标准。

实际上在某些情况下，使用失真率函数比较方便；而在其他一些情况下，使用信息率失真函数比较方便。应习惯这两种定义的使用。