定义信息率失真函数

由前面的分析，通过假想试验信道的引入，把有失真信源编码问题转化为无失真的信源通过有噪信道传输的问题，进而通过研究试验信道输入与输出之间的互信息来研究限失真信源编码。下面就从互信息出发引入信息率失真函数。

定义5.9 满足保真度准则的信道称为许可试验信道，所有许可试验信道的集合用B_D表示，对于离散单符号信源和信道，有

对于离散无记忆N次扩展信源和信道，有

定义5.10 在满足保真度准则的许可试验信道的集合B_D中，平均互信息的最小值定义为信息率失真函数R（D），简称率失真函数，其表达式为

信息率失真函数的单位与平均互信息的单位相同。

对于N次扩展信源，当信源和信道均为无记忆时，I（X；Y）=NI（X；Y），所以有

R_N（D）=NR（D） （5.19）它是在所有满足平均失真度D′（N）≤ND的N维试验信道集合B_D（N）中，寻找某个信道使I（X；Y）取极小值。因为平均失真度D′（N）与长度N有关，所以，在其他条件（信源概率分布、单个符号的失真度）相同的条件下，对于不同的N，R_N（D）是不同的。

对于给定的信源，在满足保真度准则D′≤D的前提下，信息率失真函数R（D）是信源输出的信息率允许压缩到的最小值。由于I（X；Y）是P（b_ja_i）的下凸函数，所以在B_D集合中，I（X；Y）的最小值一定存在。

从数学上来看，平均互信息I（X；Y）既是信源概率分布P（a_i）的上凸函数，又是信道转移概率P（b_ja_i）的下凸函数，因此信道容量C和信息率失真函数R（D）具有对偶性。(www.xing528.com)

信道容量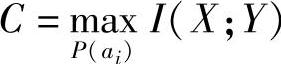是指在信道固定前提下，选择一种信源概率分布使信息传输率最大（求极大值）。它反映了信道传输信息的能力，是信道可靠传输的最大信息传输率。

信息率失真函数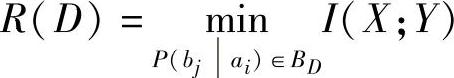是在信源固定，满足保真度准则D′≤D条件下的信息传输率的最小值。它反映了满足给定失真度条件下信源可以压缩的程度，也就是满足失真要求而再现信源消息所必须获得的最少平均信息量。

因此可以得出结论：

1）信道容量与信源无关，是信道特性的参量，不同的信道其信道容量不同。

2）信息率失真函数与信道无关，是信源特性的参量，不同的信源其信息率失真函数不同。

这两个概念的适用范围是不一样的，研究信道容量C是为了在已知信道中尽可能多地传输信息，充分利用已给定的信道，使传输的信息量最大，错误概率任意小，以提高通信的可靠性。这是信道编码问题。

研究信息率失真函数是为了在已知信源和允许失真度条件下，使信源输出的信息率尽可能小，也就是在允许的给定失真度条件下，使信源必须传输给信宿的信息量最少，尽可能用最少的码符号来传输信源信息，使信源的信息可以尽快地传输出去，以提高通信的有效性。这是信源编码问题。